1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm

2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực

1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm

2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực

Tham Khao :

1. 

a. Định nghĩa: Hai phương trình gọi là tương đương nếu chúng có cùng một tập hợp nghiệm.

b. Hai quy tắc biến đổi tương đương các phương trình: 

2.

Phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn. Ví dụ: Phương trình 5x – 2 = 0 là phương trình bậc nhất ẩn x. Phương trình y – 8 = 4 là phương trình bậc nhất ẩn y.

3.

Để giải các phương trình đưa được về ax+b=0 a x + b = 0 ta thường biến đổi phương trình như sau: + Quy đồng mẫu hai vế và khử mẫu. + Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax+b=0 a x + b = 0 hoặc ax=−b a x = − b .

Phương trình A là phương trình bậc hai một ẩn vì a<>0

\(\sqrt{2}t^2-2t+4=0\)

\(\text{Δ}=\left(-2\right)^2-4\cdot\sqrt{2}\cdot4=4-16\sqrt{2}< 0\)

Do đó; Phương trình vô nghiệm

Em là học sinh lớp 7 nên em giải theo cách hiểu của em nhé: 

a)* Định nghĩa 

Phương trình ax + b = 0, với a và b là hai số đã cho và a # 0 được gọi là phương trình bậc nhất một ẩn

* Cách giải:

Bước 1: Chuyển vế ax = -b

Bước 2: Chia hai vế cho a: x = \(\frac{-b}{a}\)

Bước 3: Kết luận nghiệm: S = \(\frac{-b}{a}\)

Ta có thể trình bày ngắn gọn như sau:

ax + b = 0 <=> ax = -b <=> x = \(\frac{-b}{a}\)

Vậy tập nghiệm của phương trình là S = \(\left\{\frac{-b}{a}\right\}\)

b) Nếu giải theo mô hình trên, ta có:

\(A=2x+4=0\\ \Leftrightarrow2x=-4\\ \Leftrightarrow x=\frac{-4}{2}\\ \Leftrightarrow x=-2\)

Vậy tập nghiệm của phường trình A là: {-2}

Chúc chị học tốt!

Mày nhìn cái chóa j

4 x 2  – 12x + 5 = 0 ⇔ 4 x 2  – 2x – 10x + 5 = 0

⇔ 2x(2x – 1) – 5(2x – 1) = 0 ⇔ (2x – 1)(2x – 5) = 0

⇔ 2x – 1 = 0 hoặc 2x – 5 = 0

       2x – 1 = 0 ⇔ x = 0,5

       2x – 5 = 0 ⇔ x = 2,5

Vậy phương trình có nghiệm x = 0,5 hoặc x = 2,5

Đề bài đâu

KO dùng máy tính CASINO là sao để giải phương trình bậc 4 tính ra giấy gãy tay có đó

bạn đưa bài ra đi ms giải đc chứ

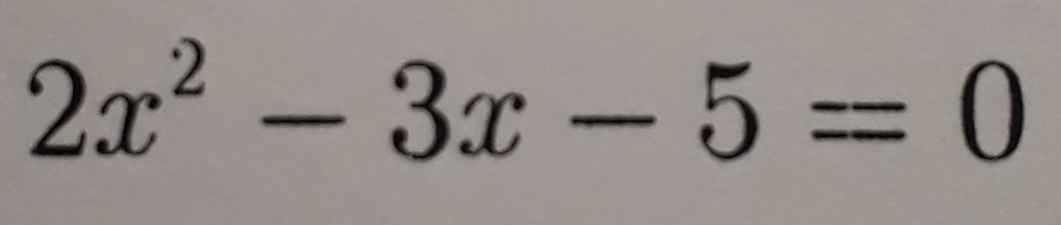
\(2x^2-3x-5=0 \\ \Leftrightarrow2x^2+2x-5x-5=0\\ \Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\\ \Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5\\x=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\\ Vậy.S=\left\{\dfrac{5}{2};-1\right\}\)

\(2x^2-3x-5=0\)

\(\Leftrightarrow2x^2+2x-5x-5=0\)

\(\Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\)

\(\Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\)

Vậy \(x=\dfrac{5}{2};x=-1\) là các nghiệm của phương trình.

#\(Toru\)

a) Cách giải các phương trình lượng giác cơ bản:

+ Phương trình sin x = a.

Nếu |a| > 1 ⇒ phương trình vô nghiệm.

Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.

Khi đó phương trình trở thành sin x = sin α

⇒ Phương trình có nghiệm: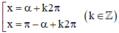 

+ Phương trình cos x = a.

Nếu |a| > 1 ⇒ phương trình vô nghiệm.

Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.

Khi đó phương trình trở thành cos x = cos α.

⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).

+ Phương trình tan x = a.

Tìm một cung α sao cho tan α = a.

Khi đó phương trình trở thành tan x = tan α.

⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).

+ Phương trình cot x = a

Tìm một cung α sao cho cot α = a.

Khi đó phương trình trở thành cot x = cot α.

⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).

b) Cách giải phương trình a.sin x + b.cos x = c.

+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .

+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho  ta được:

Ta giải phương trình trên như phương trình lượng giác cơ bản.