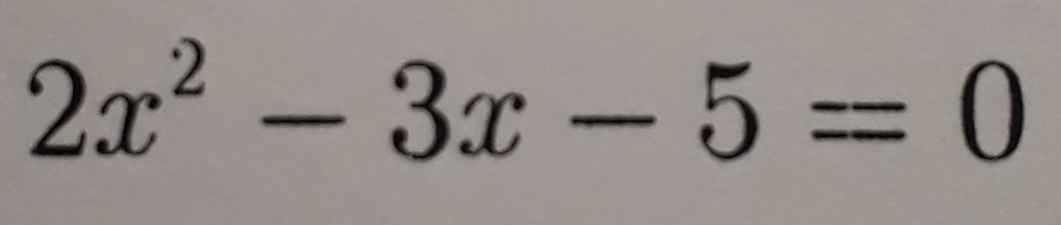\(2x^2-3x-5=0 \\ \Leftrightarrow2x^2+2x-5x-5=0\\ \Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\\ \Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5\\x=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\\ Vậy.S=\left\{\dfrac{5}{2};-1\right\}\)
\(2x^2-3x-5=0\)
\(\Leftrightarrow2x^2+2x-5x-5=0\)
\(\Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\)
Vậy \(x=\dfrac{5}{2};x=-1\) là các nghiệm của phương trình.
#\(Toru\)