a: BC=10cm

C=AB+BC+AC=6+8+10=24(cm)

b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔABD=ΔHBD

c: Ta có: ΔABD=ΔHBD

nên DA=DH

mà DH<DC

nên DA<DC

ΔABC vuông tại A

=>BC^2=AB^2+AC^2

=>BC^2=6^2+8^2=100

=>BC=10(cm)

Xét ΔBAC có BD là phân giác

nên DA/AB=DC/BC

=>DA/3=DC/5

=>\(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=1\)

=>DC=5(cm)

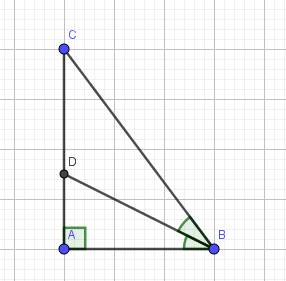
\(\Delta ABC\) vuông tại A

\(\Rightarrow BC^2=AB^2+AC^2\) (Pytago)

\(=6^2+8^2\)

\(=100\)

\(\Rightarrow BC=10\left(cm\right)\)

Do BD là tia phân giác của \(\widehat{ABC}\)

\(\Rightarrow\dfrac{AB}{AD}=\dfrac{BC}{DC}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{AB}{AD}=\dfrac{BC}{DC}=\dfrac{AB+BC}{AD+DC}=\dfrac{6+10}{8}=2\)

\(\dfrac{BC}{DC}=2\Rightarrow DC=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)

\(BC^2=AB^2+AC^2=36+64=100\left(Pitago\right)\)

\(\Rightarrow BC=10\left(cm\right)\)

Áp dụng tính chất phân giác của tam giác ABC :

\(\dfrac{AB}{BC}=\dfrac{AD}{CD}\)

\(\Rightarrow\dfrac{AB}{AD}=\dfrac{BC}{CD}=\dfrac{AB+BC}{AD+CD}=\dfrac{AB+BC}{BC}=\dfrac{6+10}{10}=\dfrac{16}{10}=\dfrac{8}{5}\)

\(\Rightarrow CD=\dfrac{5}{8}.BC=\dfrac{5}{8}.10=\dfrac{25}{4}\left(cm\right)=6,25\left(cm\right)\)

a. Áp dụng định lý pitago, ta có:

\(BC^2=AB^2+AC^2\)

\(\Rightarrow AC=\sqrt{10^2-6^2}=\sqrt{64}=8cm\)

\(C_{ABC}=6+8+10=24cm\)

b. xét tam giác vuông ABD và tam giác vuông BDM, có:

B : góc chung

AD: cạnh chung

Vậy  tam giác vuông ABD = tam giác vuông BDM ( cạnh huyền - góc nhọn )

có vẽ hình nha mọi người

Bài 1:

a) Ta có:

\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)

\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)  

b) Áp dụng Py-ta-go ta có: 

\(BC^2=AB^2+AC^2=6^2+15^2=261\)

\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)

Bài 2: 

\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)

1: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=6^2+8^2=100\)

=>BC=10(cm)
XétΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)

nên \(\widehat{C}\simeq37^0\)

ΔABC vuông tại A

=>\(\widehat{B}+\widehat{C}=90^0\)

=>\(\widehat{B}+37^0=90^0\)

=>\(\widehat{B}=53^0\)

2: Xét tứ giác AEKF có

\(\widehat{AEK}=\widehat{AFK}=\widehat{FAE}=90^0\)

=>AEKF là hình chữ nhật

=>AK=EF và AK cắt EF tại trung điểm của mỗi đường

=>I là trung điểm chung của AK và EF và AK=EF

\(IA=IK=\dfrac{AK}{2}\)

\(IE=IF=\dfrac{EF}{2}\)

mà AK=EF

nên IA=IK=IE=IF=AK/2

=>\(IE\cdot IF=\dfrac{1}{2}\cdot AK\cdot\dfrac{1}{2}\cdot AK=\dfrac{1}{4}\cdot AK^2\)

=>\(4\cdot EI\cdot IF=AK^2\left(1\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(BK\cdot KC=AK^2\left(2\right)\)

Từ (1) và (2) suy ra \(4\cdot EI\cdot IF=BK\cdot KC\)

tam giác abc ạ. E cần gấp

A) Xét   \(\Delta HBA\) và  \(\Delta ABC\) có :

\(\widehat{B}\) chung     ;     \(\widehat{BAC}=\widehat{BHA}=90\)  độ

\(\Leftrightarrow\Delta HBA\infty\Delta ABC\left(g.g\right)\)

B)  Xét \(\Delta ABE\) và \(\Delta ACB\) có : 

       \(\widehat{A}\)   chung

      \(\widehat{ABE}=\widehat{BCA}\)( Do BE là phân giác của góc B , mà   \(\widehat{B}=2\widehat{C}\))

\(\Leftrightarrow\Delta ABE\infty\Delta ACB\left(g.g\right)\)

Ta có tỉ lệ :  \(\frac{AB}{AC}=\frac{AE}{AB}\)\(\Leftrightarrow AB^2=AE\cdot AC\left(dpcm\right)\)

C)  ta có tỉ lệ :  \(\frac{HB}{AB}=\frac{AB}{BC}\)\(\Leftrightarrow HB=\frac{AB^2}{BC}=\frac{9}{6}=1,5\left(cm\right)\)

    Xét   \(\Delta BHD\) và  \(\Delta BAE\) có :

              \(\widehat{BHD}=\widehat{BAE}=90\)độ

              \(\widehat{ABE}=\widehat{EDH}\)( do BE là phân giác của góc B )

    \(\Leftrightarrow\Delta BHD\infty\Delta BAE\left(g.g\right)\)

Ta có tỉ lệ : \(\frac{BH}{AB}=\frac{HD}{AE}=\frac{BD}{BE}\)

    \(\Rightarrow\frac{S_{BHD}}{S_{BAE}}=\left(\frac{BH}{AB}\right)^2=\left(\frac{1,5}{3}\right)^2=\frac{1}{4}\)

BÀI NÀY MK TỪNG LÀM RÙI NÊN YÊN TÂM !!! NẾU THẤY ĐÚNG THÌ TK NKA !!!

Hàng thứ 5 từ dười đếm lên bạn sửa lại giúp mk là   \(\widehat{ABE}=\widehat{EBH}\)mới đúng !!! thông cảm mk bị cận