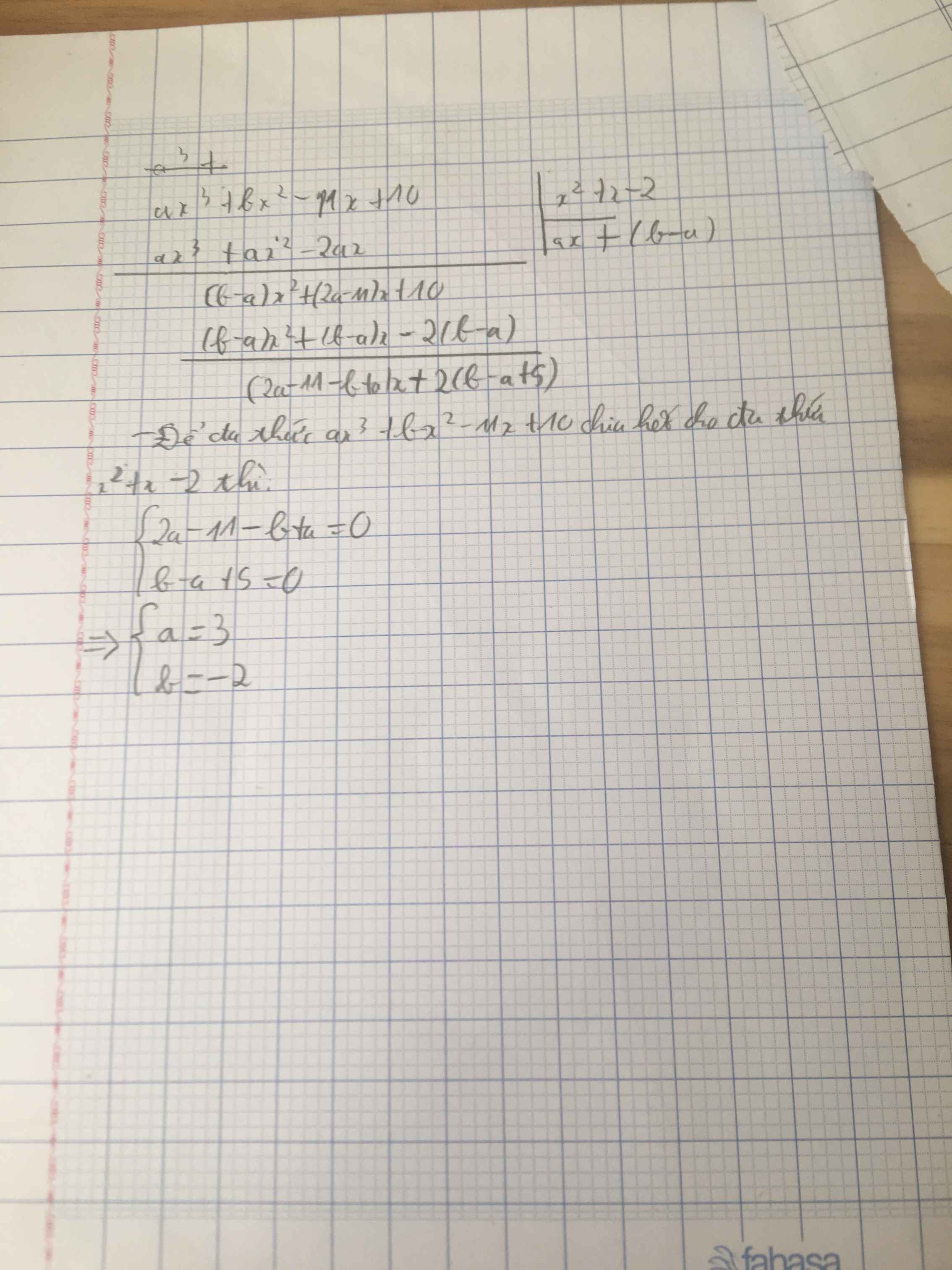Câu hỏi của Phạm Thị Quỳnh Tú - Toán lớp 8 - Học toán với OnlineMath

Tham khảo

Vì \(x^{2017}-ax^{2016}+ax-1⋮\left(x-1\right)^2\Rightarrow x^{2017}-ax^{2016}+ax-1=\left(x-1\right)^2.Q\left(x\right)\text{đúng}\forall x\)

Thay x = 1 vào đẳng thức trên, ta có: 

1 - a + a - 1 = 0 (đúng) => Có vô số số hữu tỉ a thoả mãn để bài

Lời giải:
Đặt $f(x)=ax^3+bx^2-11x+10$

$x^2+x-2=(x-1)(x+2)$

Do đó để $f(x)\vdots x^2+x-2$ thì $f(x)\vdots x-1$ và $f(x)\vdots x+2$

$\Leftrightarrow f(1)=f(-2)=0$ (theo định lý Bê-du về phép chia đa thức) 

$\Leftrightarrow a+b-1=-8a+4b+32=0$

$\Leftrightarrow a=3; b=-2$ 

Bài 1 :

x² - x - 2 = x² - 2x + x - 2

= x( x - 2 ) + ( x - 2 ) = ( x - 2 ) ( x + 1 )

Để x³ + ax + b ⋮ ( x - 2 ) ( x + 1) thì :

x³ + ax + b = ( x - 2 ) ( x + 1 ) . Q

Vì đẳng thức trên đúng với mọi x, do đó :

+) đặt x = 2 ta có :

2³ + 2a + b = ( 2 - 2 ) ( 2 + 1 ) . Q

8 + 2a + b = 0

2a + b = -8

b = -8 - 2a (1)

+) đặt x = -1 ta có :

(-1)³ + (-1)a + b = ( -1 - 2 ) ( -1 + 1 ) . Q

-1 - a + b = 0

-a + b = 1 (2)

Thay (1) vào (2) ta có :

-a - 8 - 2a = 1

<=> -3a = 9

<=> a = -3

=> b = 1 + (-3) = -2

Vậy a = -3; b = -2

Đa thức x - 1 có nghiệm \(\Leftrightarrow x-1=0\Leftrightarrow x=1\)

Vậy 1 là nghiệm của đa thức x - 1

Để đa thức x¹⁹⁹⁵ - ax¹⁹⁹⁴ + ax - 1 chia hết cho x - 1 thì 1 cũng là nghiệm của đa thức x¹⁹⁹⁵ - ax¹⁹⁹⁴ + ax - 1

Khi đó: \(1-a+a-1=0\Leftrightarrow0=0\)(đúng)

Vậy với mọi a thì đa thức x¹⁹⁹⁵ - ax¹⁹⁹⁴ + ax - 1 chia hết cho x - 1

để đa thức \(x^4-3x^3+3x^2+ax+b\) chia hết cho đa thức \(x^2-3x+4\) thì

đặt \(x^4-3x^3+3x^2+ax+b=\left(x^2-3x+4\right)\left(x^2+mx+n\right)\)

\(=x^4+\left(m-3\right)x^3+\left(n+4-3m\right)x^2+\left(4m-3n\right)x+4n\)

đồng nhất với đa thức đã cho ta được

\(\left\{{}\begin{matrix}m-3=-3\\n+4-3m=3\\4m-3n=a\\4n=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=0\\n=-1\\a=3\\b=-4\end{matrix}\right.\)

Vậy (a,b) = (3;-4)