Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi vt MA+MC=MB+MD

Những câu hỏi liên quan
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi 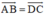
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \)
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
Đúng 1
Bình luận (0)
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow{AB}=\overrightarrow{DC}\) ?
Ta chứng minh hai mệnh đề:
- Khi =
thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
=
⇔
=
và và
cùng hướng.
và
cùng hướng =>
và
cùng phương, suy ra giá của chúng song song với nhau, hay AB // DC (1)
Ta lại có =
=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
- Khi ABCD là hình bình hành thì =
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ và
cùng hướng (3)
Mặt khác AB = CD => =
(4)
Từ (3) và (4) suy ra =
.
Đúng 1
Bình luận (0)
Cho tứ giác ABCD và một điểm M thuộc miền trong của tứ giác . Chứng minh BĐT :
a) MA + MB + MC + MD >= 1/2 *(AB+BC+CD+DA)
b) MA+MB+MC+MD >= AC+BD. Dấu "=" xảy ra khi nào?
a/ Áp dụng BĐT ba điểm :
\(AM+MB\ge AB\) ; \(BM+MC\ge BC\); \(CM+MD\ge CD\) ; \(DM+MA\ge DA\)
Cộng theo vế : \(2\left(MA+MB+MC+MD\right)\ge AB+BC+CD+DA\)
\(\Leftrightarrow MA+MB+MC+MD\ge\frac{AB+BC+CD+DA}{2}\)
Đẳng thức xảy ra khi M là giao điểm của AC và BD
b/ Ta cũng áp dụng BĐT ba điểm :
\(AM+MC\ge AC\) ; \(BM+MD\ge BD\)
Cộng theo vế : \(MA+MB+MC+MD\ge AC+BD\)
Đẳng thức xảy ra khi M là giao điểm của AC và BD
Đúng 0
Bình luận (0)
Cho 2 hình bình hành hình ABCD (tâm O) và ABEF và EH = FG = AD . Chứng minh
1.
DA - DB + DC = 0
2.
MA + MC = MB + MD (M là điểm tùy ý)
3.
OA + OB + OC + OD = AB + DA + CD + BC
4. Tứ giác CDGH là bình hành
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại M. Gọi P là trung điểm của cạnh AD. Chứng minh rằng MP vuông góc với BC khi và chỉ khi \(\overrightarrow{MA}.\overrightarrow{MC}=\overrightarrow{MB}.\overrightarrow{MD}\) ?
a) \(\overrightarrow{MP}.\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{MD}\right).\left(\overrightarrow{BM}+\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}+\overrightarrow{MD}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}-\overrightarrow{MB}.\overrightarrow{MD}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(0+0\right)=0\) (vì \(AC\perp BD\) nên \(\overrightarrow{MA}.\overrightarrow{BM}=0;\overrightarrow{MD}.\overrightarrow{MC}=0\)).
Vậy \(\overrightarrow{MP}.\overrightarrow{BC}=0\) nên \(MP\perp BC\).
Đúng 1
Bình luận (0)
1.Cho tứ giác ABCD. Chứng minh rằng \(\frac{1}{2}\)p< AC + BD< p ( với p là chu vi cùa tứ giác ABCD)
2.Cho tứ giác ABCD, M là một điểm nằm trong tứ giác đó. Xác định vị trí của M để MA+MB+MC+MD nhỏ nhất.
Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi \(\overrightarrow {BC} = \overrightarrow {AD}.\)
Tứ giác ABCD là một hình bình hành \( \Leftrightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
\( \Leftrightarrow \) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) cùng hướng và AD = BC.
\( \Leftrightarrow \overrightarrow {BC} = \overrightarrow {AD} .\) (đpcm)
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD (AB//CD)và 1 điểm M tùy ý nằm trong hình thang. Chứng minh rằng luôn dựng được 1 tứ giác nội tiếp hình thang cân ABCD mà độ dài các cạnh của tứ giác bằng độ dài các đoạn thẳng MA, MB, MC, MD .
đây là hình vẽ , mình dựng hình phụ . mình có viết được một chút đó là :
Qua M kẻ AJ//IH ; AI//JK .
nối IJ ; IK; KH ;KJ
ta có AB//CD =>IM//AJ => tứ giác AIMJ là hình thang cân
CÁC BẠN GIÚP MÌNH LÀM TIẾP VỚI Ạ!!
Đúng 0
Bình luận (0)















