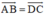Các câu hỏi tương tự
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng overrightarrow{MI}overrightarrow{IN}b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết overrightarrow{IA}+overrightarrow{IB}+overrightarrow{IC}+overrightarrow{ID}overrightarrow{0}. Chứng minh rằng tứ giác ABCD là hình bình hành
Đọc tiếp
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB = OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng \(\overrightarrow{MI}=\overrightarrow{IN}\)
b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\). Chứng minh rằng tứ giác ABCD là hình bình hành
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. Khi đó ABCD là hình bình hành nếu A.
M
N
→
A
B
→
B.
M
N
→
D
C
→
C. ...
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. Khi đó ABCD là hình bình hành nếu
A. M N → = A B →
B. M N → = D C →
C. M N → = A B → và M N → = D C →
D. D C → = A B →
Cho các mệnh đề:(1) “
3
là số vô tỉ nếu và chỉ nếu 3 là số hữu tỉ”(2) “Tứ giác là hình thang có hai cạnh bên bằng nhau nếu và chỉ nếu nó là hình bình hành”(3) “Tứ giác là hình bình hành có hai cạnh kề bằng nhau nếu và chỉ nếu nó là hình thoi”(4) “3 4 khi và chỉ khi 1 2”Số mệnh đề sai là: A. 1 B. 4 C. 2 D. 3
Đọc tiếp
Cho các mệnh đề:
(1) “ 3 là số vô tỉ nếu và chỉ nếu 3 là số hữu tỉ”
(2) “Tứ giác là hình thang có hai cạnh bên bằng nhau nếu và chỉ nếu nó là hình bình hành”
(3) “Tứ giác là hình bình hành có hai cạnh kề bằng nhau nếu và chỉ nếu nó là hình thoi”
(4) “3 > 4 khi và chỉ khi 1 > 2”
Số mệnh đề sai là:
A. 1
B. 4
C. 2
D. 3
e,Tứ giác và hình bình hành khi và chỉ khi tam giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Phát biểu mệnh đề P
⇔
Q và xét tính đúng sai của nó với:P: Tứ giác ABCD là hình thoi và Q: Tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau A. Phát biểu: Tứ giác ABCD là hình thoi nếu tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau. Mệnh đề này đúng vì mệnh đề P Q,Q P đều đúng. B. Phát biểu: Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau. Mệnh đề này đúng vì mệnh đề P Q, Q P...
Đọc tiếp
Phát biểu mệnh đề P ⇔ Q và xét tính đúng sai của nó với:
P: "Tứ giác ABCD là hình thoi" và Q:" Tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau"
A. Phát biểu: "Tứ giác ABCD là hình thoi nếu tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau". Mệnh đề này đúng vì mệnh đề P => Q,Q => P đều đúng.
B. Phát biểu: "Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau". Mệnh đề này đúng vì mệnh đề P => Q, Q => P đều đúng.
C. Phát biểu: "Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau". Mệnh đề này sai vì mệnh đề P => Q, Q => P đều sai.
D. Phát biểu: "Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau". Mệnh đề này sai vì mệnh đề P => Q sai, Q => P đúng.
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
Trong mặt phẳng Oxy, cho A(3;-1), B(2;1) và C(-2;2)a) Chứng minh rằng: A, B, C là 3 đỉnh 1 tam giácb) Tìm chu vi, diện tích của tam giác ABCc) Tìm tọa độ điểm D sao cho tứ giác ADBC là hình bình hành. Tìm tâm hình bình hànhd) Tìm tọa độ điểm E sao cho:2overrightarrow{AE}-overrightarrow{BE}2overrightarrow{EC}+overrightarrow{AC}e) Tìm tọa độ điểm M trên tia Õ sao cho: AM4f) Tìm tọa độ trọng tâm G của tam giác ABCg) Tìm tọa độ trực tâm H của tam giác ABCh) Tìm tọa độ tâm I đường tròn ngoại tiếp tam...
Đọc tiếp
Trong mặt phẳng Oxy, cho A(3;-1), B(2;1) và C(-2;2)
a) Chứng minh rằng: A, B, C là 3 đỉnh 1 tam giác
b) Tìm chu vi, diện tích của tam giác ABC
c) Tìm tọa độ điểm D sao cho tứ giác ADBC là hình bình hành. Tìm tâm hình bình hành
d) Tìm tọa độ điểm E sao cho:
\(2\overrightarrow{AE}-\overrightarrow{BE}=2\overrightarrow{EC}+\overrightarrow{AC}\)
e) Tìm tọa độ điểm M trên tia Õ sao cho: AM=4
f) Tìm tọa độ trọng tâm G của tam giác ABC
g) Tìm tọa độ trực tâm H của tam giác ABC
h) Tìm tọa độ tâm I đường tròn ngoại tiếp tam giác ABC
i) Chứng minh rằng: G, H, I thẳng hàng
j) Tìm N trên cạnh AC sao cho SABN=\(\dfrac{1}{3}S_{CBN}\)
Câu 23: Cho hai mệnh đề
P=”Tứ giác ABCD là hình thoi”, Q=”Tứ giác ABCD là hình vuông”. Khi đó mệnh đề nào sau đây đúng?
A. P => Q
B. Q => P
C. P <=> Q
D. Cả 3 đáp án trên sai
Trong các khẳng định sau, khẳng định nào đúng?a) Điểm A nằm trên trục hoành thì có hoành độ bằng 0.b) P là trung điểm của đoạn thẳng AB khi và chỉ khi hoành độ của P bằng trung bình cộng các hoành độ của A và B.c) Nếu tứ giác ABCD là hình bình hành thì trung bình cộng các tọa độ tương ứng của A và C bằng trung bình cộng các tọa độ tương ứng của B và D.
Đọc tiếp
Trong các khẳng định sau, khẳng định nào đúng?
a) Điểm A nằm trên trục hoành thì có hoành độ bằng 0.
b) P là trung điểm của đoạn thẳng AB khi và chỉ khi hoành độ của P bằng trung bình cộng các hoành độ của A và B.
c) Nếu tứ giác ABCD là hình bình hành thì trung bình cộng các tọa độ tương ứng của A và C bằng trung bình cộng các tọa độ tương ứng của B và D.