Tìm tập xác định của hàm số:
\(y=\sqrt{3tan^2x+2}\)
Hàm số y = 3 tan ( 2 x - π / 6 ) có tập xác định là:
A. ℝ \ π 6 + k π , k ∈ ℤ
B. ℝ \ π 3 + k π , k ∈ ℤ
C. ℝ \ - π 3 + k π , k ∈ ℤ
D. ℝ \ π 3 + k π 2 , k ∈ ℤ
Tìm tập xác định của hàm số sau y= 3tan 3x. cot 5x
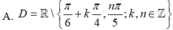
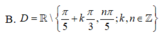
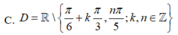
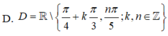
Tìm tập xác định của hàm số \(y=\dfrac{x-2}{\sqrt{2x+4}-\sqrt{4-2x}}\).
ĐKXĐ: \(\left\{{}\begin{matrix}2x+4>=0\\4-2x>=0\\\sqrt{2x+4}-\sqrt{4-2x}< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-2\\x< =2\\2x+4< >4-2x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2< =x< =2\\x< >0\end{matrix}\right.\)
Vậy: TXĐ là D=[-2;2]\{0}
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Tìm tập xác định của hàm số
y = \(\sqrt{x+8+2\sqrt{x+7}}+\dfrac{1}{1-x}\)
y= \(\sqrt{\sqrt{x^2+2x+2}-\left(x+1\right)}\)
Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt {2x - 1} + \sqrt {5 - x} \)
b) \(y = \frac{1}{{\sqrt {x - 1} }}.\)
a) Tập xác đinh của hàm số \(y = \sqrt {2x - 1} + \sqrt {5 - x} \) là:
\(\left\{ {\begin{array}{*{20}{c}}{2x - 1 \ge 0}\\{5 - x \ge 0}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{x \ge \frac{1}{2}}\\{x \le 5}\end{array}} \right.} \right.\,\, \Leftrightarrow \,\,\frac{1}{2} \le x \le 5\)
Vậy tập xác định của hàm số là: \(D = \left[ {\frac{1}{2};5} \right].\)
b) Tập xác định của hàm số \(y = \frac{1}{{\sqrt {x - 1} }}\) là: \(x - 1 > 0\,\, \Leftrightarrow \,\,x > 1.\)
Vậy tập xác định của hàm số là: \(D = \left( {1; + \infty } \right).\)
tìm tập xác định của hàm số: \(y=\sqrt{\sqrt{x^2+2x+2}-\left(x+1\right)}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x^2+2x+2\ge0\left(\text{luôn đúng}\right)\\\sqrt{x^2+2x+2}-\left(x+1\right)\ge0\left(1\right)\end{matrix}\right.\)
Xét (1), ta có:
\(\sqrt{x^2+2x+2}=\sqrt{\left(x+1\right)^2+1}>\sqrt{\left(x+1\right)^2}=\left|x+1\right|\ge x+1\)
\(\Leftrightarrow\sqrt{x^2+2x+2}-\left(x+1\right)>0\) ; \(\forall x\)
\(\Rightarrow\) BPT (1) luôn đúng với mọi x
Vậy hàm số xác định trên R
1.Tìm tập xác định của hàm số: y= \(\sqrt{1+sinx-2cos^2x}\)
2. Cho hàm số: y = \(\sqrt{sin^4x+cos^4x-2msinx.cosx}\)
Tìm các giá trị của m để xác định với mọi x.
Tìm tập xác định D của hàm số y= \(\sqrt{\sqrt{x^2+2x+2}-\left(x+1\right)}\)
Tìm tập xác định của hàm số: y=\(\frac{\sqrt{3-2x}+x\sqrt{3x+11}}{\sqrt{1-x^2}+\sqrt{\left|3x^2-2x-5\right|}}\)