bạn ơi mk gửi nhầm, mk xin lỗi nhé!

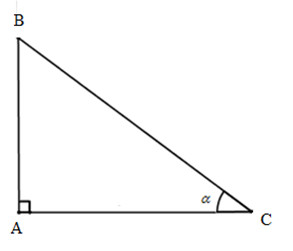
Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:

sinC>0;cosC>0;tanC>0;cotC>0sinC>0;cosC>0;tanC>0;cotC>0

Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.

Ta có:

Sin2C+cos2C=1Sin2C+cos2C=1

⇒cos2C=1−sin2C=1−(0,8)2=0,36⇒cos2C=1−sin2C=1−(0,8)2=0,36

⇒cosC=0,6;⇒cosC=0,6;

tgC=sinCcosC=0,80,6=43;tgC=sinCcosC=0,80,6=43;

cotgC=cosCsinC=0,60,8=34

Vì hai góc B và C phụ nhau nên sinC=cosB=0,8.

Ta có:

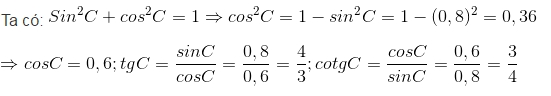
Nhận xét: Nếu biết sinα (hay cosα) thì ta có thể tính được ba tỷ số lượng giác còn lại.

Hướng dẫn giải:

Vì hai góc B và C phụ nhau nên sinC=cosB=0,8.

Ta có: Sin2C+cos2C=1⇒cos2C=1−sin2C=1−(0,8)2=0,36

⇒cosC=0,6;tgC=sinCcosC=0,80,6=43;cotgC=cosCsinC=0,60,8=34

Nhận xét: Nếu biết sinα (hay cosα) thì ta có thể tính được ba tỷ số lượng giác còn lại.

Có : ΔABC vuông tại A => sinB = cosC = \(\frac{3}{4}\)

Mà lại có : sin² B + cos²B = 1

=> cos²B = 1 - sin²B

=> cosB = 1 - \(\frac{3}{4}\)= \(\frac{1}{4}\)

1+tan^2B=1/cos^2B=1:0,64=1:16/25=25/16

=>tan^2B+9/16

=>tan B=3/4

Bài 1:

              \(BC=CD+BD=68+51=119\)

\(AD\)là phân giác  \(\widehat{BAC}\)\(\Rightarrow\)\(\frac{BD}{AB}=\frac{DC}{AC}\)hay     \(\frac{51}{AB}=\frac{68}{AC}\)

\(\Leftrightarrow\)\(\frac{51^2}{AB^2}=\frac{68^2}{AC^2}=\frac{51^2+68^2}{AB^2+AC^2}=\frac{25}{49}\)

suy ra:    \(\frac{51^2}{AB^2}=\frac{25}{49}\)\(\Rightarrow\)\(AB=71,4\)

ÁP dụng hệ thức lượng ta có:

           \(AB^2=BH.BC\)

\(\Leftrightarrow\)\(BH=\frac{AB^2}{BC}=\frac{71,4^2}{119}=42,84\)

\(\Rightarrow\)\(CH=BC-BH=119-42,84=76,16\)

Bài 2:

Áp dụng Pytago ta có:

     \(AH^2+BH^2=AB^2\)

\(\Leftrightarrow\)\(BH^2=AB^2-AH^2\)

\(\Leftrightarrow\)\(BH^2=7,5^2-6^2=20,25\)

\(\Leftrightarrow\)\(BH=4,5\)

Áp dụng hệ thức lượng ta có:

       \(AB^2=BH.BC\)

\(\Rightarrow\)\(BC=\frac{AB^2}{BH}=\frac{7,5^2}{4,5}=12,5\)

       \(AB.AC=BC.AH\)

\(\Rightarrow\)\(AC=\frac{BC.AH}{AB}=\frac{12,5.6}{7,5}=10\)

b)   \(cosB=\frac{AC}{BC}=\frac{10}{12,5}=0.8\)

      \(cosC=\frac{AB}{BC}=\frac{7,5}{12,5}=0,6\)

\(AB^2=AH.BC\Rightarrow BC=\frac{AB^2}{AH}=\frac{7,5^2}{6}=9,375\)

áp dụng định lí Pytago tính được AC = 5,625

tính cosB và cos C thì quá dễ rồi. bạn làm tiếp nhé