Tìm phương trình chính tắc của elip đi qua hai điểm (2;1) và có tiêu cự là 2√3

Những câu hỏi liên quan
viết phương trình chính tắc của elip các trường hợp sau 1. elip đi qua điểm M(0;3) và có tiêu điểm F2(5;0) 2. Elip đi qua hai điểm A(7;0), B(0;3) 3. Elip đi qua hai điểm A(0;1), N(1; căn 3 / 2)
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1
Đúng 2
Bình luận (0)
Tìm phương trình chính tắc của Elip đi qua điểm (6; 0) và có tâm sai bằng 1/2 A. B. C. D.
Đọc tiếp
Tìm phương trình chính tắc của Elip đi qua điểm (6; 0) và có tâm sai bằng 1/2
A. 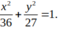
B. 
C. ![]()
D. ![]()
Do tâm sai của ( E) là 1/2 nên
![]()
mà Elip qua điểm (6;0) nên a= 6
=> c= 3 => b2= a2- c2= 36- 9= 27
Vậy
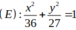
Chọn A.
Đúng 0
Bình luận (0)
Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và đi qua điểm (2;-2).
Đọc tiếp
Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và đi qua điểm (2;-2).
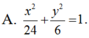
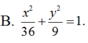
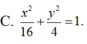
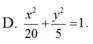
Đáp án D
Gọi phương trình chính tắc của Elip có dạng:
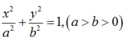
Theo đề bài: Trục lớn gấp đôi trục bé nên a= 2b => a2= 4b2
Điểm (2; -2) thuộc Elip:
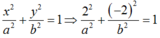
Ta được hệ:
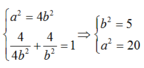
Vậy phương trình (E) cần tìm là :
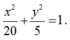
Đúng 0
Bình luận (0)
Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm M(2; -2). A.
x
2
20
+
y
2
5
1.
B.
x
2
36
+
y
2
9
1.
C. ...
Đọc tiếp
Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm M(2; -2).
A. x 2 20 + y 2 5 = 1.
B. x 2 36 + y 2 9 = 1.
C. x 2 24 + y 2 6 = 1.
D. x 2 16 + y 2 4 = 1.
Lập phương trình chính tắc của elip đi qua hai điểm \(A\left( {5;0} \right)\) và có một tiêu điểm là \({F_2}\left( {3;0} \right)\).
Phương trình chính tắc của elip có dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\).
Elip đi qua \(A\left( {5;0} \right)\) nên ta có \(\frac{{{5^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Leftrightarrow {a^2} = 25\)
Mặt khác elip có một tiêu điểm \({F_2} = \left( {3;0} \right)\) nên ta có \(c = 3\), suy ra \({b^2} = {a^2} - {c^2} = 25 - {3^2} = 16\)
Vậy phương trình của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
Đúng 0
Bình luận (0)
Phương trình chính tắc của elip đi qua điểm (5;0) và có tiêu cự bằng 2 căn 5
\(F_1F_2=2c=2\sqrt{5}\)
\(\Rightarrow c=\dfrac{2\sqrt{5}}{2}=\sqrt{5}\)
\(\left(E\right)\) qua \(\left(5;0\right)\Rightarrow a=5\)
Ta có : \(b=\sqrt{a^2-c^2}\)
\(\Rightarrow b^2=a^2-c^2\)
\(\Rightarrow b^2=5^2-\sqrt{5}^2\)
\(\Rightarrow b^2=25-5=20\)
Vậy \(PTCT\left(E\right):\dfrac{x^2}{25}+\dfrac{y^2}{20}=1\)
Đúng 3
Bình luận (1)
Tìm phương trình chính tắc của elip nếu nó đi qua điểm
A
2
;
3
và tỉ số của độ dài trục lớn với tiêu cự bằng
2
3
A.
x
2
16
+
y
2
4
1.
B.
x
2...
Đọc tiếp
Tìm phương trình chính tắc của elip nếu nó đi qua điểm A 2 ; 3 và tỉ số của độ dài trục lớn với tiêu cự bằng 2 3
A. x 2 16 + y 2 4 = 1.
B. x 2 4 + y 2 3 = 1.
C. x 2 8 + y 2 6 = 1.
D. x 2 4 + y 2 16 = 1.
Gọi phương trình chính tắc của elip là: x 2 a 2 + y 2 b 2 = 1
Vì elip đi qua điểm A 2 ; 3 do đó thay tọa độ điểm A vào ta được
4 a 2 + 3 b 2 = 1 (1)
Theo đề bài tỉ số của độ dài trục lớn và tiêu cực là
2 a 2 c = a c = 2 3 ⇔ a = 2 c 3 ⇔ 3 a 2 = 4 c 2
Mà c 2 = a 2 - b 2 ta có 3 a 2 = 4 a 2 - b 2 ⇔ a 2 - 4 b 2 = 0 (2)

Đúng 0
Bình luận (0)
Tìm phương trình chính tắc của elip nếu nó đi qua điểm
A
2
;
3
và tỉ số của độ dài trục lớn với tiêu cự bằng
2
3
A.
x
2
16
+
y
2
4
1.
B.
x
2...
Đọc tiếp
Tìm phương trình chính tắc của elip nếu nó đi qua điểm A 2 ; 3 và tỉ số của độ dài trục lớn với tiêu cự bằng 2 3
A. x 2 16 + y 2 4 = 1.
B. x 2 4 + y 2 3 = 1.
C. x 2 3 + y 2 4 = 1.
D. x 2 4 + y 2 16 = 1.
Lập phương trình chính tắc của elip trong trường hợp sau: Elip đi qua các điểm M(0; 3) và N(3; -12/5)
Gọi Elip cần tìm có dạng : (E) : 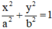
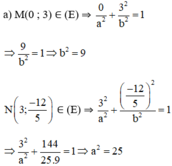
Vậy phương trình chính tắc của elip: 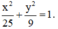
Đúng 0
Bình luận (0)
Phương trình chính tắc của elip có một tiêu điểm
F
1
2
;
0
và đi qua điểm
M
2
;
1
là
Đọc tiếp
Phương trình chính tắc của elip có một tiêu điểm F 1 2 ; 0 và đi qua điểm M 2 ; 1 là
![]()
![]()
![]()
![]()















