diện tích tam giác ABC là:4x5:2=10(cm²)

đúng rồi mà

lí do bạn sai là vì đây k phải là cách tính diện tích tam giác vuông 

tam giác cân có 2 cạnh bằng nhau cân ở a nên ta có hình 

Diện tích tam giác ABC là :

( 4 x 5 ) : 2 = 10 ( cm² )

                Đáp số : 10 cm²

Tam giác vuông HAB có:

   \(HB^2=AB^2-AH^2=5^2-4^2=9\)

=> \(HB=3\) => \(BC=2.HB=2.3=6\)

Diện tích tam giác ABC là \(\frac{1}{2}BC.AH=\frac{1}{2}.6.4=12\left(cm^2\right)\)

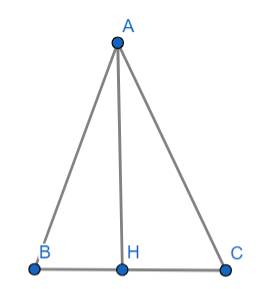
Xét tam giác vuông ABH vuông tại H ta có: 

\(AB^2=BH^2+AH^2\)

\(\Rightarrow AH=\sqrt{AB^2-BH^2}\)

\(\Rightarrow AH=\sqrt{6^2-5^2}=\sqrt{11}\left(cm\right)\)

Mà tam giác ABC cân tại A nên \(BC=2BH=2\cdot5=10\left(cm\right)\)  

Diện tích tam giác ABC là: 

\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot\sqrt{11}=5\sqrt{11}\left(cm^2\right)\)

Diện tích tam giác abc là :

       5 x 6 : 2 = 15 ( cm² )

                Đáp số : 15 cm²

Diện tích hình tam giác ABC là : 

                   5 x 6 : 2 = 15 (cm2)

                       Đáp số : 15 cm2

Diện tích hình tam giác abc là 

      6*5:2=15 (cm)

                  DS: 15 cm

giúp mik ik mn

a) Xét ΔABD và ΔACD có 

AB=AC(ΔABC cân tại A)

\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))

AD chung

Do đó: ΔABD=ΔACD(c-g-c)

Suy ra: BD=CD(hai cạnh tương ứng)

mà B,D,C thẳng hàng(gt)

nên D là trung điểm của BC

Xét ΔABC có 

AD là đường trung tuyến ứng với cạnh BC(cmt)

BE là đường trung tuyến ứng với cạnh BC(gt)

AD cắt BE tại O(gt)

Do đó: O là trọng tâm của ΔABC(Định lí ba đường trung tuyến của tam giác)

b) Ta có: D là trung điểm của BC(cmt)

nên \(BD=CD=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)

Ta có: ΔABD=ΔACD(cmt)

nên \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)

mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)

nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)

Áp dụng định lí Pytago vào ΔABD vuông tại D, ta được:

\(AB^2=AD^2+BD^2\)

\(\Leftrightarrow AD^2=5^2-4^2=25-16=9\)

hay AD=3(cm)

Xét ΔABC có 

AD là đường trung tuyến ứng với cạnh CB(cmt)

O là trọng tâm của ΔABC(cmt)

Do đó: \(OD=\dfrac{1}{3}AD\)(Tính chất trọng tâm của tam giác)

hay OD=1(cm)

Vậy: OD=1cm

c) Xét ΔABC có 

O là giao điểm của 3 đường phân giác

O là giao điểm của 3 đường trung tuyến

Do đó: ΔABC đều

H là điểm nào hả bạn?

/\ABC vuông cân tại A =>AB = AC = 5 cm

Ap dụng định lý pytago vào tam giác vuông ABC => AB^2 + AC^2       =  BC^2

                                                                              = 5^2 + 5^2             = 50

                                                                              => BC = √50 cm

a: ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC và AH là phân giác của góc BAC

=>HB=HC

b: HB=HC=3cm

=>AH=4cm

AH là phân giác của góc BAC

=>góc BAH=góc CAH

c: Xét ΔAMH vuông tại M và ΔANH vuông tại N có

AH chung

góc MAH=góc NAH

=>ΔAMH=ΔANH

=>HM=HN

=>ΔHMN cân tại H

a: AB<AC<BC

=>góc C<góc B<góc A

b: Xét ΔCBM có

CA vừa là đường cao, vừa là trung tuyến

=>ΔCBM cân tại C

c: N ở đâu vậy bạn?