1. Biểu thức am+3: am+2 bằng bao nhiu

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng: A.
2
B.
6
C. 6 D. 2
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 = 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng:
A. 2
B. 6
C. 6
D. 2
Chọn A
Gọi G là trọng tâm tam giác ABC. Ta có G (0; 0; 3) và G ∉ (S)
Khi đó:
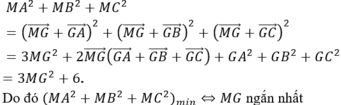
Ta lại có, mặt cầu (S) có bán kính R = 1 tâm I (0;0;1) thuộc trục Oz, và (S) qua O.
Mà G ∈ Oz nên MG ngắn nhất khi M = Oz ∩ (S). Do đó M (0;0;2). Vậy MA = √2
Đúng 0
Bình luận (0)
tính giá trị biểu thức sau bằng cách hợp lí
A=\(x^5\)-70\(x^4\)-70\(x^3\)-70\(x^2\)-70x+34 tại x=71
(gợi ý:thay 70 trong biểu thức bởi x-1)
giúp với muốn tick bao nhiu cung đc miễn phí ok
chị mua sách giải về tham khảo nha!
chúc chị hok tốt!
Đúng 0
Bình luận (0)
\(A=x^5-70x^4-70x^3-70x^2-70x+34\)
\(\Rightarrow A=x^5-\left(x-1\right)x^4-\left(x-1\right)x^3-\left(x-1\right)x^2-\left(x-1\right)x+34\)
\(A=x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2+x+34\)
\(A=71+34\)
\(A=105\)
Đúng 0
Bình luận (0)
Cho mạch điện xoay chiều hai đầu AB, gồm hai đoạn AM và MB mắc nối tiếp nhau. Điện áp tức thời giữa hai đầu AB, AM, MB tương ứng là uAB,
u
A
M
,
u
M
B
, được biểu diễn bằng đồ thị hình bên theo thời gian t. Biết cường độ dòng điện trong mạch có biểu thức i
2
cos(ωt) A. Công suất tiêu thụ trên các đoạn mạch AM và MB lần...
Đọc tiếp
Cho mạch điện xoay chiều hai đầu AB, gồm hai đoạn AM và MB mắc nối tiếp nhau. Điện áp tức thời giữa hai đầu AB, AM, MB tương ứng là uAB, u A M , u M B , được biểu diễn bằng đồ thị hình bên theo thời gian t. Biết cường độ dòng điện trong mạch có biểu thức i = 2 cos(ωt) A. Công suất tiêu thụ trên các đoạn mạch AM và MB lần lượt là
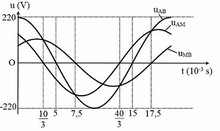
A. 98,62 W và 56,94 W
B. 139,47 W và 80,52 W
C. 82,06 W và 40,25 W
D. 90,18 W và 53,33 W
Cho hình vuông ABCD cạnh 1, gọi M là một điểm nằm giữa B và C. Tia AM cắt đường thẳng CD tại N. Tính giá trị biểu thức P=1/AM2 + 1/AN2\(\frac{1}{AM^2}+\frac{1}{AN^2}\)
Trong tam giác ABC có đường trung tuyến AM , K là 1 điểm nằm trên AM sao cho AK/ AM bằng 1/2. BK cắt AC ở N. Biết diện tích tam giác ABC bằng 60. Khi đó diện tích tam giác AKN bằng bao nhiêu
*MO//BN (O thuộc AC).
\(\dfrac{AK}{AM}=\dfrac{1}{2}\Rightarrow\)K là trung điểm AM.
-△AMO có: K là trung điểm AM, KN//MO \(\Rightarrow\)N là trung điểm AO.
-△BNC có: MO//BN, M là trung điểm BC \(\Rightarrow\)O là trung điểm NC.
\(\Rightarrow AN=ON=OC=\dfrac{1}{3}AC\)
\(\dfrac{S_{AKN}}{S_{ABC}}=\dfrac{S_{AKN}}{S_{AMC}}.\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{AN}{AC}.\dfrac{MC}{BC}=\dfrac{1}{3}.\dfrac{1}{2}=\dfrac{1}{6}\)
\(\Rightarrow S_{AKN}=\dfrac{S_{ABC}}{6}=\dfrac{60}{6}=10\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Giúp mình với mình cần gấp: cho mnp khác 0, am+bn+cp khác 0 thỏa mãn m=bn+cp,n=am+cp,p=am+bn tính giá trị biểu thức A=1/1+a + 1/1+b +1/1+c
Ta có: \(m+n+p=2ma+2np+2pc\Rightarrow ma+np+pc=\frac{1}{2}\left(m+n+p\right)\)(1)
lại có:
\(\hept{\begin{cases}m=bn+cp\\n=am+cp\\p=am+bn\end{cases}\Rightarrow}\hept{\begin{cases}m-n=bn-am\\n-p=cp-bn\\p-m=am-cp\end{cases}}\Rightarrow\hept{\begin{cases}m\left(a+1\right)=n\left(b+1\right)\\n\left(b+1\right)=p\left(c+1\right)\\p\left(c+1\right)=m\left(a+1\right)\end{cases}}\)
\(\Rightarrow\frac{1}{m\left(a+1\right)}=\frac{1}{n\left(b+1\right)}=\frac{1}{p\left(c+1\right)}=\frac{3}{ma+mb+mc+m+n+p}\)( Dãy tỉ số bằng nhau)
\(=\frac{3}{\frac{1}{2}\left(m+n+p\right)+n+m+p}=\frac{2}{n+m+p}\)
=> \(\frac{1}{a+1}=\frac{2m}{m+n+p}\)
\(\frac{1}{b+1}=\frac{2n}{m+n+p}\)
\(\frac{1}{c+1}=\frac{2p}{m+n+p}\)
=> \(A=\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}=\frac{2m+2n+2p}{m+n+p}=2\)
Tìm tất cả các cách thay thế các dấu ? bới các phép tính = , -, *, / trong biểu thức dưới đây sao cho biểu thức có ía trị bằng 35 :
(((( 1 ? 2 ) ? 3 ) ? 4) ? 5) ? 6
đang càn gấp mong anh chị nào nhìn thấy thì giúp hộ nhanh nha ...thw nhiu lám ... <3 <3 <3
Cho hình vuông ABCD cạnh a. Gọi M là một điểm nằm giữa B và C. Tia AM cắt đường thẳng CD tại N. Chứng minh giá trị biểu thức P=\(\dfrac{1}{AM^2}+\dfrac{1}{AN^2}\) luôn không đổi khi M di chuyển trên B và C
cho tam giác ABC có đường trung tuyến AM và G là trọng tâm của tam giác ABC trong các hệ thức sau hệ thức nào sai
1.AG=1/3 AM
2.AG=2/3AM
3.GM=1/3AM
4.AM=3/2AG
Xem thêm câu trả lời



























