Thu gọn đa thức sau:
M = x^3 + y^3 + z^3 + x^3 - y^3 + z^3 + x^3 + y^3 - z^3
Những câu hỏi liên quan
thu gọn đa thức sau
M= x^3+y^3+z^3+x^3-y^3+z^3+x^3+y^3-z^3
\(M=x^3+y^3+z^3+x^3-y^3+z^3+x^3+y^3-z^3.\)
\(=\left(x^3+x^3+x^3\right)+\left(y^3-y^3+y^3\right)+\left(z^3+z^3-z^3\right)\)
\(=3x^3+y^3+z^3\)
Đúng 0
Bình luận (0)
Ta có:
M=x3+y3+z3+x3-y3+z3+x3+y3-z3
=(x3+x3+x3)+(y3-y3+y3)+(z3+z3-z3)
=3x3+y3+z3
Vậy M=3x3+y3+z3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
2. Thu gọn đa thức sau:
M= \(x^3+y^3+z^3+x^3-y^3+z^3+x^3+y^3-z^3\)
M = ( x\(^3\) + x\(^3\) + x\(^3\) ) + ( y\(^3\) - y\(^3\) + y\(^3\) ) + ( z\(^3\) + z3 - z\(^3\) )
= 3x\(^3\) + y\(^3\) + z\(^3\)
Đúng 0
Bình luận (0)
1.tìm bậc của mỗi đa thức sau:
a)4x3 - 2/3x + 5 - 2x + x3
b)5x2 + 11x3 - 3x3 + 8x3 - 3x2
2. thu gọn đa thức sau :
M= x3 + y3 + z3 + x3 - y3 + z3 + x3 + y3 - z3
Bài 1: Bậc của đa thức là gì?
Bài 2:
Ta có: \(M=x^3+y^3+z^3+x^3-y^3+z^3+x^3+y^3-z^3\)
\(\Rightarrow M=\left(x^3+x^3+x^3\right)+\left(y^3-y^3+y^3\right)+\left(z^3+z^3-z^3\right)\)
\(\Rightarrow M=3x^3+y^3+z^3\)
Đúng 0
Bình luận (4)
Bài 1 :
a) 4x3 - \(\dfrac{2}{3}x\) + 5 - 2x + x3
= ( 4x3 + x3 ) - ( \(\dfrac{2}{3}x\) + 2x ) + 5
= 5x3 - \(\dfrac{8}{3}x\) + 5
\(\rightarrow\) Bậc của đa thức là 3
b) 5x2 + 11x3 - 3x3 + 8x3 - 3x2
= ( 5x2 - 3x2 ) + ( 11x3 - 3x3 + 8x3 )
= 2x2 + 16x3
\(\rightarrow\) Bậc của đa thức là 3
Bài 2 :
M = x3 + y3 + z3 + x3 - y3 + z3 + x3 + y3 - z3
M = ( x3 + x3 + x3 ) + ( y3 - y3 + y3 ) + ( z3 + z3 - z3 )
M = 3x3 + y3 + z3
Đúng 0
Bình luận (0)
1a) bậc của đa thức là 8
b)bậc của đa thức là 13
2) 3x^3+y^3+z^3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
SGK Cánh Diều trang 6
19 tháng 7 2023 lúc 12:49
Thu gọn mỗi đơn thức sau: \({y^3}{y^2}z\);\(\dfrac{1}{3}x{y^2}{x^3}z\)
\({y^3}{y^2}z = {y^5}z\)
\(\dfrac{1}{3}x{y^2}{x^3}z = \dfrac{1}{3}{x^4}{y^2}z\)
Đúng 0
Bình luận (0)
Rút gọn các phân thức sau: a) x^3+y^3+z^3-3xyz/(x-y)^2+(x-z)^2+(y-z)^2 b) (x^2-y^2)^3+(y^2-z^2)^3+(z^2-x^2)^3/(x-y)^3+(y-z)^3+(z-x)3
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.
Đúng 0
Bình luận (0)
20 tháng 5 2022 lúc 10:56
Bài 2: Cho đa thức A -4x^5y^3+ 6x^4y^3- 3x^2y^3z^2+ 4x^5y^3- x^4y^3+ 3x^2y^3z^2- 2y^4+22a) Thu gọn rồi tìm bậc của đa thức Ab) Tìm đa thức B, biết rằng: B-5y^4A
Đọc tiếp
Bài 2: Cho đa thức A= -4\(x^5\)\(y^3\)+ 6\(x^4\)\(y^3\)- 3\(x^2\)\(y^3\)\(z^2\)+ 4\(x^5\)\(y^3\)- \(x^4y^3\)+ 3\(x^2y^3z^2\)- 2\(y^4\)+22
a) Thu gọn rồi tìm bậc của đa thức A
b) Tìm đa thức B, biết rằng: B-\(5y^4\)=A
`a)`
`A=-4x^5y^3+6x^4y^3-3x^2y^3z^2+4x^5y^3-x^4y^3+3x^2y^3z^2-2y^4+22`
`A=(-4x^5y^3+4x^5y^3)+(6x^4y^3-x^4y^3)-(3x^2y^3z^2-3x^2y^3z^2)-2y^4+22`
`A=5x^4y^3-2y^4+22`
`->` Bậc: `7`
`b)B-5y^4=A`
`=>B=A+5y^4`
`=>B=5x^4y^3-2y^4+22+5y^4`
`=>B=5x^4y^3+3y^4+22`
Đúng 3
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
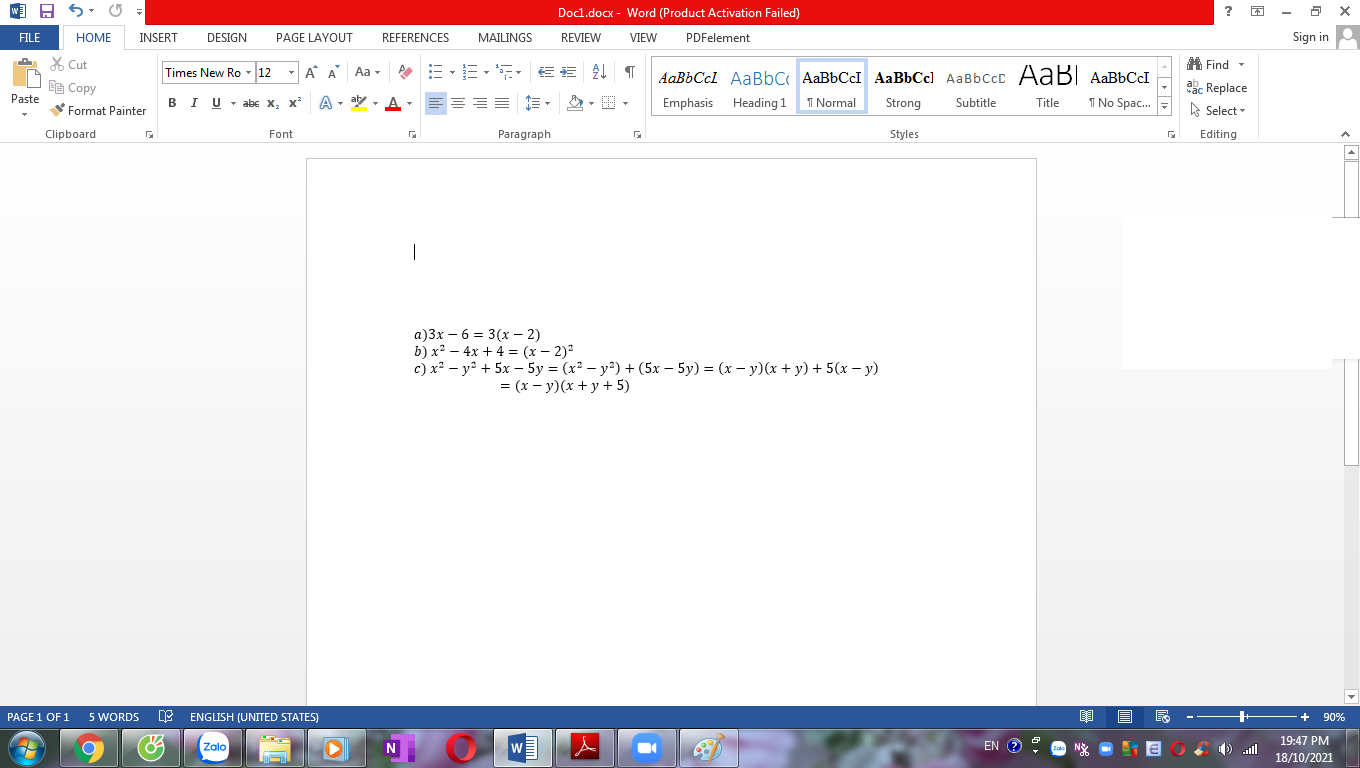
a) 3x-6
b) x2-4x+4
c) x2-y2+5x-5y
d) 8(x+y+z)3-(x+y)3-(y+z)3-(y+z)3-(z+x)3
Do câu d mình ko biết làm bởi v mình không làm được
Đúng 0
Bình luận (0)
25 tháng 9 2021 lúc 16:17
1)Rút gọn bt
a)3x2(x+1)(x-1)-(x2-1)(x4+x2+1)+(x2-1)3
b)(x+y+z)3+(x-y-z)3+(y-x-z)3+(z-y-x)3
2)Phân tích đa thức thành nhân tử:
(x-1)(x+2)(x+3)(x+6)-6(x2+5x)2+45
1)
a) \(=3x^2\left(x^2-1\right)-\left(x^3-1\right)+x^8-3x^4+3x^2-1\)
\(=3x^4-3x^2-x^3+1+x^8-3x^4+3x^2-1=x^8-x^3\)
2)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)-6\left(x^2+5x\right)+45\)
\(=\left(x^2+5x\right)^2-6\left(x^2+5x\right)-36+45\)
\(=\left(x^2+5x\right)^2-6\left(x^2+5x\right)+9=\left(x^2+5x-3\right)^2\)
Đúng 0
Bình luận (0)
Phân tích đa thức sau thành nhân tử
8(x+y+z)^3 - (x+y)^3 - (y+z)^3 - (z-x)^3
-(z+x)3 mới đúng-
đặt x+y=a , y+z=b , z+x=c thì a+b+c=2(x+y+z)
ta có 8(x+y+z)3-(x+y)3-(y+z)3-(z+x)3=[2(x+y+z)]3-(x+y)3-(y+z)3-(z+x)3=(a+b+c)3-a3-b3-c3=3(a+b)(b+c)(c+a)
=3(x+2y+z)(y+2z+x)(z+2x+y)
Đúng 0
Bình luận (0)