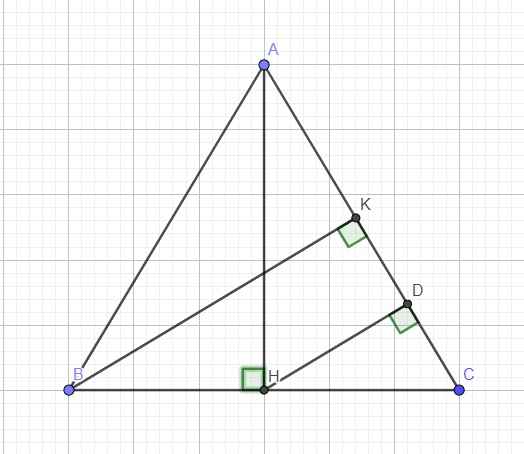
Cho tam giác ABC cân tại A có AH và BK là các đường cao. Chứng minh: 1/BK2= 1/BC2+ 1/4AH2

Những câu hỏi liên quan
Cho tam giác ABC cân tại A có các đường cao AH và BK. Chứng minh rằng : \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)
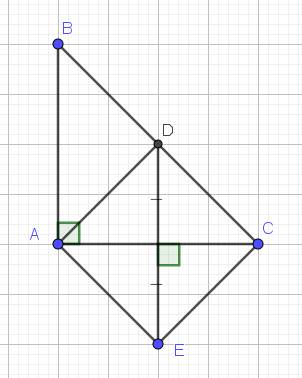
Lấy E sao cho A là trung điểm của CE
Xét ΔEBC có
BA là đường trung tuyến
BA=CE/2
Do đó: ΔEBC vuông tại E
Xét ΔCBE có AH//BE
nên AH/BE=CH/CB=1/2
=>AH=1/2BE
Xét ΔBEC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BE^2}\)
=>\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, đường cao AH và BK. Chứng minh
\(\frac{1}{BK^2}=\frac{1}{BC^2}+\frac{1}{4AH^2}\)
Từ H kẻ \(HD\perp AC\Rightarrow HD||BK\) (cùng vuông góc AC)
Mà ABC cân tại A \(\Rightarrow\) H là trung điểm BC \(\Rightarrow HC=\dfrac{BC}{2}\)
\(\Rightarrow\) HD là đường trung bình tam giác BCK
\(\Rightarrow HD=\dfrac{BK}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao HD ứng với cạnh huyền:
\(\dfrac{1}{HD^2}=\dfrac{1}{AH^2}+\dfrac{1}{CH^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{BK}{2}\right)^2}=\dfrac{1}{AH^2}+\dfrac{1}{\left(\dfrac{BC}{2}\right)^2}\)
\(\Leftrightarrow\dfrac{4}{BK^2}=\dfrac{1}{AH^2}+\dfrac{4}{BC^2}\)
\(\Leftrightarrow\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)
Đúng 2
Bình luận (2)
cho tam giác ABC cân tại A , đường cao AH , BK
Chứng minh : 1/BK^2=1/BC^2+1/AH^2
kẻ 1 đường thẳng vuông góc với BC cắt AC ở E
Xét tam giác CBE vuông tại B có:
1/BK^2=1/BC^2+1/BE^2 (hệ thức lượng)(1)
ta lại có:
*AH vuông góc với BC
BE vuông góc với BC
=>AH//BE (2)
*tam giác ABC cân tại A có:
AH là đường cao của tam gic1 ABC nên:
AH cũng là đường trung tuyến của tam giác ABC
=>H là trung điểm của BC (3)
từ (2) và (3) suy ra:
A là trung điểm của CE (4)
từ (3) và (4) suy ra:
AH là đường trung bình của tam giác CBE
=> AH=BE/2
=>BE=2AH
=>BE2=4AH2 (5)
từ (1) và (5) suy ra:
1/BK^2=1/BC^2+1/4AH^2
Đúng 0
Bình luận (0)
Bài 1: Cho hình thang cân ABCD ( AB//CD) có D^=700
a) Tính số đo các góc B^,C^,A^
b) Kẻ đường cao AH và BK của hình thang. Chứng minh DH = CK
Bài 2: Cho tam giác ABC cân tại A. kẻ phân giác BE, CF của các góc B và C.
a) Chứng minh tam giác AEF cân
b) Chứng minh △BFC = △CEB
c) Chứng minh BFEC là hình thang cân
Cho tam giác ABC cân tại A, đường cao AH và trung tuyến BK cắt nhau tại G. Tia CG cắt AB tại I
Cho tam giác ABC cân tại A; đường cao AH và trung tuyến BK cắt nhau tại G. Tia CG cắt AB tại I
a, Chứng minh tam giác AIG = tam giác AKG
b, Biết AH = 18 cm, BC = 16cm. Tính độ dài đoạn thẳng GI
c, Chứng minh IK // BC
Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
Đúng 2
Bình luận (0)
refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
Đúng 3
Bình luận (0)
1. Cho tam giác ABC có diện tích bằng 24cm2, đường cao AH bằng 6 cm. Tính BC
2. Cho tam giác ABC vuông cân tại A (AD là phân giác CD thuộc BC), E là điểm đối xứng với D qua AC. Tứ giác AECD là hình gì?
3. Cho tam giác nhọn ABC, các đường cao BH và CK. Gọi E và F lần lượt là hình chiếu của B và C trên HK. Chứng minh rằng EK = HF
Bài 2:
Tam giác $ABC$ cân tại $A$ nên phân giác $AD$ đồng thời là đường cao
$\Rightarrow AD\perp DC$. Mà $\widehat{DAC}=\widehat{BAC}:2 =45^0$ nên $\triangle DAC$ vuông cân tại $D$
$\Rightarrow DA=DC(1)$
$D,E$ đối xứng với nhau qua $AC$ nên $AC$ là trung trực của $DE$
$\Rightarrow CD=CE; AD=AE(2)$
Từ $(1); (2)\Rightarrow AD=DC=CE=EA$
$\Rightarrow ADCE$ là hình thoi.
Mà $\widehat{ADC}=90^0$ nên $ADCE$ là hình vuông.
Đúng 1
Bình luận (0)
Bài 3:
Xét tam giác $ABH$ và $ACK$ có:
$\widehat{AHB}=\widehat{AKC}=90^0$
$\widehat{A}$ chung
$\Rightarrow \triangle ABH\sim \triangle ACK$ (g.g)
$\Rightarrow \frac{AB}{AH}=\frac{AC}{AK}$
Xét tam giác $AKH$ và $ACB$ có:
$\widehat{A}$ chung
$\frac{AH}{AB}=\frac{AK}{AC}$ (cmt)
$\Rightarrow \triangle AKH\sim \triangle ACB$ (c.g.c)
$\Rightarrow \widehat{K_2}=\widehat{ACB}$ và $\widehat{H_1}=\widehat{ABC}$
Xét tam giác $KEB$ và $CHB$ có:
$\widehat{KEB}=\widehat{CHB}=90^0$
$\widehat{K_1}=\widehat{K_2}=\widehat{ACB}=\widehat{HCB}$ (cmt)
$\Rightarrow \triangle KEB\sim \triangle CHB$ (g.g)
$\Rightarrow \frac{KE}{KB}=\frac{CH}{CB}(1)$
Tương tự:
$\triangle CFH\sim \triangle CKB$ (c.g.c)
$\Rightarrow \frac{CH}{FH}=\frac{CB}{KB}(2)$
Từ $(1); (2)\Rightarrow \frac{KE}{KB}.\frac{CH}{FH}=\frac{CH}{CB}.\frac{CB}{KB}$
$\Rightarrow \frac{KE}{HF}=1$
$\Rightarrow KE=HF$ (đpcm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A, đường cao AH và BK. Chứng minh
\(\frac{1}{BK^2}=\frac{1}{BC^2}+\frac{1}{4AH^2}\)
Lấy E sao cho A là trung điểm của CE
Xét ΔEBC có
BA là đường trung tuyến
BA=CE/2
Do đó: ΔEBC vuông tại E
Xét ΔCBE có AH//BE
nên AH/BE=CH/CB=1/2
=>AH=1/2BE
Xét ΔBEC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BE^2}\)
=>\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường cao BK và CI cắt nhau tại H.
a. Chứng minh BI.BA+CK.CA= BC2
Gọi giao của AH với BC là E
=>AH vuông góc BC tại E
Xét ΔBIC vuông tại I và ΔBEA vuông tại E có
góc EBA chung
=>ΔBIC đồng dạng với ΔBEA
=>BI/BE=BC/BA
=>BE*BC=BA*BI
Xét ΔCKB vuông tại K và ΔCEA vuông tại E có
góc KCB chung
=>ΔCKB đồng dạng với ΔCEA
=>CK/CE=CB/CA
=>CK*CA=CE*CB
BI*BA+CK*CA
=BE*BC+CE*BC
=BC^2
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có các đường cao AH và BK cắt nhau tại I. Chứng minh:
a, Đường tròn đường kính AI đi qua K
b, HK là tiếp tuyến của đường tròn đường kính AI
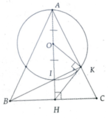
a, Chứng minh được B K A ^ = 90 0
b, Gọi O là trung điểm AI
Ta có:
+ OK = OA => O K A ^ = O A K ^
+ O A K ^ = H B K ^ (cùng phụ A C B ^ )
+ HB = HK => H B K ^ = H K B ^
=> O K A ^ = H K B ^ ⇒ H K O ^ = 90 0
Đúng 2
Bình luận (0)