1. Cho tam giác ABC có diện tích bằng 24cm2, đường cao AH bằng 6 cm. Tính BC
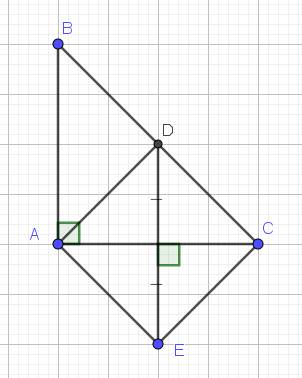
2. Cho tam giác ABC vuông cân tại A (AD là phân giác CD thuộc BC), E là điểm đối xứng với D qua AC. Tứ giác AECD là hình gì?
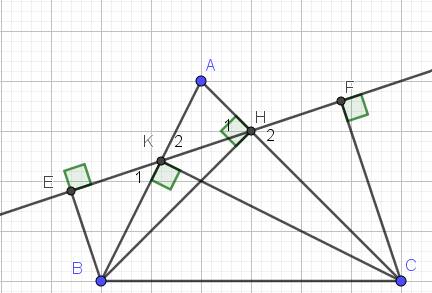
3. Cho tam giác nhọn ABC, các đường cao BH và CK. Gọi E và F lần lượt là hình chiếu của B và C trên HK. Chứng minh rằng EK = HF
Bài 2:
Tam giác $ABC$ cân tại $A$ nên phân giác $AD$ đồng thời là đường cao
$\Rightarrow AD\perp DC$. Mà $\widehat{DAC}=\widehat{BAC}:2 =45^0$ nên $\triangle DAC$ vuông cân tại $D$
$\Rightarrow DA=DC(1)$
$D,E$ đối xứng với nhau qua $AC$ nên $AC$ là trung trực của $DE$
$\Rightarrow CD=CE; AD=AE(2)$
Từ $(1); (2)\Rightarrow AD=DC=CE=EA$
$\Rightarrow ADCE$ là hình thoi.
Mà $\widehat{ADC}=90^0$ nên $ADCE$ là hình vuông.
Bài 3:
Xét tam giác $ABH$ và $ACK$ có:
$\widehat{AHB}=\widehat{AKC}=90^0$
$\widehat{A}$ chung
$\Rightarrow \triangle ABH\sim \triangle ACK$ (g.g)
$\Rightarrow \frac{AB}{AH}=\frac{AC}{AK}$
Xét tam giác $AKH$ và $ACB$ có:
$\widehat{A}$ chung
$\frac{AH}{AB}=\frac{AK}{AC}$ (cmt)
$\Rightarrow \triangle AKH\sim \triangle ACB$ (c.g.c)
$\Rightarrow \widehat{K_2}=\widehat{ACB}$ và $\widehat{H_1}=\widehat{ABC}$
Xét tam giác $KEB$ và $CHB$ có:
$\widehat{KEB}=\widehat{CHB}=90^0$
$\widehat{K_1}=\widehat{K_2}=\widehat{ACB}=\widehat{HCB}$ (cmt)
$\Rightarrow \triangle KEB\sim \triangle CHB$ (g.g)
$\Rightarrow \frac{KE}{KB}=\frac{CH}{CB}(1)$
Tương tự:
$\triangle CFH\sim \triangle CKB$ (c.g.c)
$\Rightarrow \frac{CH}{FH}=\frac{CB}{KB}(2)$
Từ $(1); (2)\Rightarrow \frac{KE}{KB}.\frac{CH}{FH}=\frac{CH}{CB}.\frac{CB}{KB}$
$\Rightarrow \frac{KE}{HF}=1$
$\Rightarrow KE=HF$ (đpcm)
Bài 1:
$BC=2S_{ABC}: AH=2.24:6=8$ (cm)