Ôn tập chương II - Đa giác. Diện tích đa giác
Nội dung lý thuyết
TÓM TẮT KIẾN THỨC CẦN NHỚ
1. Đa giác, đa giác đều và các công thức liên quan
a) Các định nghĩa
- Đa giác \(ABCDE\) là hình gồm các đoạn thẳng \(AB,BC,CD,DE,AE\), trong đó bất kì hai đoạn thẳng nào có một điểm chung đều không cùng nằm trên một đường thẳng.
- Đa giác lồi là đa giác luôn nằm trong nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác.
- Đa giác đều là đa giác có tất cả các cạnh bằng nhau, tất cả các góc bằng nhau.
b) Các công thức
- Số đường chéo của một hình \(n\) - giác là: \(\dfrac{n\left(n-3\right)}{2}\).
- Tổng các góc trong một hình \(n\) - giác là: \(\left(n-2\right).180^0\).
- Số đo mỗi góc trong một đa giác đều \(n\) cạnh là: \(\dfrac{\left(n-2\right).180^0}{n}\).
- Xét đa giác đều \(n\) cạnh:
| Số trục đối xứng | Số tâm đối xứng | |
| \(n\) chẵn | \(n\) | 1 |
| \(n\) lẻ | \(n\) | 0 |
2. Các công thức tính diện tích
| Hình | Kích thước | Công thức diện tích |
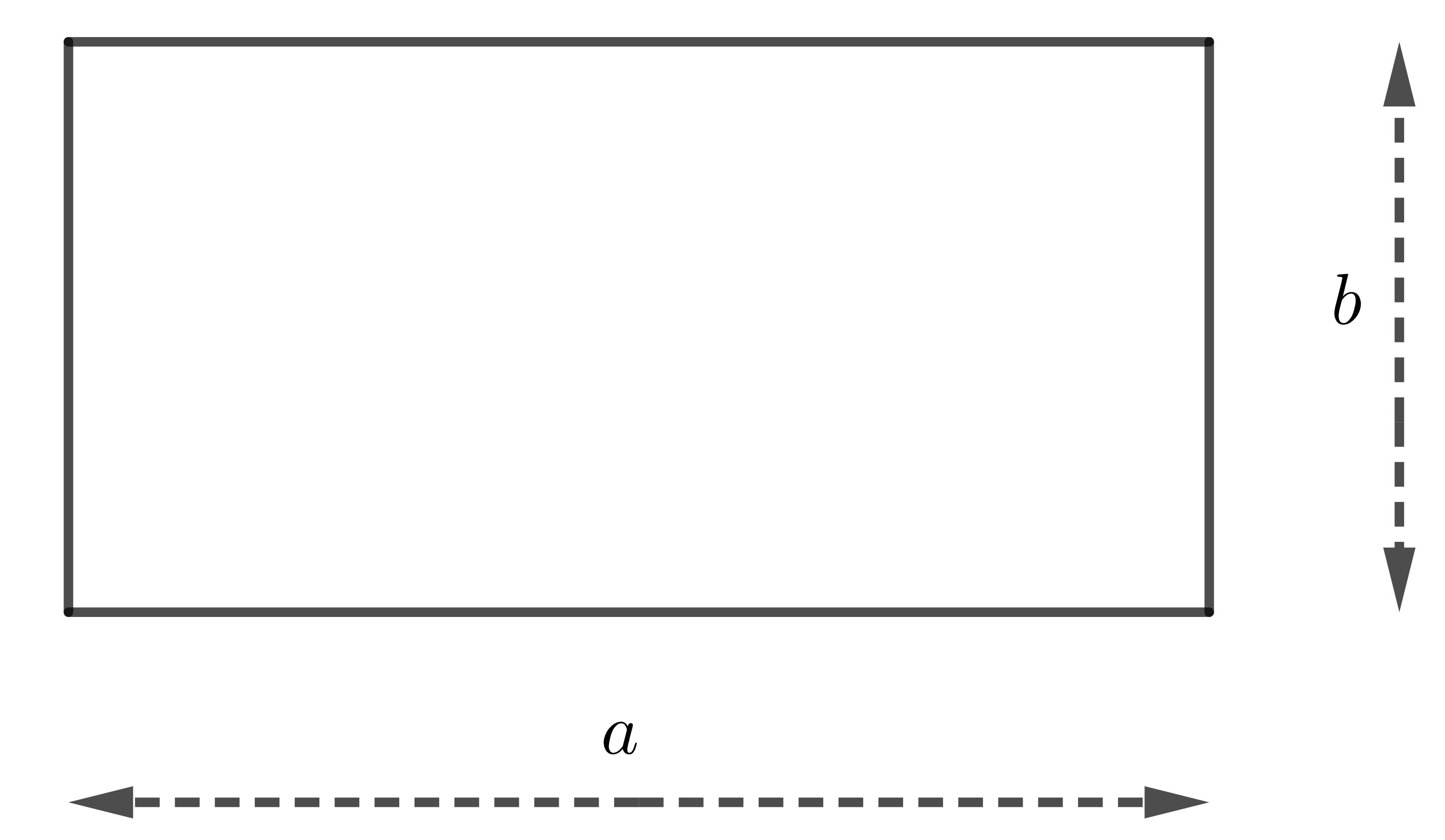
| Hình chữ nhật |
| \(S=ab\) |
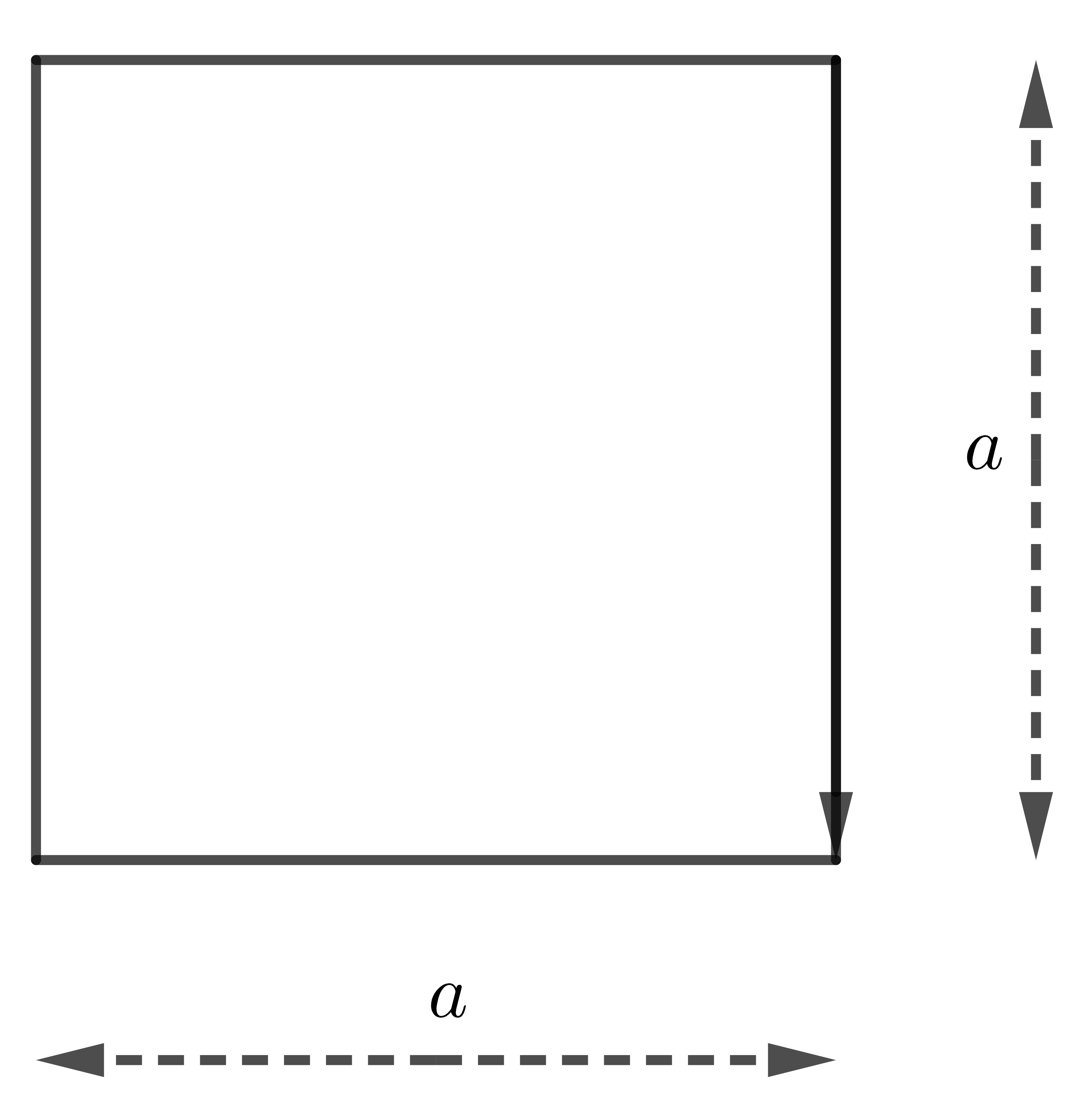
| Hình vuông |
| \(S=a^2\) |
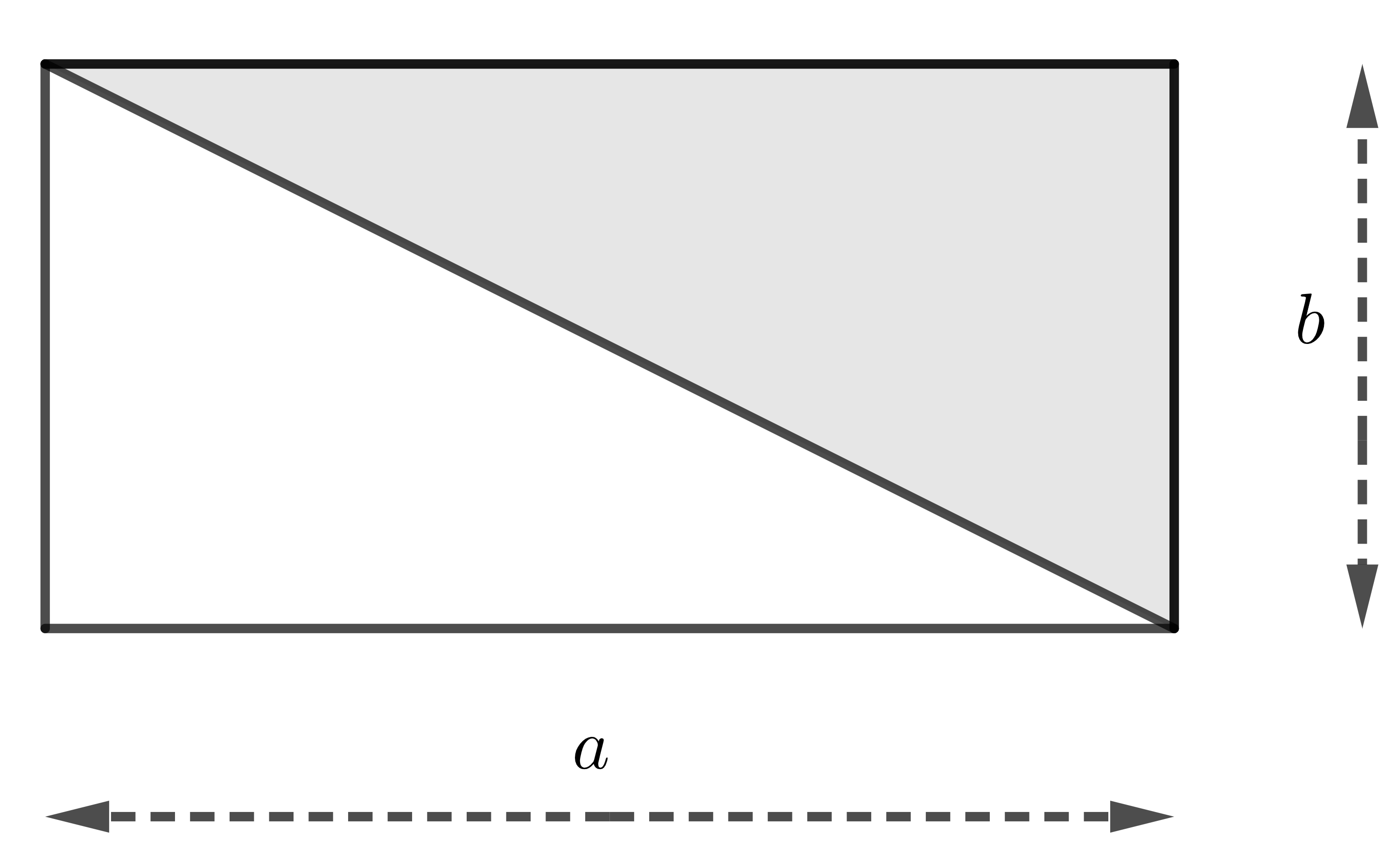
| Tam giác vuông |
| \(S=\dfrac{1}{2}ab\) |
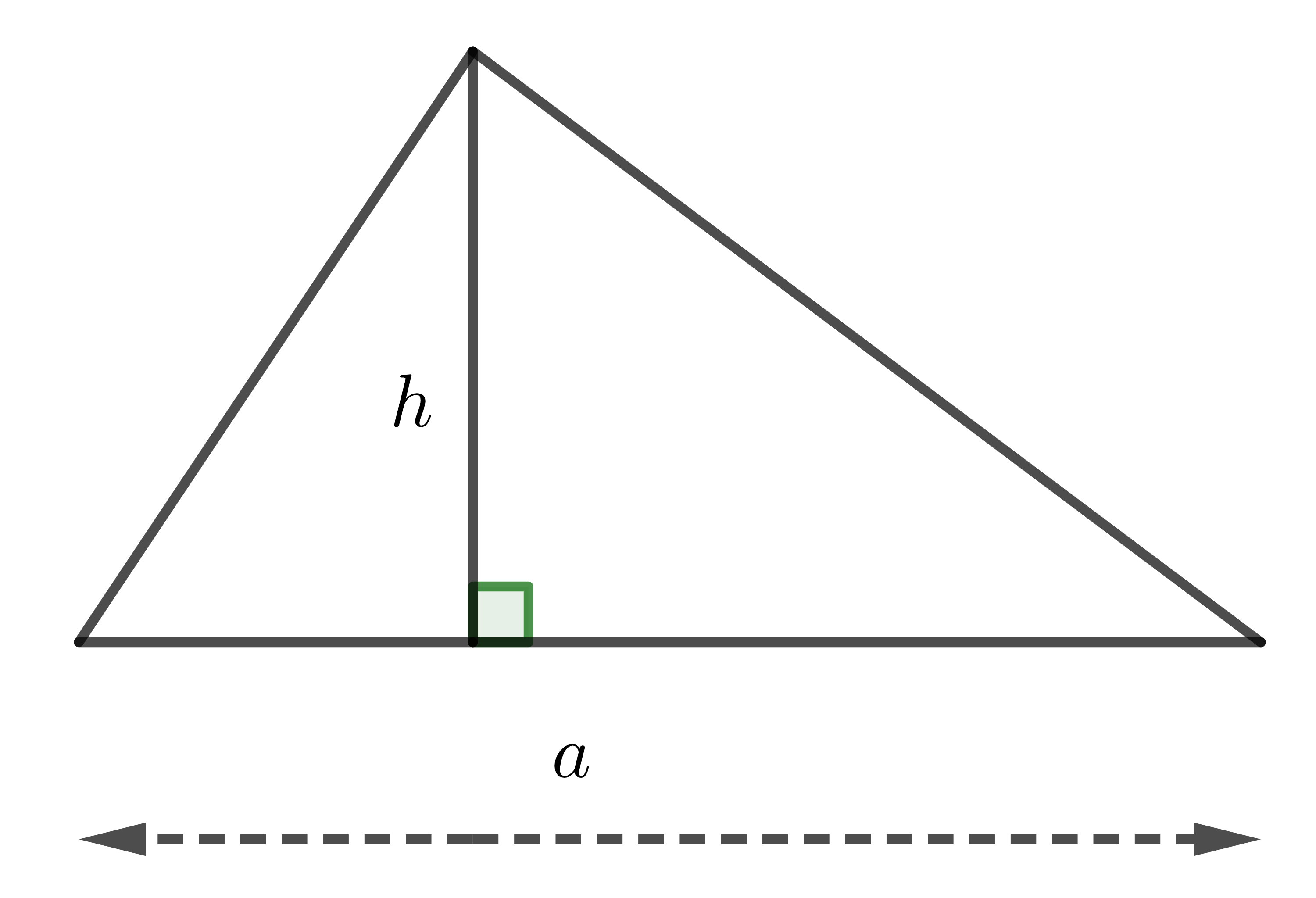
| Tam giác thường |
| \(S=\dfrac{1}{2}ah\) |
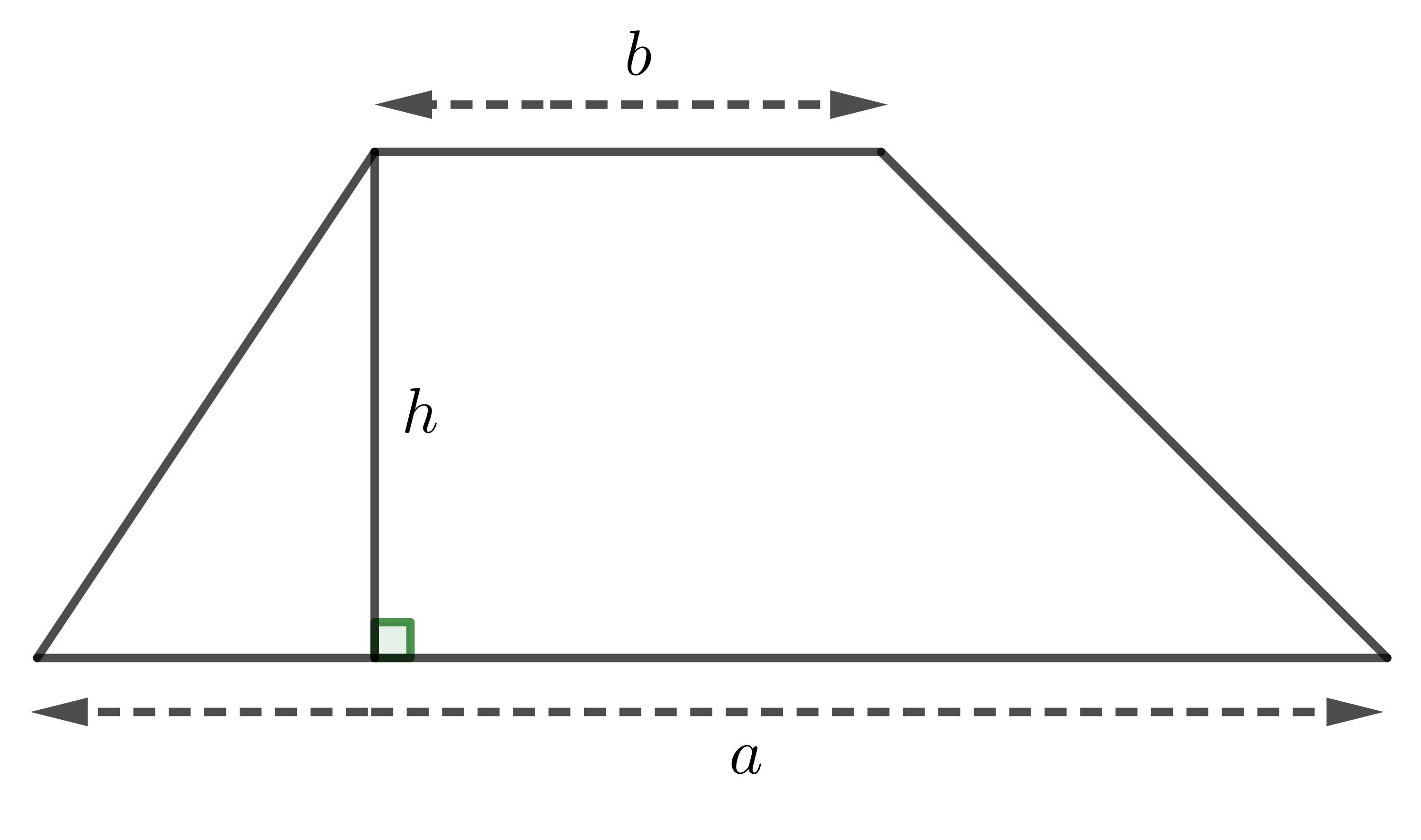
| Hình thang |
| \(S=\dfrac{1}{2}\left(a+b\right)h\) |
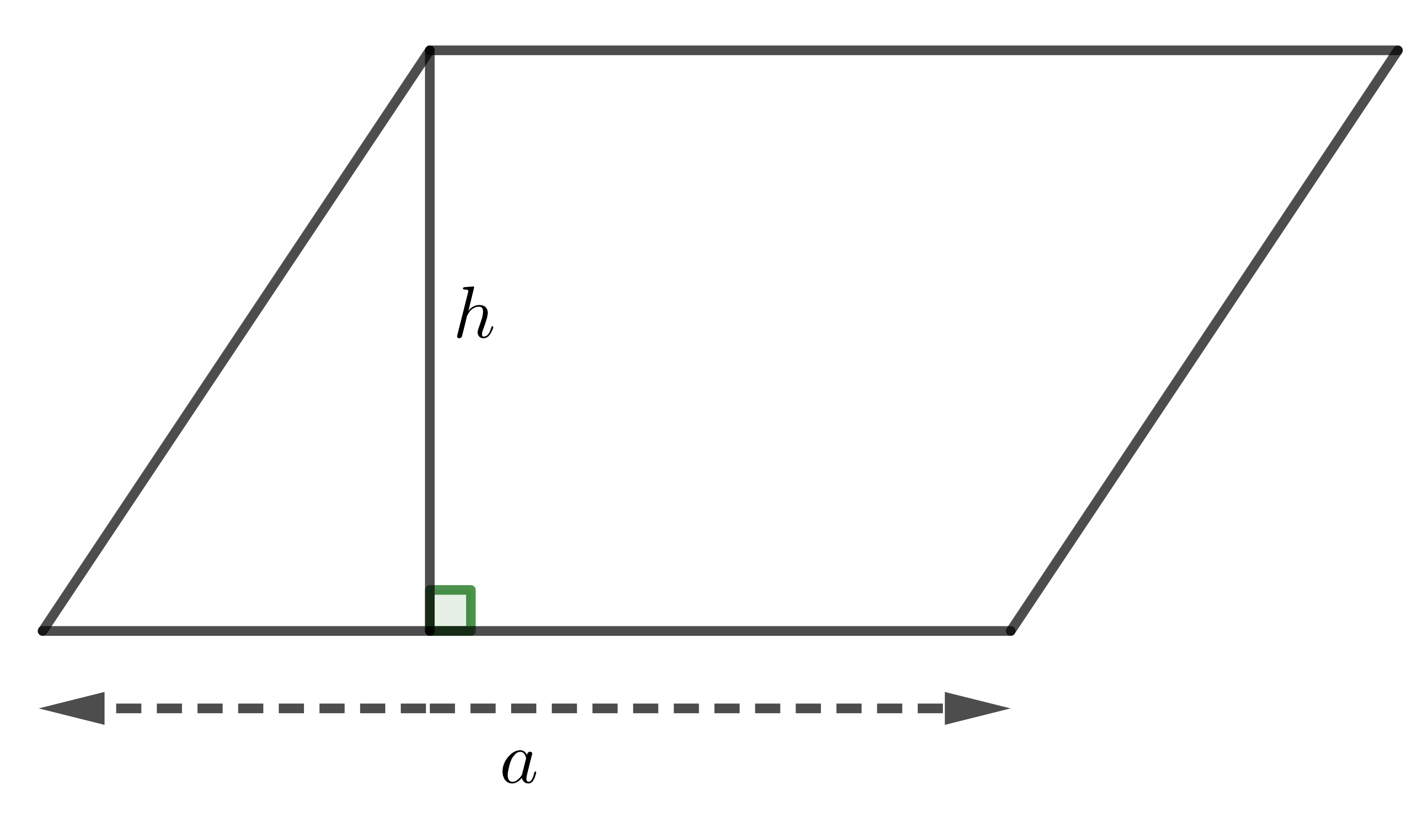
| Hình bình hành |
| \(S=ah\) |
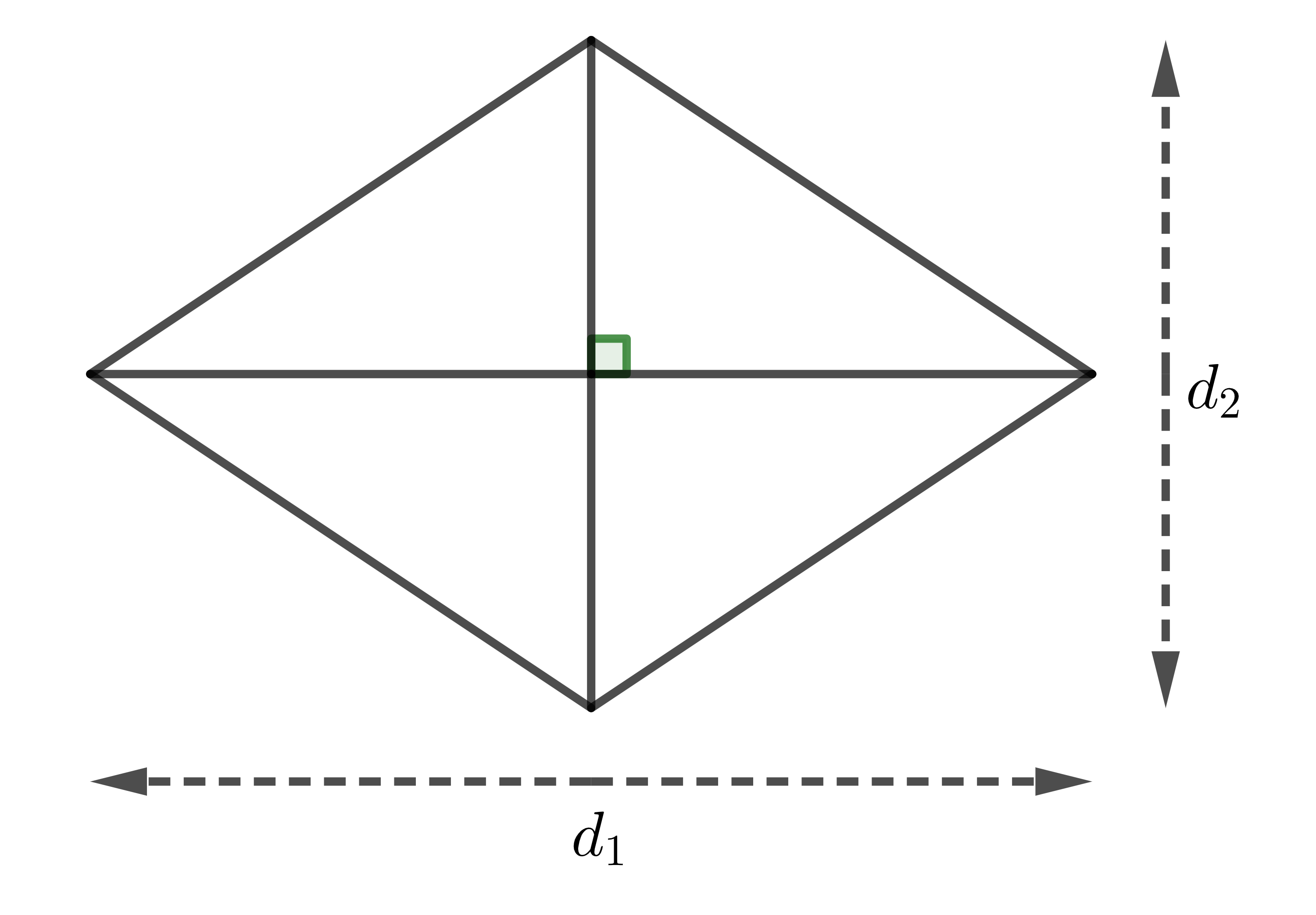
| Hình thoi |
| \(S=\dfrac{1}{2}d_1d_2\) |
@669221@