Bài 6: Diện tích đa giác

Ở các bài học trước, ta đã học công thức tính diện tích của tam giác và của các tứ giác đặc biệt: hình chữ nhật, hình thang, hình bình hành, hình thoi. 

Câu hỏi đặt ra là: Vậy với một đa giác bất kì, ta có thể tính diện tích của nó như thế nào?

Thông thường, để tính diện tích một đa giác, ta có thể thực hiện theo các phương pháp:

• Chia đa giác thành các tam giác.

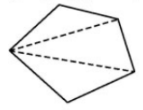
• Tạo ra một tam giác nào đó chứa đa giác.

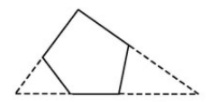
• Chia đa giác thành nhiều tam giác vuông và hình thang vuông.

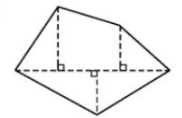
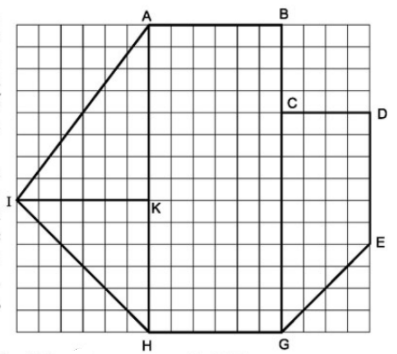
Ví dụ: Tính diện tích đa giác \(ABCDEGHI\) sau, coi mỗi ô vuông nhỏ có cạnh bằng 1.

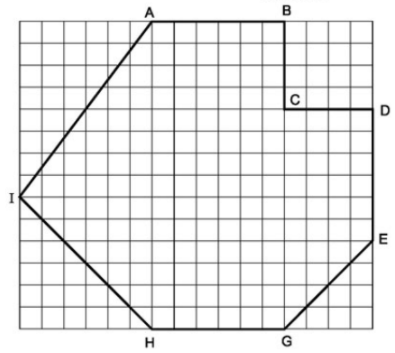
Lời giải: 

Để tính diện tích đa giác \(ABCDEGHI\), ta chia nó thành 3 phần: tam giác \(AHI\), hình chữ nhật \(ABGH\) và hình thang vuông \(CDEG\).

Xét tam giác \(AHI\), ta có:

• Đáy \(AH=14\) (đơn vị).
• Chiều cao \(IK=6\) (đơn vị).

\(\Rightarrow S_{AHI}=\dfrac{1}{2}AH.IK=\dfrac{1}{2}.14.6=42\) (đơn vị diện tích).

Xét hình chữ nhật \(ABGH\) có: 

• Chiều dài \(AH=BG=14\) (đơn vị).
• Chiều rộng \(AB=GH=6\) (đơn vị).

\(\Rightarrow S_{ABGH}=AB.BG=14.6=84\) (đơn vị diện tích).

Xét hình thang vuông \(CDEG\) có:

• Đáy lớn \(CG=10\) (đơn vị); đáy nhỏ \(ED=6\) (đơn vị).
• Chiều cao \(CD=4\) (đơn vị).

\(\Rightarrow S_{CDEG}=\dfrac{1}{2}\left(CG+DE\right).CD=\dfrac{1}{2}\left(10+6\right).4=32\) (đơn vị diện tích).

Vậy, diện tích đa giác \(ABCDEGHI\) là:

\(S_{ABCDEGHI}=S_{AHI}+S_{ABGH}+S_{CDEG}=42+84+32=158\) (đơn vị diện tích).