Bài 5: Diện tích hình thoi
Nội dung lý thuyết
1. Diện tích tứ giác có hai đường chéo bằng nhau
Xét bài toán sau: Cho tứ giác \(ABCD\) có \(AC\perp BD\). Tính diện tích tứ giác \(ABCD\).
Gọi \(H\) là giao điểm \(AC\) và \(BD\). Ta có hình vẽ:
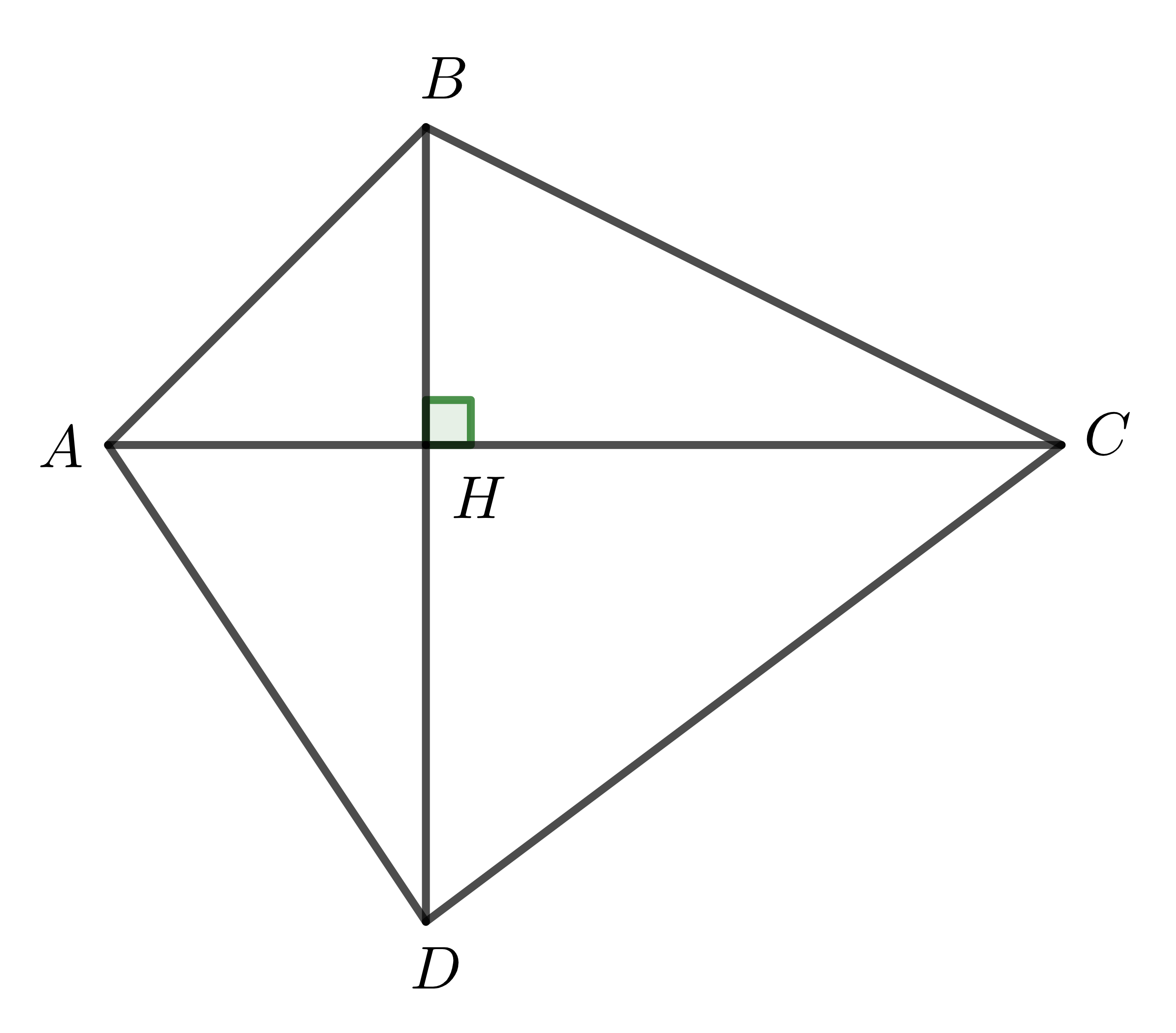
Dễ thấy, tứ giác \(ABCD\) được chia thành hai tam giác \(ABC\) và \(ADC\). Do đó:
\(S_{ABCD}=S_{ABC}+S_{ADC}\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}AC.BH+\dfrac{1}{2}AC.DH=\dfrac{1}{2}AC\left(BH+DH\right)=\dfrac{1}{2}AC.BD\)
Rõ ràng kết quả trên đúng với mọi tứ giác thỏa mãn tính chất hai đường chéo vuông góc. Từ đó ta có nhận xét sau:
Nhận xét: Tứ giác có hai đường chéo vuông góc với nhau thì diện tích của nó bằng nửa tích của hai đường chéo.
Ví dụ: Cho tứ giác \(ABCD\) có \(AC\perp BD\). Biết \(AC=6cm;BD=10cm\). Khi đó, ta tính được diện tích tứ giác \(ABCD\) là: \(S_{ABCD}=\dfrac{1}{2}AC.BD=\dfrac{1}{2}.6.10=30\left(cm^2\right)\).
2. Công thức tính diện tích hình thoi
Ở những bài trước ta đã biết, hình thoi là một tứ giác có hai đường chéo vuông góc. Do đó, diện tích hình thoi cũng được tính tương tự như một tứ giác bất kì có hai đường chéo vuông góc phía trên.
Định lí: Diện tích hình thoi bằng nửa tích của hai đường chéo.
\(S=\dfrac{1}{2}d_1.d_2\)
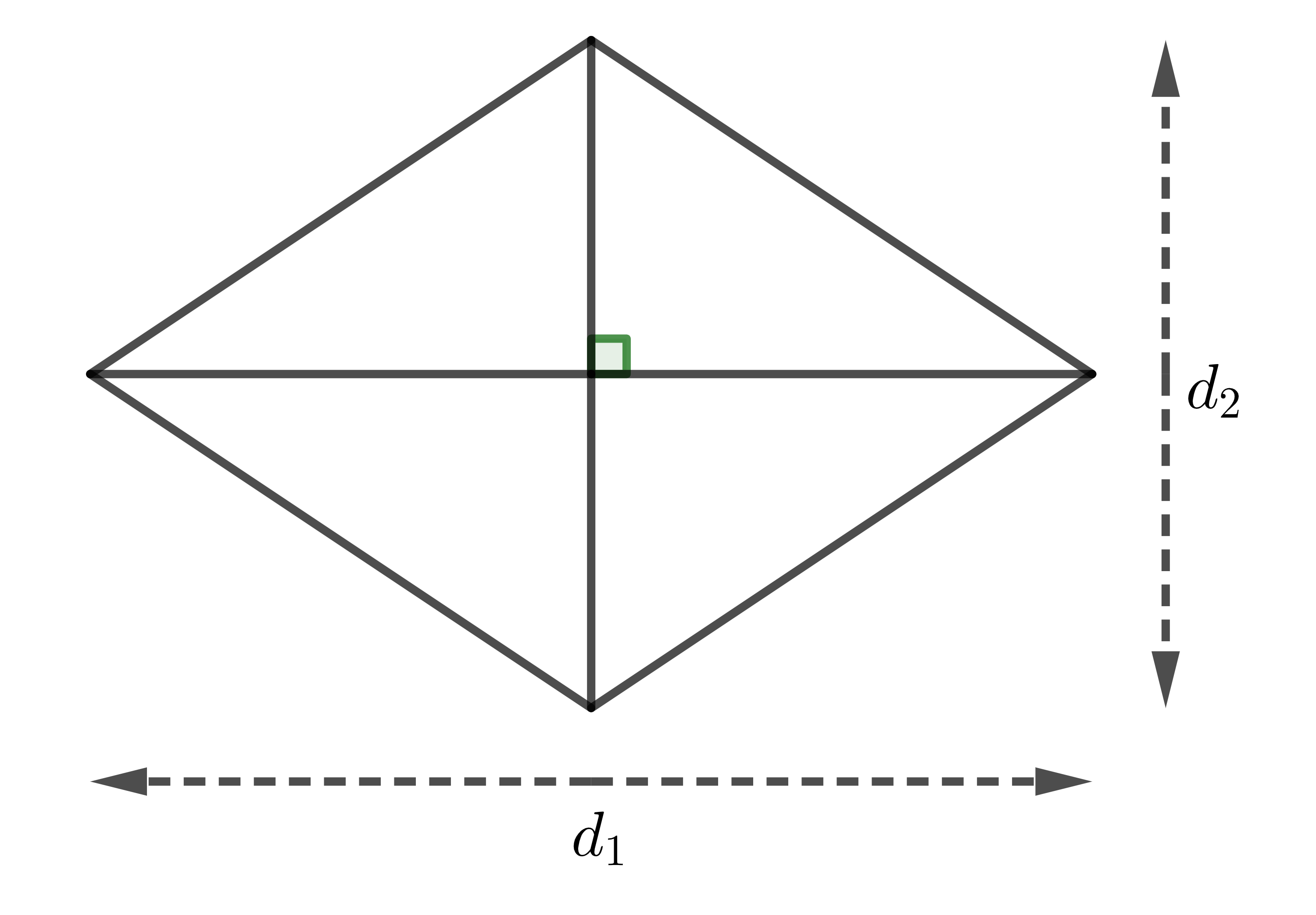
Nhận xét: Hình thoi cũng là một hình bình hành, do đó ta cũng có thể áp dụng công thức tính diện tích hình bình hành để tính diện tích hình thoi.
Ví dụ 1: Cho hình thoi \(ABCD\) có diện tích \(20cm^2\). Biết \(AC=4cm\). Tính độ dài đường chéo \(BD\).
Lời giải:
Ta có: \(S_{ABCD}=\dfrac{1}{2}AC.BD\Rightarrow BD=\dfrac{2S_{ABCD}}{AC}=\dfrac{2.20}{4}=10\left(cm\right)\).
Vậy đường chéo \(BD\) dài \(10cm\).
Ví dụ 2: Cho hình thoi \(ABCD\) có diện tích \(24cm^2\). Biết hai đường chéo có tỉ lệ \(\dfrac{AC}{BD}=\dfrac{3}{4}\). Tính độ dài cạnh hình thoi.
Lời giải:
Do \(\dfrac{AC}{BD}=\dfrac{3}{4}\Rightarrow AC=\dfrac{3}{4}BD\).
Ta có: \(S_{ABCD}=\dfrac{1}{2}AC.BD=\dfrac{1}{2}.\dfrac{3}{4}BD^2=\dfrac{3}{8}BD^2\)
\(\Rightarrow24=\dfrac{3}{8}BD^2\Rightarrow BD^2=24:\dfrac{3}{8}=64\Rightarrow BD=8\left(cm\right)\)
\(\Rightarrow AC=\dfrac{3}{4}.BD=\dfrac{3}{4}.8=6\left(cm\right)\).
Gọi \(AC\cap BD\equiv O\). Theo tính chất hình thoi, ta có \(O\) là trung điểm \(AC,BD\).
\(\Rightarrow OA=\dfrac{1}{2}AC=\dfrac{1}{2}.6=3\left(cm\right);OB=\dfrac{1}{2}BD=\dfrac{1}{2}.8=4\left(cm\right)\).
Do tam giác \(OAB\) vuông tại \(O\) (tính chất hình thoi).
Áp dụng định lí Pytago ta có: \(AB^2=OA^2+OB^2=3^2+4^2=25\)
\(\Rightarrow AB=5\left(cm\right)\).
Vậy cạnh của hình thoi \(ABCD\) là \(5cm\).
@58061@
3. Ví dụ
Xét ví dụ sau: Cho hình thang cân \(ABCD\) (\(AB\)//\(CD\)). Biết \(AB=3cm;CD=5cm\) và diện tích hình thang là \(8cm^2\). Gọi \(M,E,N,G\) lần lượt là trung điểm \(AD,AB,BC,CD\).
a) Tứ giác \(MENG\) là hình gì?
b) Tính diện tích tứ giác \(MENG\).
Lời giải:
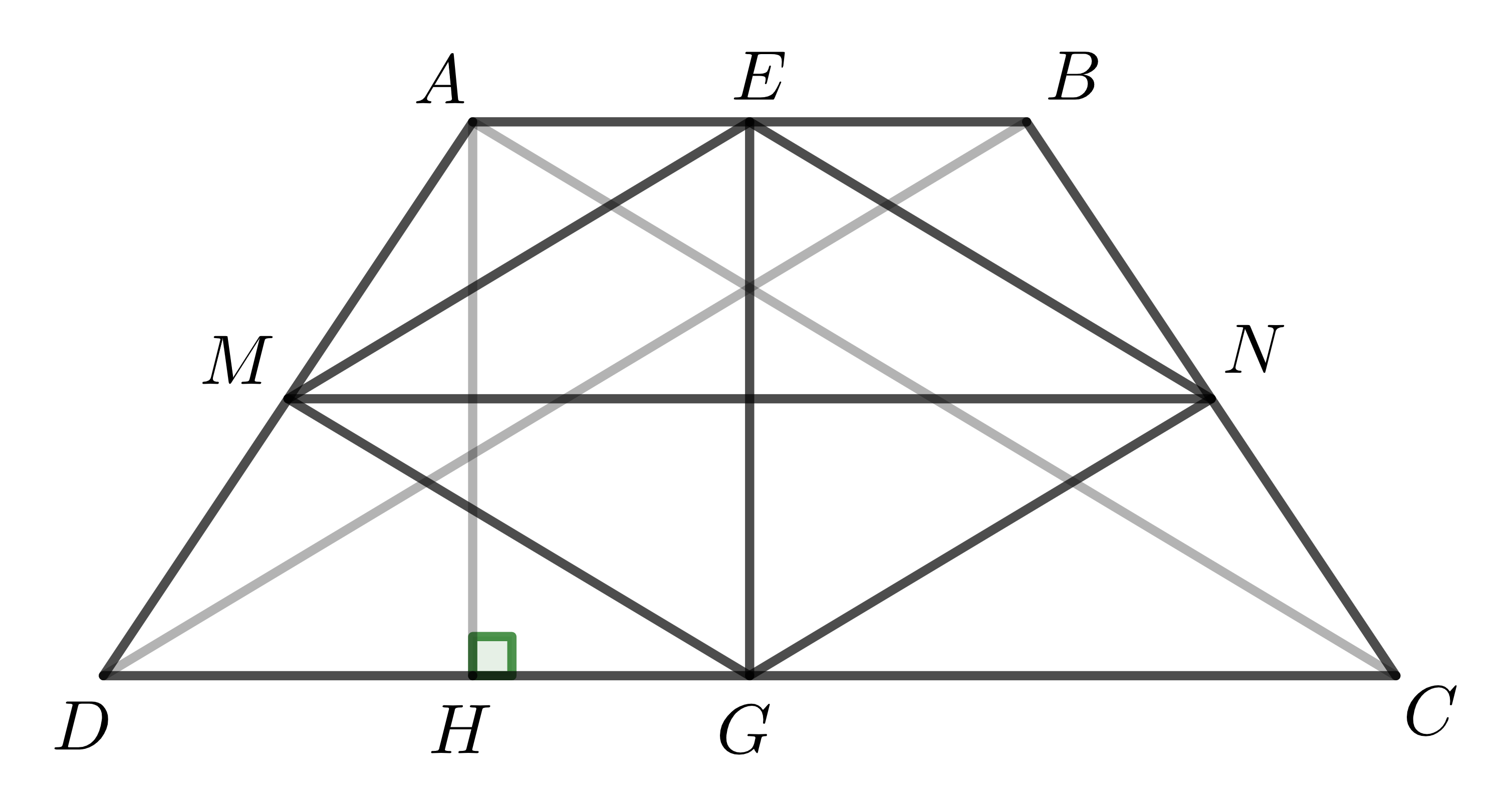
a) Ta có \(\left\{ \begin{array} $ME \parallel BD; ME=\dfrac{1}{2}BD \\ NG\parallel BD; NG=\dfrac{1}{2}BD \end{array}\right.\) \(\Rightarrow ME\parallel NG; ME=NG=\dfrac{1}{2}BD\).
\(\Rightarrow MENG\) là hình bình hành.
Tương tự ta cũng có \(EN\parallel MG; EN=MG=\dfrac{1}{2}AC\).
Mà \(AC=BD\) (tính chất hình thang cân) \(\Rightarrow ME=EN=NG=MG\Rightarrow MENG\) là hình thoi.
b) Ta có \(M,N\) là trung điểm \(AD,BC\) nên \(MN\) là đường trung bình của hình thang \(ABCD\)
\(\Rightarrow MN=\dfrac{AB+CD}{2}=\dfrac{3+5}{2}=4\left(cm\right)\).
Mặt khác, ta có: \(S_{ABCD}=8\left(cm^2\right)\Rightarrow\dfrac{1}{2}\left(AB+CD\right).AH=8\)
\(\Rightarrow AH=\dfrac{8.2}{3+5}=2\left(cm\right)\).
Dễ thấy \(EG\) cũng là đường cao của hình thang \(ABCD\) nên \(EG=AH=2\left(cm\right)\).
Như vậy, diện tích hình thoi \(MENG\) là:
\(S_{MENG}=\dfrac{1}{2}MN.EG=\dfrac{1}{2}.4.2=4\left(cm^2\right).\)