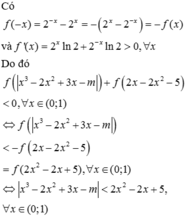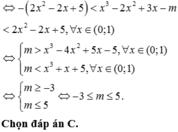Cm : 2x-2x2-1 < 0 với mọi x

Những câu hỏi liên quan
CM các bất phương trình sau luôn dương vs mọi x
1)2x2-2x+17>0
2)-x2+6x-18<0
3)|x-1|+|x|+2>1
BPT thì làm sao gọi là luôn dương hả bạn? Đề phải là CMR các BPT sau luôn đúng với mọi $x$.
1.
Ta có: $2x^2-2x+17=x^2+(x^2-2x+1)+16=x^2+(x-1)^2+16\geq 16>0$ với mọi $x\in\mathbb{R}$
Do đó BPT luôn đúng với mọi $x$
2.
$-x^2+6x-18=-(x^2-6x+18)=-[(x^2-6x+9)+9]=-[(x-3)^2+9]$
$=-9-(x-3)^2\leq -9<0$ với mọi $x\in\mathbb{R}$
Vậy BPT luôn đúng với mọi $x$
3.
$|x-1|+|x|+2\geq 0+0+2=2>1$ với mọi $x\in\mathbb{R}$
Do đó BPT luôn đúng với mọi $x$
Đúng 0
Bình luận (0)
Chứng minh rằng:
a) x2 + x + 1 > 0 với mọi x
b)4y2 + 2y + 1 > 0 với mọi y
c) -2x2 + 6x - 10 < 0 với mọi x
a: \(x^2+x+1=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall x\)
b: \(4y^2+2y+1\)
\(=4\left(y^2+\dfrac{1}{2}y+\dfrac{1}{4}\right)\)
\(=4\left(y^2+2\cdot y\cdot\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{3}{16}\right)\)
\(=4\left(y+\dfrac{1}{4}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall y\)
c: \(-2x^2+6x-10\)
\(=-2\left(x^2-3x+5\right)\)
\(=-2\left(x^2-3x+\dfrac{9}{4}+\dfrac{11}{4}\right)\)
\(=-2\left(x-\dfrac{3}{2}\right)^2-\dfrac{11}{2}< =-\dfrac{11}{2}< 0\forall x\)
Đúng 1
Bình luận (0)
`#3107.101107`
a)
`x^2 + x + 1`
`= (x^2 + 2*x*1/2 + 1/4) + 3/4`
`= (x + 1/2)^2 + 3/4`
Vì `(x + 1/2)^2 \ge 0` `AA` `x`
`=> (x + 1/2)^2 + 3/4 \ge 3/4` `AA` `x`
Vậy, `x^2 + x + 1 > 0` `AA` `x`
b)
`4y^2 + 2y + 1`
`= [(2y)^2 + 2*2y*1/2 + 1/4] + 3/4`
`= (2y + 1/2)^2 + 3/4`
Vì `(2y + 1/2)^2 \ge 0` `AA` `y`
`=> (2y + 1/2)^2 + 3/4 \ge 3/4` `AA` `y`
Vậy, `4y^2 + 2y + 1 > 0` `AA` `y`
c)
`-2x^2 + 6x - 10`
`= -(2x^2 - 6x + 10)`
`= -2(x^2 - 3x + 5)`
`= -2[ (x^2 - 2*x*3/2 + 9/4) + 11/4]`
`= -2[ (x - 3/2)^2 + 11/4]`
`= -2(x - 3/2)^2 - 11/2`
Vì `-2(x - 3/2)^2 \le 0` `AA` `x`
`=> -2(x - 3/2)^2 - 11/2 \le 11/2` `AA` `x`
Vậy, `-2x^2 + 6x - 10 < 0` `AA `x.`
Đúng 0
Bình luận (0)
Cho hàm số
f
x
2
x
-
2
-
x
. Có bao nhiêu số nguyên m để bất phương trình
f
x
3
-
2
x
2
+
3
x...
Đọc tiếp
Cho hàm số f x = 2 x - 2 - x . Có bao nhiêu số nguyên m để bất phương trình f x 3 - 2 x 2 + 3 x - m + f 2 x - 2 x 2 - 5 < 0 có nghiệm đúng với mọi x ∈ 0 ; 1 .
A. 7.
B. 3.
C. 9.
D. 5.
Cm 2x2-6x+15 > 0 vs mọi x
Ta có : \(2x^2-6x+15\)
\(=2\left(x^2-2.x.\frac{3}{2}+\frac{9}{4}\right)+\frac{21}{2}\)
\(=2\left(x-\frac{3}{2}\right)^2+\frac{21}{2}>0\)
Cm 2x-2x2-1<0 với mọi số thực x
\(2x-2x^2-1\)
=\(2\left(x-x^2-\dfrac{1}{2}\right)\)
= \(2\left(-x^2+2.\dfrac{1}{2}x-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{2}\right)\)
= \(2\left[\left(-x^2+2.\dfrac{1}{2}x-\dfrac{1}{4}\right)-\dfrac{1}{4}\right]\)
=\(2\left(-x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}\right)-\dfrac{1}{2}\)
= \(-2\left(x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}\right)-\dfrac{1}{2}\)
= \(\dfrac{-1}{2}-2\left(x-\dfrac{1}{2}\right)^2\)
vậy \(2x-2x^2-1< 0\) với mọi số thực x
Đúng 0
Bình luận (1)
Giúp mình : CM: 2x^8 + 2x^7 +1 >0 với mọi x.
Cho bất phương trình
2
−
x
2
+
2
x
+
1
+
2
x
2
−
2
x
≥
m
.
Tìm m để bất phương trình đúng với mọi
x
∈...
Đọc tiếp
Cho bất phương trình 2 − x 2 + 2 x + 1 + 2 x 2 − 2 x ≥ m . Tìm m để bất phương trình đúng với mọi x ∈ ℝ
A. m ≤ 3
B. m ≥ 3 2
C. m ≤ 2 2
D. m ≤ 3 2
Đáp án C
Đặt t = 2 x 2 − 2 x , t ∈ 0 ; + ∞ ⇒ B P T ⇔ 2 t + t ≥ m 1
Ta có t + 2 t ≥ 2 t . 2 t = 2 2 ⇒ 1 ⇔ m ≤ 2 2
Đúng 0
Bình luận (0)
cm x^4-2x^3+2x^2-2x+1> hoặc bằng 0 với mọi giá trị của x
Tính giá trị của phân thức:a)
x
2
−
2
x
−
3
x
2
+
2
x
+
1
với
x
≠
−
1
tại
3
x
−
1...
Đọc tiếp
Tính giá trị của phân thức:
a) x 2 − 2 x − 3 x 2 + 2 x + 1 với x ≠ − 1 tại 3 x − 1 = 0 ;
b) x − 2 x 2 − 5 x + 6 với x ≠ 2 ; x ≠ 3 tại x 2 − 4 = 0 .