Cho tam giác MNI.vẽ đường tròn đường kính NI cắt MN và MI lần lượt tại D,E.
a. Chứng minh NE vuông góc với MI , ID vuông góc với MN
b. Gọi H là giao điểm của NE và ID.Chứng minh MH vuông góc với NI

Những câu hỏi liên quan
Cho tam giác MNI.vẽ đường tròn đường kính NI cắt MN và MI lần lượt tại D,E.
a. Chứng minh NE vuông góc với MI , ID vuông góc với MN
b. Gọi H là giao điểm của NE và ID.Chứng minh MH vuông góc với NI
a: Xét (O) có
ΔNEI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNEI vuông tại E
hay NE⊥MI
Xét (O) có
ΔNDI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNDI vuông tại D
hay ID⊥MN
b: Xét ΔMNI có
ID là đường cao ứng với cạnh MN
NE là đường cao ứng với cạnh MI
NE cắt ID tại H
Do đó: MH⊥NI
Đúng 1
Bình luận (0)
Cho tam giác MNI.vẽ đường tròn đường kính NI cắt MN và MI lần lượt tại D,E.
a. Chứng minh NE vuông góc với MI , ID vuông góc với MN
b. Gọi H là giao điểm của NE và ID.Chứng minh MH vuông góc với NI
\(a,\)Gọi tâm đường tròn đường kính NI là O
Ta có \(OE=OD=ON=OI\left(=R\right)=\dfrac{1}{2}IN\)
\(\Rightarrow\Delta INE,\Delta IND\) lần lượt vuông tại \(E,D\)
\(\Rightarrow NE\perp MI,ID\perp MN\)
\(b,\) Tam giác MNI có NE, ID là đường cao; H là giao điểm NE và ID nên H là trực tâm
\(\Rightarrow MH\) là đường cao thứ 3
\(\Rightarrow MH\perp NI\)
Đúng 4
Bình luận (0)
Cho tam giác MNI.vẽ đường tròn đường kính NI cắt MN và MI lần lượt tại D,E.a. Chứng minh NE vuông góc với MI , ID vuông góc với MNb. Gọi H là giao điểm của NE và ID.Chứng minh MH vuông góc với NI Cho tam giác ABC nối tiếp (O;R).Tính độ dài các cạnh AB,AC,biết R 3cm và khoảng cách từ O đến AB,AC lần lượt là 2sqrt{2} và dfrac{sqrt{11}}{2}cm
Đọc tiếp
Cho tam giác MNI.vẽ đường tròn đường kính NI cắt MN và MI lần lượt tại D,E.
a. Chứng minh NE vuông góc với MI , ID vuông góc với MN
b. Gọi H là giao điểm của NE và ID.Chứng minh MH vuông góc với NI
Cho tam giác ABC nối tiếp (O;R).Tính độ dài các cạnh AB,AC,biết R = 3cm và khoảng cách từ O đến AB,AC lần lượt là 2\(\sqrt{2}\) và \(\dfrac{\sqrt{11}}{2}\)cm
Câu 1:
a: Xét (\(\dfrac{NI}{2}\)) có
ΔNEI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNEI vuông tại E
Xét \(\left(\dfrac{NI}{2}\right)\) có
ΔNDI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNDI vuông tại D
b: Xét ΔMNI có
NE là đường cao ứng với cạnh MI
ID là đường cao ứng với cạnh MN
NE cắt ID tại H
Do đó: MH\(\perp\)NI
Đúng 2
Bình luận (0)
Cho tam giác MNI.vẽ đường tròn đường kính NI cắt MN và MI lần lượt tại D,E.
a. Chứng minh NE vuông góc với MI , ID vuông góc với MN
b. Gọi H là giao điểm của NE và ID.Chứng minh MH vuông góc với NI
a: Xét (O) có
ΔNEI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNEI vuông tại E
Xét (O) có
ΔNDI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNDI vuông tại D
HT , đúng thì k nhé
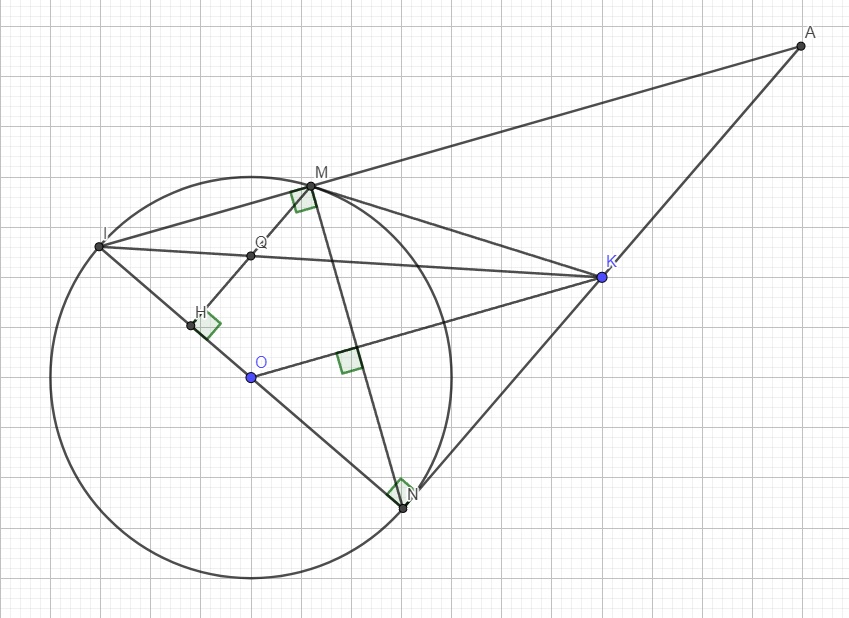
Cho đường tròn (O;R), dây MN khác đường kính. Hai tiếp tuyến của đường tròn (O;R) tại M và N cắt nhau tại K. Kẻ đường kính NI, kẻ MH vuông góc với NI tại H. a) chứng minh OK vuông góc với ON b) chứng minh ON là phân giác góc HMK c) gọi Q là giao điểm của KI và MH. Chứng minh QH = QM
Đề bài sai nhiều quá, em kiểm tra lại câu a là ON hay MN, và câu b là ON hay MN?
Đúng 0
Bình luận (1)
a.
Ta có: \(KM=KN\) (t/c hai tiếp tuyến cắt nhau)
\(OM=ON=R\)
\(\Rightarrow OK\) là trung trực của MN, hay \(OK\perp MN\)
b.
Có \(\widehat{KMN}=\widehat{KNM}\) (do \(\Delta KMN\) cân tại K)
\(\widehat{KNM}=\widehat{HMN}\) (cùng phụ \(\widehat{HNM}\))
\(\Rightarrow\widehat{KMN}=\widehat{HMN}\)
\(\Rightarrow MN\) là phân giác \(\widehat{HMK}\)
c.
Kéo dài IM và NK cắt nhau tại A
Theo câu ta có \(OK\perp MN\Rightarrow OK||IA\) (cùng vuông góc MN)
Mà O là trung điểm IN \(\Rightarrow K\) là trung điểm AN
Hay \(KA=KN\) (1)
Do \(MH||AN\) (cùng vuông góc IN), áp dụng định lý Talet trong tam giác KIN:
\(\dfrac{IQ}{IK}=\dfrac{QH}{KN}\) (2)
Áp dụng định lý Talet trong tam giác AIK:
\(\dfrac{IQ}{IK}=\dfrac{QM}{KA}\) (3)
(1);(2);(3) \(\Rightarrow QH=QM\)
Đúng 0
Bình luận (0)
cho đường tròn(O;6cm) đường kính AB.Trên đường tròn lấy điểm M sao cho AM =4cm.Kẻ dây MN vuông góc AB tại I(I thuộc AB)
a,chứng minh tam giác AMB vuông và tính độ dài MI)
b,Gọi E đối xứng với A qua I,F là giao điểm của đường thẳng NE và ME.Chứng minh NF song song với AM
c,Chứng minh F thuộc đường tròn đường kính BE và FI là tiếp tuyến của đường tròn đường kính BE
cho tam giác MNP vuông tại M . MN = 4cm, MP = 3cm. đường cao MI : a) Cm tam giác MNP và tam giác INM đồng dang => MN mũ 2 = NP . NI; b) tính độ dài NI và IP : c) gọi NE là tia phân giác của góc MNP . K là giao điểm NE và MI. cm EM/EP, NI/MN ; d) kẻ IH vuong góc với MN tại H. tính diện tích tam giác IMH
Cho tam giác MNK cân tại M ( góc M nhỏ hơn 90độ ) .Vẽ NI vuông góc MK tại I , KP vuông góc MN tại P . Chứng minh rằng MI = MP . Gọi H là giao điểm của NI và PK Chứng minh MH là phân giác của góc M . Chứng minh PI song song NK
a) Xét tam giác PNK vuông tại P và tam giác INK vuông tại I có:
\(\widehat{N}=\widehat{K}\)(tam giác MNK là tam giác cân)
NK:chung
Suy ra \(\Delta PNK=\Delta INK\)(cạnh huyền-góc nhọn)
=>PN=IK(1)
Mà do MNK cân tại M nên MN=MK(2)
Từ (1) và (2), suy ra MI=MP
b)Từ a) ta suy ra: \(\widehat{HNK}=\widehat{HKN}\)(hai góc tương ứng)<=> \(\widehat{IKH}=\widehat{PNH}\)
Xét tam giác PHN vuông tại P và tam giác IHK vuông tại I có:
\(NP=IK\left(cmt\right)\)
\(\widehat{IKH}=\widehat{PNH}\)(cmt)
Suy ra:....(cạnh góc vuông-góc nhọn kề)
=>HP=HI
Xét tam giác PMH và tam giác HMI có:
MH:chung
MP=MI(cmt)
HP=HI(cmt)
Suy ra:....(c-c-c)
=> \(\widehat{PMH}=\widehat{IMH}\)(hai góc tương ứng )
=>MH là tia phân giác của góc M
c) Từ b) suy ra MP=MI(2 cạnh tương ứng)
=>PMI là tam giác cân
Xét tam giác PMI có:
\(\widehat{P}=\widehat{I}=\frac{180^o-\widehat{M}}{2}\left(1\right)\)
Xét tam giác MNK có:
\(\widehat{K}=\widehat{N}=\frac{180^o-\widehat{M}}{2}\left(2\right)\)
=>\(\widehat{K}=\widehat{N}=\widehat{P}=\widehat{I}\)
Mà các cặp góc này ở vị trí đồng vị nên PI//NK
Cho ∆MNP vuông tại M có MN< MP. Kẻ đường phân giác NI của góc MNP ( I thuộc MP) .kẻ IK vuông góc NP a. Chứng minh rằng ∆IMN=∆IKN b. chứng minh rằng MI < IP c. Gọi Q là giao điểm của IK và MN , đường thẳng NI cắt QP tại D. Chứng minh rằng ND vuông góc QP
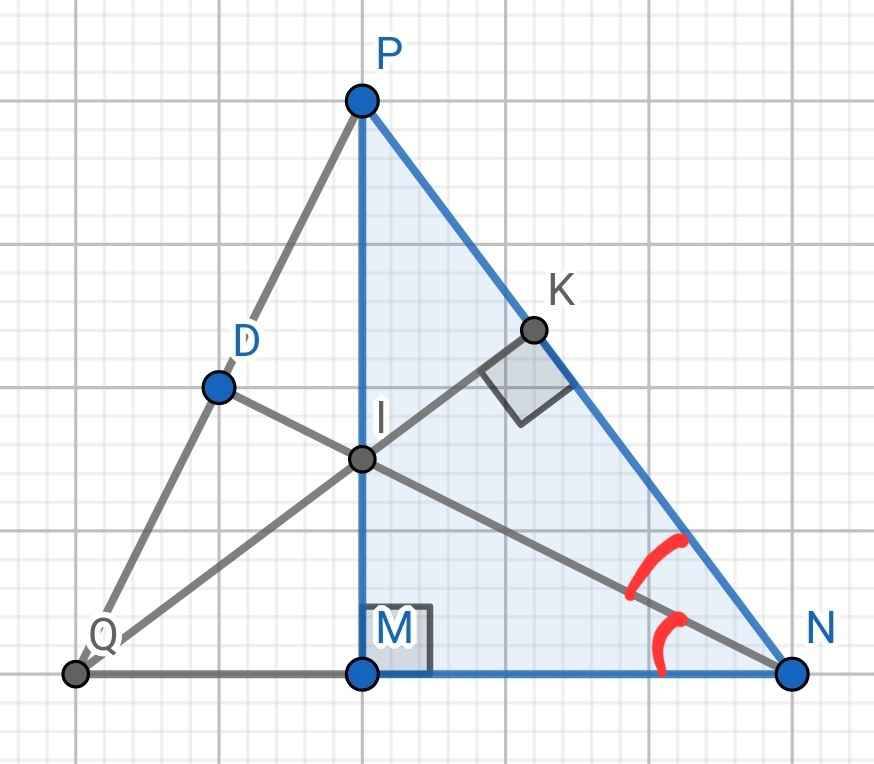
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
Đúng 2
Bình luận (1)