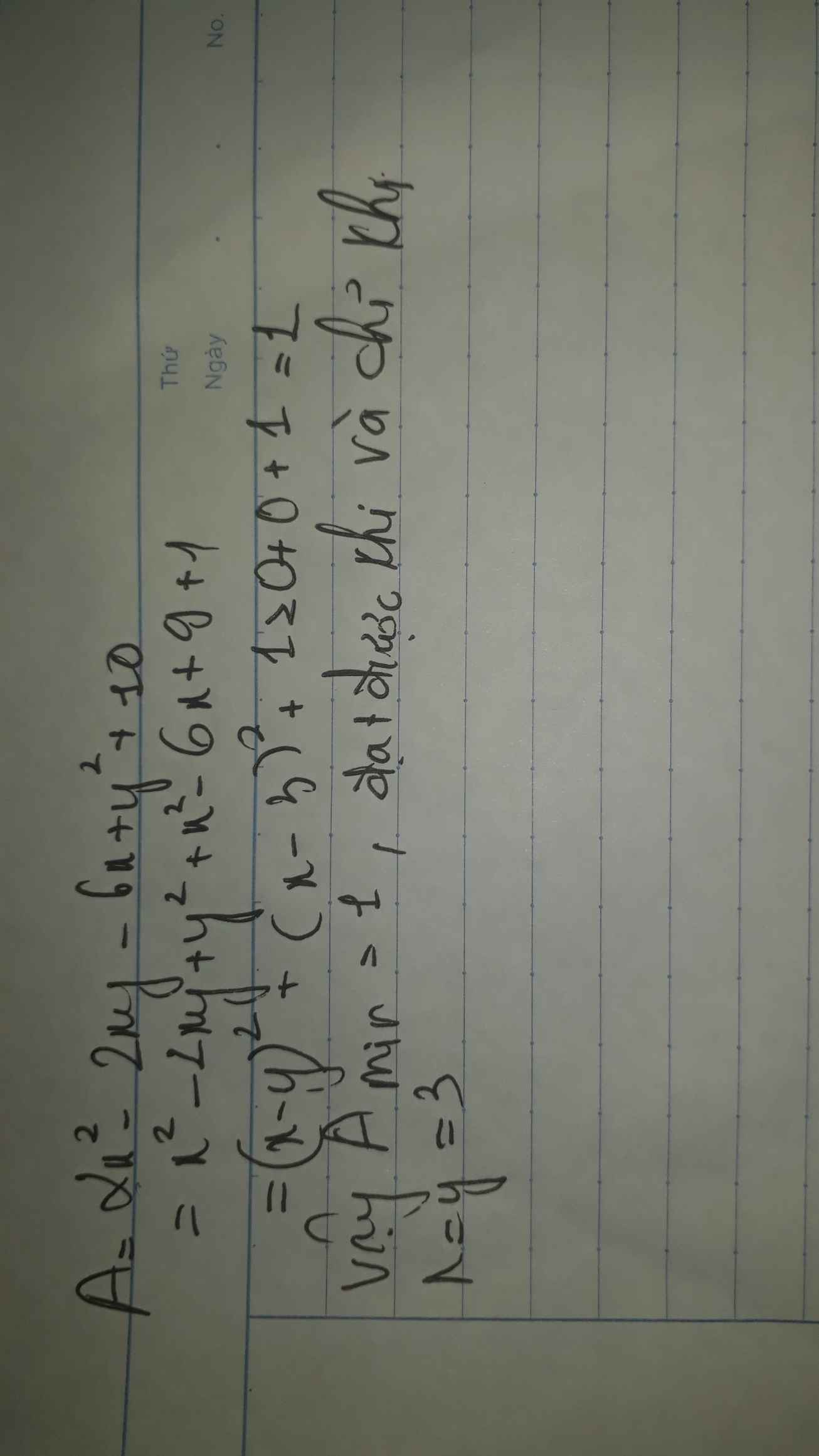tìm GTNN của biểu thức:P=5(2x2-2xy+y2)+2(y-3x+2)

Những câu hỏi liên quan
Tìm cặp số (x,y)(x,y) để P=5(2x2−2xy+y2)+2(y−3x+2)P=5(2x2−2xy+y2)+2(y−3x+2) đạt giá trị nhỏ nhất
tìm GTNN của biểu thức A=2x2-2xy-6x+y2+10
`A=2x^2-2xy-6x+y^2+10`
`A=x^2-2xy+y^2+x^2-6x+10`
`A=(x-y)^2+x^2-6x+9+1`
`A=(x-y)^2+(x-3)^2+1`
Vì `(x-y)^2+(x-3)^2>=0=>A>=1`
Dấu "=" xảy ra khi `{(x-y=0),(x-3=0):}<=>x=y=3`
Đúng 1
Bình luận (0)
A=\(\left(x^2-2xy+y^2\right)+\left(x^2-6x+9\right)+1=\left(x-y\right)^2+\left(x-3\right)^2+1\ge1\\ \)
dấu= xảy ra khi x=y=3
tick mik nha
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tính GTNN, GTLN của các biểu thức sau:
a)A(x,y)=4x2+y2+4x-y+1
b)B(x,y)=2x2+y2+2xy-x+5
Toán lớp 8Lớn nhất - nhỏ nhất
tìm giá trị nhỏ nhất của biểu thức:P=5(2x^2-2xy+y^2)+2(y-3x+2)
Tìm GTNN của các biểu thức sau
a) A= x(x-3)(x-4)(x-7)
b) B= 2x2+y2 - 2xy - 2x +3
c) C = x2 +y2 -3x +3y
Xét biểu thức \(A=x\left(x-3\right)\left(x-4\right)\left(x-7\right)=\left(x^2-7x\right)\left(x^2-7x+12\right)\)
Đặt \(x^2-7x+6\rightarrow t\)Khi đó \(A=\left(t-6\right)\left(t+6\right)=t^2-36\ge-36\)
Dấu "=" xảy ra khi và chỉ khi \(t=0\)hay \(x^2-7x+6=0=>\left(x-6\right)\left(x-1\right)=0=>\orbr{\begin{cases}x=6\\x=1\end{cases}}\)
Vậy GTNN của biểu thức \(A=-36\)đạt được khi \(x=6orx=1\)
Xét biểu thức \(B=2x^2+y^2-2xy-2x+3=\left(x^2-2xy+y^2\right)+x^2-2x+1+2\)
\(=\left(x-y\right)^2+\left(x-1\right)^2+2\ge2\)
Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-y=0\\x-1=0\end{cases}< =>\hept{\begin{cases}1-y=0\\x=1\end{cases}}< =>\hept{\begin{cases}x=1\\y=1\end{cases}< =>x=y=1}}\)
Vậy GTNN của biểu thức \(B=2\)đạt được khi \(x=y=1\)
Xét biểu thức \(C=x^2+y^2-3x+3y=\left(x^2-3x+\frac{9}{4}\right)+\left(y^2+3y+\frac{9}{4}\right)-\frac{9}{2}\)
\(=\left(x^2-3x+\frac{3^2}{2^2}\right)+\left(y^2+3y+\frac{3^2}{2^2}\right)-\frac{9}{2}=\left(x-\frac{3}{2}\right)^2+\left(y+\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-\frac{3}{2}=0\\y+\frac{3}{2}=0\end{cases}}< =>\hept{\begin{cases}x=\frac{3}{2}\\y=-\frac{3}{2}\end{cases}< =>x=-y=\frac{3}{2}}\)
Vậy GTNN của biểu thức \(C=-\frac{9}{2}\)đạt được khi \(x=-y=\frac{3}{2}\)
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
Đúng 1
Bình luận (0)
a) 3x(x+1)-x(3x+2)
b) 2x(x2-5x+6)+(x-1)(x+3)
c) (x2-xy+y2)-(x2+2xy+y2)
d) (2/5xy+x-y)-(3x+4y)-2/5xy
e) 2xy(x2-4xy+4y2)
f) (x+y)(xy+5)
g) (x3-2x2-x+2):(x-1)
h) (2x2+3x-2):(2x-1)
tìm x,y để biểu thức đạt GTNN và GTNN là bao nhiêu
L=y2 -2xy +3x2 +2y -14x +1949
1)Tìm GTNN của bt sau:
A=2x2+y2-2x+2xy+2y+3
2) Cho 3x+3y=2021. Tính gt bt sau một cách hợp lí: P=x3+2021xy+y3
\(A=2x^2+y^2-2x+2xy+2y+3=y^2+2y\left(x+1\right)+\left(x+1\right)^2+\left(x^2-4x+4\right)-2=\left(y+x+1\right)^2+\left(x-2\right)^2-2\ge-2\)
\(minA=-2\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)
Đúng 2
Bình luận (0)
\(P=x^3+2021xy+y^3\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+2021xy\)
\(=\left(\dfrac{2021}{3}\right)^3\)
\(=\dfrac{8254655261}{27}\)
Đúng 3
Bình luận (0)