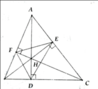
Cho tam giác ABC nhọn có các đường cao AD, BE, CF cắt nhau tại H.
a) Tính tổng \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}\)
b) Chứng minh: BH.BE + CH.CF = BC2
c) Chứng minh : H cách đều ba cạnh tam giác DEF
d) Trên các đoạn HB, HC lấy các điểm M, N tùy ý sao cho HM = CN
Chứng minh đường trung trực của đoạn MN luôn đi qua một điểm cố định