Bài 8: Vì em nhắn tin nhờ cô giảng bài 8 nên cô chỉ giảng bài 8 thôi nhé

Gọi các cạnh góc vuông, cạnh huyền của tam giác cần tìm lần lượt là: a; b; c

Theo bài ra ta có: a+b+c =36; \(\dfrac{a}{b}\) = \(\dfrac{3}{4}\)

\(\dfrac{a}{b}\) = \(\dfrac{3}{4}\) ⇒ \(\dfrac{a}{3}\) = \(\dfrac{b}{4}\) ⇒ \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{a^2+b^2}{9+16}\) (1)

Vì tam giác vuông nên ta theo pytago ta có: a² + b²  = c² (2)

Thay (2) vào (1) ta có: \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{c^2}{25}\)

⇒ \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) 

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) = \(\dfrac{a+b+c}{3+4+5}\) = \(\dfrac{36}{12}\) = 3

a = 3.3 = 9 (cm)

b = 3.4 = 12 (cm)

c = 3.5 = 15 (cm)

Kết luận: độ dài cạnh bé của góc vuông là: 9 cm

               dộ dài cạnh lớn của góc vuông là 12 cm

              độ dài cạnh huyền là 15 cm

Bài 9:

a,Gọi độ dài cạnh góc vuông là: a

Theo pytago ta có: a² + a² = 2² = 4 ⇒ 2a² = 4 ⇒ a² = 2 ⇒ a = \(\sqrt{2}\)

b, Gọi độ dài cạnh góc vuông là :b 

Theo pytago ta có:

b² + b² = 10² =100 ⇒ 2b² = 100 ⇒ b² = 50⇒ b = 5\(\sqrt{2}\)

Bài 8 cô làm rồi nhé. 

Bài 10 ; Gọi độ dài các cạnh góc của tam giác vuông lần lượt là:

a; b theo bài ra ta có: 

\(\dfrac{a}{5}\) = \(\dfrac{b}{12}\) \(\Rightarrow\) \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{a^2+b^2}{25+144}\) (1)

Theo pytago ta có: a² + b² = 52² = 2704 (2)

Thay (2) vào (1) ta có: \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{2704}{169}\) = 16

⇒ a² = 25.16 = (4.5)² ⇒ a = 20

b² = 144.16 = (12.4)² ⇒ b = 48

Bài 11 

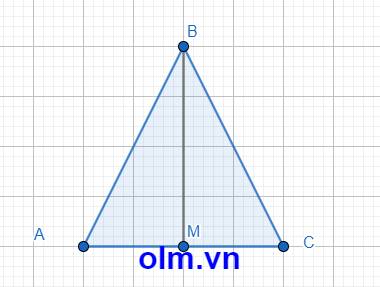
AM = \(\dfrac{1}{2}\) AC ( vì M là trung điểm AC)

AM = 16 \(\times\) \(\dfrac{1}{2}\) = 8 (cm)

BM \(\perp\)AC ( vì trong tam giác cân đường trung tuyến cũng là đường cao, đường trung trực)

⇒\(\Delta\)MAB vuông tại M

Xét tam giác vuông MAB theo pytago ta có:

AB² = AM² + BM²

⇒ BM² = AM² - AM²  = 17² - 8² = 225

    BM = \(\sqrt{225}\) cm = 15 cm

Kết luận BM = 15 cm

bài 66 trang 49 sách bài tập toán lớp 7

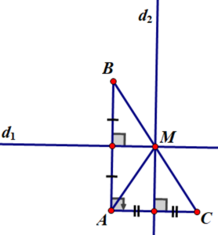
+ Giả sử ∆ABC vuông tại A.

d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.

d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.

+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.

+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)

+ M là trung điểm của cạnh BC (đpcm)

*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC

⇒ MB = MC = BC/2

Mà MA = MB = MC (cmt)

⇒ MA = BC/2

Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

ko biết làm giúp bạn này với

a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d₁, d₂

của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)

Vì MA = MB (M thuộc đường trung trực của AB)

MA = MC (M thuộc đường trung trực của AC)

=> MB = MC

Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC

b) M là trung điểm Bc => MB = BC

mà AM = MB nên MA = BC

Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d₁, d₂

của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)

Vì MA = MB (M thuộc đường trung trực của AB)

MA = MC (M thuộc đường trung trực của AC)

=> MB = MC

Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC

b) M là trung điểm Bc => MB = BC

mà AM = MB nên MA = BC

Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền

bạn Tham khảo bài bạn này 

a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d₁, d₂

của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)

Vì MA = MB (M thuộc đường trung trực của AB)

MA = MC (M thuộc đường trung trực của AC)

=> MB = MC

Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC

b) M là trung điểm Bc => MB =  BC

mà AM = MB nên MA = BC

Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

Bài 2: 

Gọi tam giác vuông đo là ΔABC vuông tại A có AH là đường cao 

Theo đề, ta có: \(\dfrac{AB}{AC}=\dfrac{3}{7}\)

\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{9}{49}\)

\(\Leftrightarrow HB=\dfrac{9}{49}HC\)

Ta có: \(HB\cdot HC=AH^2\)

\(\Leftrightarrow HC^2=42^2:\dfrac{9}{49}=9604\)

\(\Leftrightarrow HC=98\left(cm\right)\)

\(\Leftrightarrow HB=42cm\)

a,b,c là số đo các cạnh của tam giác nên là các số dương, dễ thấy x>y;z

nếu x;y;z là số đo các cạnh của 1 tam giác vuông khác thì x là cạnh huyền

ta xét x²=y²+z² <=> \(\left(9a+4b+8c\right)^2=\left(4a+b+4c\right)^2+\left(8a+4b+7c\right)^2\)

<=> 81a²+16b²+64c²+72ab+64bc+144ca=80a²+17b²+65c²+72ab+64bc+144ca

<=>a²=b²+c²(đúng do a;b;c là số đo 3 cạnh của 1 tam giác vuông với a độ dài là cạnh huyền,áp dụng định lý Pytago)

Ta đã chứng minh được : x²=y²+z² .Theo định lý Pytago đảo suy ra x;y;z cũng là số đo 3 cạnh của 1 tam giác vuông 

Ta có a,b,c là số đo các cạnh của tam giác nên là các số dương.

Ta thấy x>y;z
Nếu x;y;z là số đo các cạnh của 1 tam giác vuông khác thì x là cạnh huyền
Xét x^2=y^2+z^2 <=>( 9a + 4b + 8c)^2 = (4a + b + 4c)^2+ (8a + 4b + 7c)^2
<=> 81a^2+64c^2+72ab+64bc+144ca=80a^2+17b2^+65c^2+72ab+64bc+144ca
<=>a^2=b^2+c^2
 do a;b;c là số đo 3 cạnh của 1 tam giác vuông với a độ dài là cạnh huyền,

Áp dụng định lý Pytago.Ta chứng minh được :

x^2=y^2+z^2
=> x;y;z là số đo 3 cạnh của 1 tam giác vuông (Theo định lý Pytago đảo )

NHỚ TK MK NHALưu Đức Mạnh