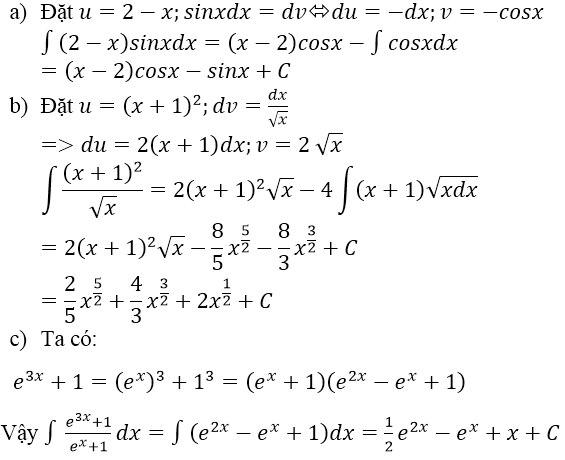\(I1=\int e^{\sqrt{x}}\sqrt{x}dx\)

Những câu hỏi liên quan
Tìm các nguyên hàm sau
1.intfrac{9x^2}{sqrt{1-x^3}}dx
2.intfrac{1}{sqrt{x}left(1+sqrt{x}right)^3}dx
3.intfrac{x}{sqrt{2x+3}}dx
4.int frac{e^{2x}}{sqrt{1+e^x}} dx
5.intfrac{sqrt[3]{1+lnx}}{x}dx
6.int cosxsin3xdx
7.int (x2+2x-1)exdx
8.int excosxdx
9.int xsin(2x+1)dx
10.int (1-2x)e3xdx
Đọc tiếp
Tìm các nguyên hàm sau
1.\(\int\frac{9x^2}{\sqrt{1-x^3}}dx\)
2.\(\int\frac{1}{\sqrt{x}\left(1+\sqrt{x}\right)^3}dx\)
3.\(\int\frac{x}{\sqrt{2x+3}}dx\)
4.\(\int\) \(\frac{e^{2x}}{\sqrt{1+e^x}}\) dx
5.\(\int\frac{\sqrt[3]{1+lnx}}{x}dx\)
6.\(\int\) cosxsin3xdx
7.\(\int\) (x2+2x-1)exdx
8.\(\int\) excosxdx
9.\(\int\) xsin(2x+1)dx
10.\(\int\) (1-2x)e3xdx
Không phải tất cả các câu đều dùng nguyên hàm từng phần được đâu nhé, 1 số câu phải dùng đổi biến, đặc biệt những câu liên quan đến căn thức thì đừng dại mà nguyên hàm từng phần (vì càng nguyên hàm từng phần biểu thức nó càng phình to ra chứ không thu gọn lại, vĩnh viễn không ra kết quả đâu)
a/ \(I=\int\frac{9x^2}{\sqrt{1-x^3}}dx\)
Đặt \(u=\sqrt{1-x^3}\Rightarrow u^2=1-x^3\Rightarrow2u.du=-3x^2dx\)
\(\Rightarrow9x^2dx=-6udu\)
\(\Rightarrow I=\int\frac{-6u.du}{u}=-6\int du=-6u+C=-6\sqrt{1-x^3}+C\)
b/ Đặt \(u=1+\sqrt{x}\Rightarrow du=\frac{dx}{2\sqrt{x}}\Rightarrow2du=\frac{dx}{\sqrt{x}}\)
\(\Rightarrow I=\int\frac{2du}{u^3}=2\int u^{-3}du=-u^{-2}+C=-\frac{1}{u^2}+C=-\frac{1}{\left(1+\sqrt{x}\right)^2}+C\)
c/ Đặt \(u=\sqrt{2x+3}\Rightarrow u^2=2x\Rightarrow\left\{{}\begin{matrix}x=\frac{u^2}{2}\\dx=u.du\end{matrix}\right.\)
\(\Rightarrow I=\int\frac{u^2.u.du}{2u}=\frac{1}{2}\int u^2du=\frac{1}{6}u^3+C=\frac{1}{6}\sqrt{\left(2x+3\right)^3}+C\)
d/ Đặt \(u=\sqrt{1+e^x}\Rightarrow u^2-1=e^x\Rightarrow2u.du=e^xdx\)
\(\Rightarrow I=\int\frac{\left(u^2-1\right).2u.du}{u}=2\int\left(u^2-1\right)du=\frac{2}{3}u^3-2u+C\)
\(=\frac{2}{3}\sqrt{\left(1+e^x\right)^2}-2\sqrt{1+e^x}+C\)
e/ Đặt \(u=\sqrt[3]{1+lnx}\Rightarrow u^3=1+lnx\Rightarrow3u^2du=\frac{dx}{x}\)
\(\Rightarrow I=\int u.3u^2du=3\int u^3du=\frac{3}{4}u^4+C=\frac{3}{4}\sqrt[3]{\left(1+lnx\right)^4}+C\)
f/ \(I=\int cosx.sin^3xdx\)
Đặt \(u=sinx\Rightarrow du=cosxdx\)
\(\Rightarrow I=\int u^3du=\frac{1}{4}u^4+C=\frac{1}{4}sin^4x+C\)
Từ phần này trở đi mới bắt đầu xài nguyên hàm từng phần:
g/ \(I=\int\left(x^2+2x-1\right)e^xdx\)
Đặt \(\left\{{}\begin{matrix}u=x^2+2x-1\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\left(2x+2\right)dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=\left(x^2+2x-1\right)e^x-\int\left(2x+2\right)e^xdx\)
Xét \(J=\int\left(2x+2\right)e^xdx\)
Đặt \(\left\{{}\begin{matrix}u=2x+2\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow J=\left(2x+2\right)e^x-\int2e^xdx=\left(2x+2\right)e^x-2e^x+C=2x.e^x+C\)
\(\Rightarrow I=\left(x^2+2x-1\right)e^x-2x.e^x+C=\left(x^2-1\right)e^x+C\)
Xem thêm câu trả lời
1)intsqrt{frac{1-sqrt{x}}{1+sqrt{x}}}dx
2)intfrac{dx}{left(e^x+1right)left(x^2+1right)}
3)intfrac{1+2xsqrt{1-x^2}+2x^2}{1+x+sqrt{1+x^2}}dx
4)intfrac{sin^6x+ctext{os}^6x}{1+6^x}dx
5)int_0^{frac{pi}{2}}frac{sqrt{ctext{os}x}}{sqrt{stext{inx}}+sqrt{ctext{os}x}}dx
6)intfrac{x^4}{2^x+1}dx
7)int_0^{frac{pi^2}{4}}sinsqrt{x}dx
8)intsqrt[6]{1-ctext{os}^3x}.stext{inx}.ctext{os}^5xdx
9)intsqrt{frac{1}{4x}+frac{sqrt{x}+e^x}{sqrt{x}.e^x}}dx
10)intfrac{ctext{os}x+stext{inx}}{left(e^xstext{inx}+1right)...
Đọc tiếp
1)\(\int\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}dx\)
2)\(\int\frac{dx}{\left(e^x+1\right)\left(x^2+1\right)}\)
3)\(\int\frac{1+2x\sqrt{1-x^2}+2x^2}{1+x+\sqrt{1+x^2}}\)dx
4)\(\int\frac{sin^6x+c\text{os}^6x}{1+6^x}dx\)
5)\(\int_0^{\frac{\pi}{2}}\frac{\sqrt{c\text{os}x}}{\sqrt{s\text{inx}}+\sqrt{c\text{os}x}}dx\)
6)\(\int\frac{x^4}{2^x+1}dx\)
7)\(\int_0^{\frac{\pi^2}{4}}sin\sqrt{x}dx\)
8)\(\int\sqrt[6]{1-c\text{os}^3x}.s\text{inx}.c\text{os}^5xdx\)
9)\(\int\sqrt{\frac{1}{4x}+\frac{\sqrt{x}+e^x}{\sqrt{x}.e^x}}dx\)
10)\(\int\frac{c\text{os}x+s\text{inx}}{\left(e^xs\text{inx}+1\right)s\text{inx}}dx\)
Tính nguyên hàm của:1, intdfrac{x^3}{x-2}dx2, intdfrac{dx}{xsqrt{x^2+1}}3, int(dfrac{5}{x}+sqrt{x^3})dx4, intdfrac{xsqrt{x}+sqrt{x}}{x^2}dx5, intdfrac{dx}{sqrt{1-x^2}}
Đọc tiếp
Tính nguyên hàm của:
1, \(\int\)\(\dfrac{x^3}{x-2}dx\)
2, \(\int\)\(\dfrac{dx}{x\sqrt{x^2+1}}\)
3, \(\int\)\((\dfrac{5}{x}+\sqrt{x^3})dx\)
4, \(\int\)\(\dfrac{x\sqrt{x}+\sqrt{x}}{x^2}dx\)
5, \(\int\)\(\dfrac{dx}{\sqrt{1-x^2}}\)
a. \(\int\dfrac{x^3}{x-2}dx=\int\left(x^2+2x+4+\dfrac{8}{x-2}\right)dx=\dfrac{1}{3}x^3+x^2+4x+8ln\left|x-2\right|+C\)
b. \(\int\dfrac{dx}{x\sqrt{x^2+1}}=\int\dfrac{xdx}{x^2\sqrt{x^2+1}}\)
Đặt \(\sqrt{x^2+1}=u\Rightarrow x^2=u^2-1\Rightarrow xdx=udu\)
\(I=\int\dfrac{udu}{\left(u^2-1\right)u}=\int\dfrac{du}{u^2-1}=\dfrac{1}{2}\int\left(\dfrac{1}{u-1}-\dfrac{1}{u+1}\right)du=\dfrac{1}{2}ln\left|\dfrac{u-1}{u+1}\right|+C\)
\(=\dfrac{1}{2}ln\left|\dfrac{\sqrt{x^2+1}-1}{\sqrt{x^2+1}+1}\right|+C\)
c. \(\int\left(\dfrac{5}{x}+\sqrt{x^3}\right)dx=\int\left(\dfrac{5}{x}+x^{\dfrac{3}{2}}\right)dx=5ln\left|x\right|+\dfrac{2}{5}\sqrt{x^5}+C\)
d. \(\int\dfrac{x\sqrt{x}+\sqrt{x}}{x^2}dx=\int\left(x^{-\dfrac{1}{2}}+x^{-\dfrac{3}{2}}\right)dx=2\sqrt{x}-\dfrac{1}{2\sqrt{x}}+C\)
e. \(\int\dfrac{dx}{\sqrt{1-x^2}}=arcsin\left(x\right)+C\)
Đúng 1
Bình luận (1)
Tính các nguyên hàm sau :
a) intleft(2x-3right)sqrt{x-3}dx, đặt usqrt{x-3}
b) intdfrac{x}{left(1+x^2right)^{dfrac{3}{2}}}dx , đặt usqrt{x^2+1}
c) intdfrac{e^x}{e^x+e^{-x}}dx, đặt ue^{2x}+1
d) intdfrac{1}{sin x-sin a}dx
e) intsqrt{x}sinsqrt{x}dx, đặt tsqrt{x}
g) int xlndfrac{x}{1+x}dx
Đọc tiếp
Tính các nguyên hàm sau :
a) \(\int\left(2x-3\right)\sqrt{x-3}dx\), đặt \(u=\sqrt{x-3}\)
b) \(\int\dfrac{x}{\left(1+x^2\right)^{\dfrac{3}{2}}}dx\) , đặt \(u=\sqrt{x^2+1}\)
c) \(\int\dfrac{e^x}{e^x+e^{-x}}dx\), đặt \(u=e^{2x}+1\)
d) \(\int\dfrac{1}{\sin x-\sin a}dx\)
e) \(\int\sqrt{x}\sin\sqrt{x}dx,\) đặt \(t=\sqrt{x}\)
g) \(\int x\ln\dfrac{x}{1+x}dx\)
a)
Đặt \(u=\sqrt{x-3}\Rightarrow x=u^2+3\)
\(I_1=\int (2x-3)\sqrt{x-3}dx=\int (2u^2+3)ud(u^2+3)=2\int (2u^2+3)u^2du\)
\(\Leftrightarrow I_1=4\int u^4du+6\int u^2du=\frac{4u^5}{5}+2u^3+c\)
b)
\(I_2=\int \frac{xdx}{\sqrt{(x^2+1)^3}}=\frac{1}{2}\int \frac{d(x^2+1)}{\sqrt{(x^2+1)^2}}\)
Đặt \(u=\sqrt{x^2+1}\). Khi đó:
\(I_2=\frac{1}{2}\int \frac{d(u^2)}{u^3}=\int \frac{udu}{u^3}=\int \frac{du}{u^2}=\frac{-1}{u}+c\)
c)
\(I_3=\int \frac{e^xdx}{e^x+e^{-x}}=\int \frac{e^{2x}dx}{e^{2x}+1}=\frac{1}{2}\int\frac{d(e^{2x}+1)}{e^{2x}+1}\)
\(\Leftrightarrow I_3=\frac{1}{3}\ln |e^{2x}+1|+c=\frac{1}{2}\ln|u|+c\)
Đúng 0
Bình luận (0)
d)
\(I_4=\int \frac{dx}{\sin x-\sin a}=\int \frac{dx}{2\cos \left ( \frac{x+a}{2} \right )\sin \left ( \frac{x-a}{2} \right )}\)
\(\Leftrightarrow I_4=\frac{1}{\cos a}\int \frac{\cos \left ( \frac{x+a}{2}-\frac{x-a}{2} \right )dx}{2\cos \left ( \frac{x+a}{2} \right )\sin \left ( \frac{x-a}{2} \right )}=\frac{1}{\cos a}\int \frac{\cos \left ( \frac{x-a}{2} \right )dx}{2\sin \left ( \frac{x-a}{2} \right )}+\frac{1}{\cos a}\int \frac{\sin \left ( \frac{x+a}{2} \right )dx}{2\cos \left ( \frac{x+a}{2} \right )}\)
\(\Leftrightarrow I_4=\frac{1}{\cos a}\left ( \ln |\sin \frac{x-a}{2}|-\ln |\cos \frac{x+a}{2}| \right )+c\)
e)
Đặt \(t=\sqrt{x}\Rightarrow x=t^2\)
\(I_5=\int t\sin td(t^2)=2\int t^2\sin tdt\)
Đặt \(\left\{\begin{matrix} u=t^2\\ dv=\sin tdt\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=2tdt\\ v=-\cos t\end{matrix}\right.\)
\(\Rightarrow I_5=-2t^2\cos t+4\int t\cos tdt\)
Tiếp tục nguyên hàm từng phần \(\Rightarrow \int t\cos tdt=t\sin t+\cos t+c\)
\(\Rightarrow I_5=-2t^2\cos t+4t\sin t+4\cos t+c\)
Đúng 0
Bình luận (0)
g)
Có \(I_6=\int x\ln \left ( \frac{x}{x+1} \right )dx=\int x\ln xdx-\int x\ln (x+1)dx\)
Đặt \(\left\{\begin{matrix} u=\ln x\\ dv=xdx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dx}{x}\\ v=\frac{x^2}{2}\end{matrix}\right.\Rightarrow \int x\ln xdx=\frac{x^2\ln x}{2}-\int \frac{xdx}{2}\)
\(\Leftrightarrow \int x\ln xdx=\frac{x^2\ln x}{2}-\frac{x^2}{4}+c\)
Tương tự, \(\int x\ln (x+1)dx=\frac{x^2\ln (x+1)}{2}-\int \frac{x^2}{2(x+1)}dx\)
\(=\frac{x^2\ln (x+1)}{2}-\frac{x^2}{4}+\frac{x}{2}-\frac{\ln (x+1)}{2}+c\)
Suy ra \(I_5=\frac{x^2}{2}\ln \frac{x}{x+1}+\frac{1}{2}\ln|x+1|-\frac{x}{2}+c\)
Đúng 0
Bình luận (0)
\(\int\sqrt{e^x-1}dx\)
\(\int\frac{\sqrt{1+x^2}}{x^4}dx\)
Câu 1:Gọi biểu thức là $A$. Đặt \(\sqrt{e^x-1}=t\)
\(\Rightarrow e^x=t^2+1\Rightarrow d(e^x)=d(t^2+1)=2tdt=e^xdx=(t^2+1)dx\)
\(\Rightarrow \int \frac{2t^2}{t^2+1}dt=\int \left (2-\frac{2}{t^2+1} \right)dt\)
Đặt \(t=\tan m\Rightarrow dt=\frac{dm}{\cos^2 m}\Rightarrow \int \frac{2dt}{t^2+1}=\int 2dm=2m\)
\(\Rightarrow A=2t-2m+c=2\sqrt{e^x-1}-2\tan ^{-1} (\sqrt{e^x-1})+c\)
Câu 2: Đặt \(x=\tan t\Rightarrow dx=\frac{dt}{\cos^2 t}, x^2+1=\frac{1}{\cos^2 t}\) với \(\frac{-\pi}{2} < t< \frac{\pi}{2}\)
Gọi biểu thức là $B$. Ta có
\(B=\int \frac{\cos t dt}{\sin ^4t}=\int \frac{d(\sin t)}{\sin^4 t}=\frac{-\sin ^{-3} t}{3}+c\) \(=-\frac{\sqrt{(x^2+1)^3}}{3x^3}+c\)
Đúng 0
Bình luận (0)
Tính :
a) intleft(2-xright)sin xdx
b) intdfrac{left(x+1right)^2}{sqrt{x}}dx
c) intdfrac{3^{3x}+1}{e^x+1}dx
d) intdfrac{1}{left(sin x+cos xright)^2}dx
e) intdfrac{1}{sqrt{1+x}+sqrt{x}}dx
g) intdfrac{1}{left(1+xright)left(2-xright)}dx
Đọc tiếp
Tính :
a) \(\int\left(2-x\right)\sin xdx\)
b) \(\int\dfrac{\left(x+1\right)^2}{\sqrt{x}}dx\)
c) \(\int\dfrac{3^{3x}+1}{e^x+1}dx\)
d) \(\int\dfrac{1}{\left(\sin x+\cos x\right)^2}dx\)
e) \(\int\dfrac{1}{\sqrt{1+x}+\sqrt{x}}dx\)
g) \(\int\dfrac{1}{\left(1+x\right)\left(2-x\right)}dx\)
Mọi người ơi , giúp e tính tích phân bất định với ạ ! Cảm ơn m.n ạ !
a.intfrac{x+6}{sqrt{x^2-2x+10}}dx
b.intfrac{x}{sqrt{3-2x-x^2}}dx
c.intsqrt{frac{1-sqrt{x}}{1+sqrt{x}}}dx
d,intfrac{dx}{1+tanx}
e.int tan^3xdx
f. int cos^3xdx
g. int sin^2x.cos^3xdx
h. int sinx.cos2xdx
i. intfrac{sin2x}{1+cos^2x}dx
Đọc tiếp
Mọi người ơi , giúp e tính tích phân bất định với ạ ! Cảm ơn m.n ạ !
a.\(\int\frac{x+6}{\sqrt{x^2-2x+10}}dx\)
b.\(\int\frac{x}{\sqrt{3-2x-x^2}}dx\)
c.\(\int\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}dx\)
d,\(\int\frac{dx}{1+tanx}\)
e.\(\int tan^3xdx\)
f. \(\int cos^3xdx\)
g. \(\int sin^2x.cos^3xdx\)
h. \(\int sinx.cos2xdx\)
i. \(\int\frac{sin2x}{1+cos^2x}dx\)
a.
\(I=\int\frac{\frac{1}{2}\left(2x-2\right)+7}{\sqrt{x^2-2x+10}}dx=\frac{1}{2}\int\frac{2x-2}{\sqrt{x^2-2x+10}}dx+7\int\frac{1}{\sqrt{x^2-2x+10}}dx=\frac{1}{2}I_1+7I_2\)
Xét \(I_1=\int\frac{2x-2}{\sqrt{x^2-2x+10}}dx=\int\frac{d\left(x^2-2x+10\right)}{\sqrt{x^2-2x+10}}=2\sqrt{x^2-2x+10}+C_1\)
Xét \(I_2=\int\frac{dx}{\sqrt{x^2-2x+10}}=\int\frac{dx}{\sqrt{\left(x-1\right)^2+9}}\)
Đặt
\(u=x-1+\sqrt{\left(x-1\right)^2+10}\Rightarrow du=\left(1+\frac{\left(x-1\right)}{\sqrt{\left(x-1\right)^2+10}}\right)dx=\frac{x-1+\sqrt{\left(x-1\right)^2+10}}{\sqrt{\left(x-1\right)^2+10}}dx\)
\(\Rightarrow du=\frac{u}{\sqrt{\left(x-1\right)^2+10}}dx\Rightarrow\frac{dx}{\sqrt{\left(x-1\right)^2+10}}=\frac{du}{u}\)
\(\Rightarrow I_2=\int\frac{du}{u}=ln\left|u\right|+C_2=ln\left|x-1+\sqrt{x^2-2x+10}\right|+C_2\)
\(\Rightarrow I=\sqrt{x^2-2x+10}+7ln\left|x-1+\sqrt{x^2-2x+10}\right|+C\)
Đúng 0
Bình luận (0)
2.
\(I=\int\frac{\frac{1}{2}\left(2x+2\right)-1}{\sqrt{3-2x-x^2}}dx=\frac{1}{2}\int\frac{2x+2}{\sqrt{3-2x-x^2}}dx-\int\frac{1}{\sqrt{3-2x-x^2}}dx=\frac{1}{2}I_1-I_2\)
Xét \(I_1=\int\frac{2x+2}{\sqrt{3-2x-x^2}}dx=-\int\frac{d\left(3-2x-x^2\right)}{\sqrt{3-2x-x^2}}=-2\sqrt{3-2x-x^2}+C_1\)
Xét \(I_2=\int\frac{1}{\sqrt{3-2x-x^2}}dx=\int\frac{1}{\sqrt{4-\left(x+1\right)^2}}dx\)
Đặt \(x+1=2sinu\Rightarrow dx=2cosu.du\)
\(\Rightarrow I_2=\int\frac{2cosu.du}{2.cosu}=\int du=u+C_2=arcsin\left(\frac{x+1}{2}\right)+C_2\)
\(\Rightarrow I=-\sqrt{3-2x-x^2}-arcsin\left(\frac{x+1}{2}\right)+C\)
Đúng 0
Bình luận (0)
c/
\(I=\int\frac{1-\sqrt{x}}{\sqrt{1-x}}dx\)
Đặt \(\sqrt{x}=sint\Rightarrow x=sin^2t\Rightarrow dx=2sint.cost.dt\)
\(\Rightarrow I=\int\frac{2sint.cost\left(1-sint\right)}{\sqrt{1-sin^2t}}dt=\int\frac{2sint.cost\left(1-sint\right)}{cost}dt=\int\left(2sint-2sin^2t\right)dt\)
\(=\int\left(2sint+cos2t-1\right)dt=-2cost+\frac{1}{2}sin2t-t+C\)
\(=-2\sqrt{1-sin^2t}+\frac{1}{2}sint\sqrt{1-sin^2t}-t+C\)
\(=-2\sqrt{1-x}+\frac{1}{2}\sqrt{x\left(1-x\right)}-arcsin\left(\sqrt{x}\right)+C\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm các nguyên hàm sau :
a) \(I_1=\int\frac{\sqrt{1+\ln x}}{x}dx\)
b) \(I_2=\int\frac{e^{2x}}{\sqrt[4]{e^x+1}}dx\)
c) \(I_3=\int x^2e^{x^3+6}dx\)
a) Đặt \(1+\ln x=t\) khi đó \(\frac{dx}{x}=dt\) và do đó
\(I_1=\int\sqrt{t}dt=\frac{2}{3}t^{\frac{3}{2}}+C=\frac{2}{3}\sqrt{\left(1+\ln x\right)^3}+C\)
b) Đặt \(\sqrt[4]{e^x+1}=t\) khi đó \(e^x+1=t^4\Rightarrow e^x=t^4-1\) và \(e^xdx=4t^3dt\) , \(e^{2x}dx=e^x.e^xdx=\left(t^4-1\right)4t^3dt\)
Do đó :
\(I_2=4\int\frac{t^3\left(t^4-1\right)}{t}dt=4\int\left(t^6-t^2\right)dt=4\left[\frac{t^7}{7}-\frac{t^3}{3}\right]+C\)
\(=4\left[\frac{1}{7}\sqrt[4]{\left(e^x+1\right)^7}-\frac{1}{3}\sqrt[4]{\left(e^x+1\right)^3}\right]+C\)
c) Lưu ý rằng \(x^2dx=\frac{1}{3}d\left(x^3+C\right)\) do đó :
\(I_3=\int x^2e^{x^{3+6}dx}=\frac{1}{3}\int e^{x^{3+6}}d\left(x^3+6\right)=\frac{1}{3}e^{x^{3+6}}+C\)
Đúng 0
Bình luận (0)
1.\(\int_0^{\dfrac{\pi}{4}}\dfrac{\sin2x}{\sqrt{1+\cos^4x}}dx\)
2.\(\int_0^{ln3}\dfrac{e^x}{\sqrt{e^x+1}+1}dx\)
3.\(\int_1^2\dfrac{3x+1}{\sqrt{x^2+3x+9}}dx\)
4.\(\int\limits^{\dfrac{\pi}{3}}_{-\dfrac{\pi}{3}}\sin x\sqrt{3+\cos^6x}dx\)