cho tam giác ABC vuông ở A và M là trung điểm của BC . Từ M kẻ MH vuông góc AB ( H thuộc AB) và MK vuông góc AC (K thuộc AC)
chứng minh:
a) AHMK là nhình chữ nhật
b) BHKM là hình bình hành
cho tam giác ABC vuông tại A và M là trung điểm BC. từ M kẻ MH vuông góc AB ( H thuộc AB) và MK vuông góc AC ( K thuộc AC) ; a) chứng minh: AHMK là hình chữ nhật; b) chứng minh:BHKM là hình bình hành;c) gọi E trung điểm của MH. chứng minh:B,E,K thẳng hàng
dạ cô vẽ dùng em hình
a, xét tứ giác AHMK có
góc MHA=90 độ( MH ⊥ Ab-gt)
góc MKA=90 độ( MK⊥ AC-gt)
góc HAK= 90 độ ( tam giác ABC vuông tại A-gt)
-> AHMK là hcn ( tứ giác có 3 góc vuông là hcn)2). Có : MH vuông góc với AB ( gt )
AC vuông góc với AB (
Δ
ABC vuông tại A)
=> MH//AC
Xét tam giác ABc có
MH//AC( cmt)
M là trung điểm BC (gt)
=> H là trung điểm AB (định lý đường trung bình của tam giác)(đpcm)
. Có: MK vuông góc AC ( gt)
AB vuông góc AC( tam giác ABC vuông tại A )
=> MK//AB
Có:MK//AB(cmt)
M là trung điểm BC ( gt)
=> K là trung điểm AC ( định lý đường trung bình của tam giác )
Có : H là trung điểm AB ( cmt)
=. BH=1/2AB
Xét tam giác ABC có
M là trung điểm BC(cmt)
K là trung điểm AC ( cmt)
=> MK là đưởng trung bình của tam giác ABC( dấu hiệu nhận biết)
=> MK=1/2AB
( tính chất đường trung bình của tam giác)
=> MK//AB(tính chất đường trung bình của tam giác) hay MK//BH
Có MK=1/2AB
BH= 1/2AB
=> MK=BH
Mà MK//BH(cmt)
=> BMKH là hình bình hành
VÌ BMKH là hình bình hành (cmt)
=> Hai đường chéo HM và BK cắt nhau tại trung điểm mỗi đường
Mà E là trung điểm HM ( gt)
=> E là trung điểm BK hay ba điểm B; E; K thẳng hàng(dpcm)
mình tự làm ne chắc do mạng mình bị lỗi bắm nhầm phải
Cho tam giác ABC vuông tại A , đường trung tuyến AM . Kẻ MH vuông góc với AB ( H thuộc AB ) , MK vuông góc với AC ( K thuộc AC )
a) Chứng minh : Tứ giác AKMH là hình chữ nhật
b) E là trung điểm của MH . Chứng minh tứ giác BHKM là hình bình hành
c ) Chứng minh 3 điểm B,E,K thẳng hàng
d) Gọi F là trung điểm của MK . Đường thảng HK cắt AE tại I và À tại J . Chứng minh HI = KJ
Bn tự vẽ hình nha
a, xét tứ giác AHMK có
góc MHA=90 độ( MH ⊥ Ab-gt)
góc MKA=90 độ( MK⊥ AC-gt)
góc HAK= 90 độ ( tam giác ABC vuông tại A-gt)
-> AHMK là hcn ( tứ giác có 3 góc vuông là hcn)
Tớ chỉ lm đc câu a thui nếu đúng like cho tớ nha![]()
b)AKMH là hình chữ nhật\(\Rightarrow\)EMK=90độ.
xét 2 \(\Delta\)vuông \(\Delta\)BHE và \(\Delta\)KME
có:HE=EM(1)\(\)
BEH=MEK(2 góc đối đỉnh)(2)
từ (1),(2)\(\Rightarrow\)\(\Delta\)BHE=\(\Delta\)KME(cgv-gn)
\(\Rightarrow\)BE=EK(2 cạnh t/ứ)
xét t/g BHKM có:EH=EM(3)
BE=EK(cmt)(4)
từ(3),(4)\(\Rightarrow\)BHKM là hình bình hành
a, xét tứ giác AHMK có
góc MHA=90 độ( MH ⊥ Ab-gt)
góc MKA=90 độ( MK⊥ AC-gt)
góc HAK= 90 độ ( tam giác ABC vuông tại A-gt)
-> AHMK là hcn ( tứ giác có 3 góc vuông là hcn)2). Có : MH vuông góc với AB ( gt )
AC vuông góc với AB (
Δ
ABC vuông tại A)
=> MH//AC
Xét tam giác ABc có
MH//AC( cmt)
M là trung điểm BC (gt)
=> H là trung điểm AB (định lý đường trung bình của tam giác)(đpcm)
. Có: MK vuông góc AC ( gt)
AB vuông góc AC( tam giác ABC vuông tại A )
=> MK//AB
Có:MK//AB(cmt)
M là trung điểm BC ( gt)
=> K là trung điểm AC ( định lý đường trung bình của tam giác )
Có : H là trung điểm AB ( cmt)
=. BH=1/2AB
Xét tam giác ABC có
M là trung điểm BC(cmt)
K là trung điểm AC ( cmt)
=> MK là đưởng trung bình của tam giác ABC( dấu hiệu nhận biết)
=> MK=1/2AB
( tính chất đường trung bình của tam giác)
=> MK//AB(tính chất đường trung bình của tam giác) hay MK//BH
Có MK=1/2AB
BH= 1/2AB
=> MK=BH
Mà MK//BH(cmt)
=> BMKH là hình bình hành
Xin lỗi nha. Mik chỉ biết làm câu a,b thôi à . Bạn tự vẽ hình nha
bài 7. cho tam giác abc vuông tại a . gọi m là trung điểm của bc . từ m kẻ mh vuông góc ab (h thuộc ab) mk vuông góc ac (k thuộc ac)
a) chứng minh tứ giác bhkm là hình bình hành.
b) chứng minh tứ giác hmck là hình bình hành.
c) chứng minh h là trung điểm của ab .
d) chứng minh bc=2hk
Bài 8. Cho hình bình hành ABCD, có 2 đường chéo AC, BD cắt nhau tại O. Đường thẳng bất kì qua O cắt AB, CD lần lượt ở M và N.
a) Chứng minh OM =ON
b) Tứ giác AMCN là hình gì? Vì sao?
c) Chứng minh BN // DM và BN = DM
Bài 9. Cho hình bình hành ABCD . Trên đường chéo BD lấy hai điểm M và N sao cho: BN=DN=1/3BD
a) Chứng minh :tam giác AMB=tam giác CND
b)Chứng minh rằng tứ giác AMCN là hình bình hành.
c) Gọi O là giao điểm của AC và BD , I là giao điểm của AM và BC . Chứng minh rằng: AM=2MI
d) Gọi K là giao điểm của CN và AD. Chứng minh I và K đối xứng với nhau qua O .
cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ MH, MK lần lượt vuông góc với AB và AC ( H thuộc AB và K thuộc AC)
a) chứng minh tứ giác AHKM là hình chữ nhật và AM = HK
b) chứng minh tứ giác BHKM là hình bình hành
c) gọi E là trung điểm của MH, F là trung điểm của MK. Đường thẳng HK cắt AE, À lần lượt tại I và D. Chứng minh HI = KD
Vẽ cả hình
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{HAK}=90^0\)
=>AHMK là hình chữ nhật
=>AM=HK
b: Xét ΔABC có
M là trung điểm của BC
MK//AB
Do đó: K là trung điểm của AC
Xét ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
Xét ΔABC có
M,K lần lượt là trung điểm của CB,CA
=>MK là đường trung bình của ΔABC
=>MK//AB và \(MK=\dfrac{AB}{2}\)
Ta có: MK//AB
H\(\in\)AB
Do đó: MK//HB
Ta có: \(MK=\dfrac{AB}{2}\)
\(AH=HB=\dfrac{AB}{2}\)
Do đó: MK=AH=HB
Xét tứ giác BHKM có
BH//KM
BH=KM
Do đó: BHKM là hình bình hành
c: Gọi O là giao điểm của AM và KH
Ta có: AHMK là hình chữ nhật
=>AM cắt KH tại trung điểm của mỗi đường
=>O là trung điểm của AM và KH
=>\(OA=OM=\dfrac{AM}{2};OK=OH=\dfrac{KH}{2}\)
mà AM=KH
nên OA=OM=OK=OH(1)
Xét ΔAKM có
AF,KO là các đường trung tuyến
AF cắt KO tại D
Do đó: D là trọng tâm của ΔAKM
Xét ΔAKM có
D là trọng tâm
KO là đường trung tuyến
Do đó: \(KD=\dfrac{2}{3}KO\left(2\right)\)
Xét ΔHAM có
AE,HO là các đường trung tuyến
AE cắt HO tại I
Do đó: I là trọng tâm của ΔHAM
Xét ΔHAM có
HO là đường trung tuyến
I là trọng tâm
Do đó: \(HI=\dfrac{2}{3}HO\left(3\right)\)
Từ (1),(2),(3) suy ra HI=KD
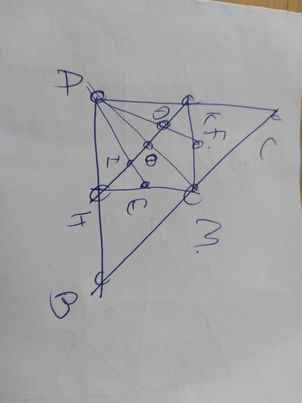
3. Cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ MH,MK lần lượt vuông góc với AB và AC (H thuộc AB và K thuộc AC).
a. Chứng minh tứ giác AKMH là hình chữ nhật.
b. Chứng minh tứ giác BHKM là hình bình hành.
c. Gọi E là trung điểm của MH, gọi F là trung điểm của MK. Đường thẳng HK cắt AE,AF lần lượt tại I và J. Chứng minh HI = KJ.
d. Gọi G là trọng tâm tam giác ABC. Giả sử tam giác ABG vuông tại G và AB = 4 √ 3 (cm). Tính độ dài EF.
4. Cho tam giác ABC vuông tại A , đường cao AH . Gọi D là điểm đối xứng với H qua AB,Elà điểm đối xứng với H qua AC . Gọi I là giao điểm của AB và DH, K là giao điểm của AC và EH .
a. Tứ giác AIHK là hình gì? Vì sao?
b. Chứng minh ba điểm D,E,A thẳng hàng.
c. Gọi M là trung điểm của BC. Chứng minh AM vuông góc IK.
a: Xét tứ giác AKMH có
\(\widehat{AKM}=\widehat{AHM}=\widehat{HAK}=90^0\)
Do đó: AKMH là hình chữ nhật
1: Xét tứ giác AHMK có
góc AHM=góc AKM=góc HAK=90 độ
=>AHMK là hình chữ nhật
2:
a: Xét ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
b: Xét ΔABC có
M là trung điểm của CB
MK//AB
Do đó: K là trung điểm của AC
Xét ΔABC có MK//AB
nên MK/AB=CM/CB=1/2
=>MK=1/2AB=HB
Xét tứ giác BHKM có
BH//KM
BH=KM
Do đó: BHKM là hình bình hành
=>BK cắt HM tại trung điểm của mỗi đường
=>B,E,K thẳng hàng
3:
a: Xét tứ giác ABMD có
AB//DM
AD//BM
Do đó: ABMD là hình bình hành
=>AD=MB=AM
b: Xét tứ giác AMCD có
AM//CD
AM=CD
AD=AM
Do đó: AMCD là hình thoi
Cho tam giác ABC vuông tại A, M là điểm nằm trên cạnh BC. Kẻ MH vuông góc với AB(H thuộc AB). MK vuông góc với AC( K thuộc AC)
a) CM Tứ giác AHMK là hình chữ nhật
b) Chứng minh MH/AC+MK/AB=1( MÌNH CẦN GIẢI GẤP CÂU B)
CÓ AI BIẾT CHỈ MÌNH NHÉ. CẢM ƠN CÁC BẠN NHIỀU
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó; AHMK là hình chữ nhật
cho tam giác abc vuông tại a (AB<AC) Gọi M là trung điểm của cạnh BC. Qua M vẽ MH vuông vs AB tại H và MK vuông góc vs AC tại K
a) Chứng minh tứ giác AHMK là hình chữ nhật
b) Gọi N là điểm đối xứng của M qua K. Chứng minh tứ giác AMCN là hình thoi
c)Cho AC=12cm ; BC=15cm. Tính diện tích tam giác ABC
bạn nào giúp mình với sắp thi học kì rồi :(((
Cho tam giác vuông ABC vuông tại A, biết AB= 6cm, AC=8 cm. M là trung điểm của BC kẻ ME vuông góc AC( E thuộc AC), MD vuông góc AB( D thuộc AB)
a) tính BC và diện tích của tam giác ABC?
b) Chứng minh tứ giác AHMK là hình chữ nhật
c) Xác định vị trí M trên cạnh BC để hình chữ nhật AHMK là hình vuông?
Bài 1:Cho hình thang ABME(AB//ME) Â=90 độ , C là trung điểm của BM. Từ C vẽ CK vuông góc với AE(K thuộc AE). Tính CK biết AB=10cm và ME=14cm
Bài 2:
Cho tam giác ABC vuông tại A(AB<AC), M tuỳ ý trên cạnh BC. Kẻ MH vuông góc AB , MK vuông góc AC ( H thuộc AB và K thuộc AC)
a) Ch/minh :tứ giác AHMK là hình chữ nhật
b) Trên tia đối của tia KM lấy điểm D sao cho KD=MK. Ch/minh :tứ giác ADKH là hình bình hành
c) Điểm E đối xứng với M qua AB .Ch/minh : ba điểm D,A,E thẳng hàng
d) Ch/minh: EB//CD
HÌnh bạn tự vẽ nha.
1/Theo định lí đường tb của hình thang thì:
CK=\(\frac{AB+EM}{2}=\frac{10+14}{2}=12\)
2/a/Ta có:TỨ giác AHMK có \(\hept{\begin{cases}gócA=90^o\\gócH=90^o\\gócK=90^o\end{cases}}\)
MÀ AHM+HMK+MKA+KAH=3600 \(\Rightarrow\) HMK=90o
\(\Rightarrow\)Tứ Giác AHMK là HÌnh Chữ Nhật
b/c/d/cm đó dễ mà bạn tự làm đi.