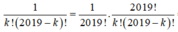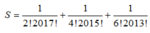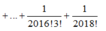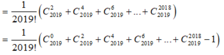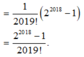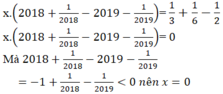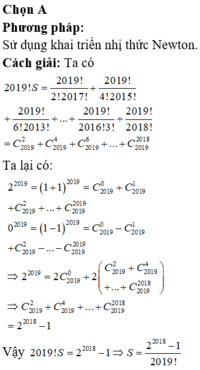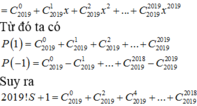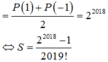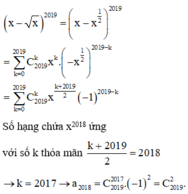|-2017|+12018(|-2018|+20160)

Những câu hỏi liên quan
Tính tổng S
1
2
!
2017
!
+
1
4
!
2015
!
+
1
6
!
2013
!
+
.
.
.
.
...
Đọc tiếp
Tính tổng S = 1 2 ! 2017 ! + 1 4 ! 2015 ! + 1 6 ! 2013 ! + . . . . + 1 2016 ! 3 ! + 1 2018 !
c
B . S = 2 2018 2019 !
C . S = 2 2018 - 1 2019
D . S = 2 2018 2019
Gọi
x
0
là số thỏa mãn của
x
.
2018
-
1
2018
-
2019
-
1
2019
1
3
+...
Đọc tiếp
Gọi x 0 là số thỏa mãn của x . 2018 - 1 2018 - 2019 - 1 2019 = 1 3 + 1 6 - 1 2
A. x 0 > 0
B. x 0 < 0
C. x 0 = 0
D. x 0 = 1
Tính tổng
S
1
2
!
2017
!
+
1
4
!
2015
!
+
1
6
!
2013
!
+
.
.
.
+
1
2016...
Đọc tiếp
Tính tổng S = 1 2 ! 2017 ! + 1 4 ! 2015 ! + 1 6 ! 2013 ! + . . . + 1 2016 ! 3 ! + 1 2018 ! theo n ta được:
A. S = 2 2018 - 1 2019
B. S = 2 2018 - 1 2017
C. S = 2 2018 2017 !
D. S = 2 2018 2017
Tính tổng
S
1
2
!
2017
!
+
1
4
!
2015
!
+
1
6
!
2013
!
+
.
.
.
+
1
2016...
Đọc tiếp
Tính tổng S = 1 2 ! 2017 ! + 1 4 ! 2015 ! + 1 6 ! 2013 ! + . . . + 1 2016 ! 3 ! + 1 2018 ! theo n ta được
![]()
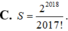
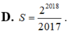
Tính tổng
S
1
2
!
2017
!
+
1
4
!
2015
!
+
1
6
!
2013
!
+
.
.
.
+
1
2016...
Đọc tiếp
Tính tổng S = 1 2 ! 2017 ! + 1 4 ! 2015 ! + 1 6 ! 2013 ! + . . . + 1 2016 ! 3 ! + 1 2018 ! theo n ta được:
A. S = 2 2018 - 1 2019 !
B. S = 2 2018 - 1 2017
C. S = 2 2018 2017 !
D. S = 2 2018 2017
Chọn A
Phương pháp: Sử dụng khai triển nhị thức Newton.
Cách giải: Ta có
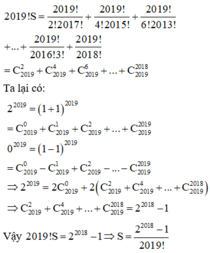
Đúng 0
Bình luận (0)
Tinh nhanh:
2017 2017 2017 x 2018 2018 2018 2018 /2018 2018 2018 x 2017 2017 2017 2017
Tinh nhanh:
2017 2017 2017 x 2018 2018 2018 2018 /2018 2018 2018 x 2017 2017 2017 2017
Giúp mình nha!!!!!!!!!!!
\(=\frac{2018}{2017}\)
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~
Đúng 0
Bình luận (0)
giải ra hộ mình nha các bạn ra kết quả như thế là sai rùi thử tính máy tính đi
Đúng 0
Bình luận (0)
Gọi
a
2018
là hệ số của số hạng chứa
x
2018
trong khai triển nhị thức Niutơn
x
−
x
n
với
x
≥
0
; n là số nguyên dương thỏa mãn
1
2
!
.2017
!...
Đọc tiếp
Gọi a 2018 là hệ số của số hạng chứa x 2018 trong khai triển nhị thức Niutơn x − x n với x ≥ 0 ; n là số nguyên dương thỏa mãn 1 2 ! .2017 ! + 1 4 ! .2015 ! + 1 6 ! .2013 ! ... + 1 2016 ! .3 ! + 1 2018 ! = 2 2018 − 1 P n . Tìm a 2018
A. 2017
B. − C 2018 3 .
C. 2019
D. C 2019 2 .
CMR \(\left(2018^{2017}+2017^{2017}\right)^{2018}>\left(2018^{2018}+2017^{2018}\right)^{2017}\)
Có: \(\left(2018^{2018}+2017^{2018}\right)^{2017}< \left(2018^{2017}.2018+2017^{2017}.2018\right)^{2017}\)
\(=\left(2018^{2017}+2017^{2017}\right)^{2017}.2018^{2017}< \left(2018^{2017}+2017^{2017}\right)^{2017}.\left(2018^{2017}+2017^{2017}\right)\)
\(=\left(2018^{2017}+2017^{2017}\right)^{2018}\)
Cho hai số A = (2018^2017 + 2017^2017)^2018 ; B = (2018^2018 + 2017^2018)^2017. so sánh A và B
\(A=\left(2018^{2017}+2017^{2017}\right)^{2018}\) ; \(B=\left(2018^{2018}+2017^{2018}\right)^{2017}\)
Ta có:
\(B=\left(2018.2018^{2017}+2017.2017^{2017}\right)^{2017}\)
\(\Rightarrow B< \left(2018.2018^{2017}+2018.2017^{2017}\right)^{2017}\)
\(\Rightarrow B< \left(2018^{2017}+2017^{2017}\right)^{2017}.2018^{2017}\)
\(\Rightarrow B< \left(2018^{2017}+2017^{2017}\right)^{2017}.\left(2018^{2017}+2017^{2017}\right)\)
\(\Rightarrow B< \left(2018^{2017}+2017^{2017}\right)^{2018}=A\)
\(\Rightarrow B< A\)
Đúng 0
Bình luận (0)