(x-2).(y-1)=-11
Những câu hỏi liên quan
Cho \(x=\dfrac{1-\sqrt{3}}{2};y=\dfrac{-1-\sqrt{3}}{2}\). Tính \(x^{11}+y^{11}\)
Lời giải:
Ta có \(x+y=-\sqrt{3}; xy=\frac{1}{2}\)
\(x^{11}+y^{11}=(x^5+y^5)(x^6+y^6)-x^5y^5(x+y)=(x^5+y^5)(x^6+y^6)+\frac{\sqrt{3}}{32}\)
Nhận thấy:
\(x^2+y^2=(x+y)^2-2xy=3-2.\frac{1}{2}=2\)
\(x^3+y^3=(x+y)^3-3xy(x+y)=-3\sqrt{3}+\frac{3\sqrt{3}}{2}=-1,5\sqrt{3}\)
\(x^5+y^5=(x^2+y^2)(x^3+y^3)-x^2y^2(x+y)\)
\(=-3\sqrt{3}+\frac{1}{4}\sqrt{3}=\frac{-11}{4}\sqrt{3}\)
\(x^6+y^6=(x^3+y^3)^2-2(xy)^3=(-1,5\sqrt{3})^2-2.\frac{1}{8}=\frac{13}{2}\)
Do đó: \(x^{11}+y^{11}=\frac{-11}{4}\sqrt{3}.\frac{13}{2}+\frac{\sqrt{3}}{32}=\frac{-571}{32}\sqrt{3}\)
Đúng 0
Bình luận (0)
Cho \(x=\dfrac{-1+\sqrt{3}}{2};y=\dfrac{-1-\sqrt{3}}{2}\). Tính \(x^{11}+y^{11}\)
Ta có : x+y= -1 và xy= \(\dfrac{-1}{2}\)
x2+y2= (x+y)2-2xy=1-1=0
x4+y4 = (x2+y2)2-2x2y2=0+\(\dfrac{1}{2}\)=\(\dfrac{1}{2}\)
x8+y8=(x4+y4)2-2x4y4=\(\dfrac{1}{4}\)-\(\dfrac{1}{8}\)=\(\dfrac{1}{8}\)
x3+y3=(x+y)3-3xy(x+y)=-1\(-\dfrac{3}{2}\) =\(\dfrac{-1}{2}\)
x11+y11=(x8+y8)(x3+y3)-x3y3(x5+y5)=\(\dfrac{1}{8}\).\(\dfrac{-1}{2}\)+\(\dfrac{1}{8}\)(x5+y5)
Bạn tính x5+y5 rồi thế vô ( Tính x3+y3 và x2+y2 rồi làm giống cách trên chứ dài quá mình viết không nổi )
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho bốn đường thẳng
d
1
:
x
-
3
1
y
+
1
-
2
z
+
1
1
;
d
2
:
x
1
y
-
2...
Đọc tiếp
Trong không gian Oxyz, cho bốn đường thẳng d 1 : x - 3 1 = y + 1 - 2 = z + 1 1 ; d 2 : x 1 = y - 2 = z - 1 1 ; d 3 : x - 1 2 = y + 1 1 = z - 1 1 ; d 4 : x 1 = y - 1 - 1 = z - 1 1 . Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A. 0.
B. 2.
C. Vô số.
D. 1.
Chọn D
Đường thẳng d₁ đi qua điểm M₁ = (3;-1;-1) và có một véctơ chỉ phương là 
Đường thẳng d₂ đi qua điểm M₂ = (0;0;1) và có một véctơ chỉ phương là 
Do 
và M₁ ∉ d₁ nên hai đường thẳng d₁ và d₂ song song với nhau.
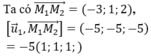
Gọi (α) là mặt phẳng chứa d₁ và d₂ khi đó (α) có một véctơ pháp tuyến là 
. Phương trình mặt phẳng (α) là x+y+z-1=0.
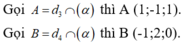
Do 
không cùng phương với 
nên đường thẳng AB cắt hai đường thẳng d₁ và d₂.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho bốn đường thẳng:
d
1
:
x
-
3
1
y
+
1
-
2
z
+
1
1
,
d
2
:...
Đọc tiếp
Trong không gian Oxyz, cho bốn đường thẳng:
d 1 : x - 3 1 = y + 1 - 2 = z + 1 1 , d 2 : x 1 = y - 2 = z - 1 1 , d 3 : x - 1 2 = y + 1 1 = z - 1 1 , d 4 : x 1 = y - 1 - 1 = z - 1 1
Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A. 0.
B. 2.
C. Vô số.
D. 1.
Chọn D
Đường thẳng d1 đi qua điểm M1 (3; -1; -1) và có một véctơ chỉ phương là 
Đường thẳng d2 đi qua điểm M2 (0; 0; 1) và có một véctơ chỉ phương là 
Do 
và M1 ∉ d1 nên hai đường thẳng d1 và d2 song song với nhau.
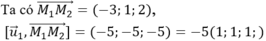
Gọi (α) là mặt phẳng chứa d1 và d2 khi đó (α) có một véctơ pháp tuyến là 
Phương trình mặt phẳng (α) là x + y + z -1 = 0
Gọi A = d3 ∩ (α) thì A (1; -1; 1)
Gọi B = d4 ∩ (α) thì B (-1; 2; 0)
Do 
không cùng phương với 
nên đường thẳng AB cắt hai đường thẳng d1 và d2.
Đúng 0
Bình luận (0)
ai giúp em với gấp lắm rồi: mong các bác cho lời giải ko ghi đáp án chống đối
1.Tìm các số hữu tỉ x,y,z biết:
a) x.(x-y+z)=11 ; y.(y-z-x)=25 ; z.(z+x-y)=35
b) (x+2)^2 + (y-3)^4 + (z-5)^6=0
2. So sánh A và B biết
a) A=-1/2011 - 3/11^2 - 5/11^3 - 7/11^4 và B= -1/2011 - 7/11^2 - 5/11^3 - 3/11^4
b) A= 2006/2007 - 2007/2008 + 2008/2009 - 2009/2010 và B= -1/2006.2007 - 1/2008.2009
mong mấy bạn giúp mình mai mình nộp rôì ko đùa đâu
Đúng 0
Bình luận (0)
ai lam guip toi cau nay voi mai toi nop bai roi
so sanh 2 phan so sau bang cach nahnh nhat: 2007/2008 voi 2008/2009
Đúng 0
Bình luận (0)
1. so sánh các tích sau bằng cách hợp lý nhất :P1 ( -57/95 ) . ( -29/60 ) P2 ( -5/11 ) . ( -49/73 ) . ( -6/23 ) P3 -4/11 . -3/11 . -2/11 ........ 3/11 . 4/11 2. tìm các số nguyên x, y bt rằng : x/4 - 1/y 1/2 3. tìm 2 số hữu tỉ x và y sao cho x - y x . y x : y ( y ne0 ) 4. tìm các số hữu tỉ x, y, z bt rằng : x . ( x + y + z ) -5 y . ( x + y + z ) 9 z . ( x + y + z ) 5
Đọc tiếp
1. so sánh các tích sau bằng cách hợp lý nhất :
P1 = ( -57/95 ) . ( -29/60 )
P2 = ( -5/11 ) . ( -49/73 ) . ( -6/23 )
P3 = -4/11 . -3/11 . -2/11 ........ 3/11 . 4/11
2. tìm các số nguyên x, y bt rằng :
x/4 - 1/y = 1/2
3. tìm 2 số hữu tỉ x và y sao cho x - y = x . y = x : y ( y \(\ne\)0 )
4. tìm các số hữu tỉ x, y, z bt rằng :
x . ( x + y + z ) = -5
y . ( x + y + z ) = 9
z . ( x + y + z ) = 5
Trong không gian với hệ trục tọa độ , cho bốn đường thẳng:
d
1
:
x
-
3
1
y
+
1
-
2
z
+
1
1
;
d
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ , cho bốn đường thẳng:
d 1 : x - 3 1 = y + 1 - 2 = z + 1 1 ; d 2 : x 1 = y - 2 = z - 1 1
d 3 : x - 1 2 = y + 1 1 = z - 1 1 ; d 4 : x 1 = y - 1 - 1 = z - 1
Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A. 0
B. 2
C. Vô số.
D. 1
Chọn A
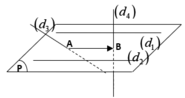
Ta có d1 song song d2, phương trình mặt phẳng chứa hai đường thẳng d1, d2 là
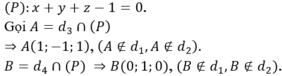
Mà 
cùng phương với véc-tơ chỉ phương của hai đường thẳng d1, d2 nên không tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
Đúng 0
Bình luận (0)
tìm x,y,z biết |x-11|+|x-8|^1981+|x+1|=48/(|y-2|+|y-1|+|y+2|)
22 tháng 2 2022 lúc 18:25
1. Giải phương trình sau:x^3-3x^2+2sqrt{left(x+2right)^3}-6x02. Cho các số thực x,y thỏa mã điều kiện:sqrt{x^2+11}+sqrt{x^2-2018}+x^2sqrt{y^2+11}+sqrt{y^2-2018}+y^2Tính giá trị biểu thức: Mx^{11}-y^{2018}3. Cho tam giác ABC vuông tại A trên cạnh BC lấy điểm D bất kỳ. Gọi E và F lần lượt là hình chiếu của D trên cạnh AB và AC.a) CM: DB.DCEA.EB+FA.FCb) Trên cạnh BC lấy điểm M sao cho ^BAD^CAMCMR: dfrac{DB}{DC}.dfrac{MB}{MC}dfrac{AB^2}{AC^2}
Đọc tiếp
1. Giải phương trình sau:
\(x^3-3x^2+2\sqrt{\left(x+2\right)^3}-6x=0\)
2. Cho các số thực x,y thỏa mã điều kiện:
\(\sqrt{x^2+11}+\sqrt{x^2-2018}+x^2=\sqrt{y^2+11}+\sqrt{y^2-2018}+y^2\)
Tính giá trị biểu thức: \(M=x^{11}-y^{2018}\)
3. Cho tam giác ABC vuông tại A trên cạnh BC lấy điểm D bất kỳ. Gọi E và F lần lượt là hình chiếu của D trên cạnh AB và AC.
a) CM: DB.DC=EA.EB+FA.FC
b) Trên cạnh BC lấy điểm M sao cho ^BAD=^CAM
CMR: \(\dfrac{DB}{DC}.\dfrac{MB}{MC}=\dfrac{AB^2}{AC^2}\)
1.
đk: \(x\ge2\)
Đặt y = \(\sqrt{x+2}\) ta biến pt về dạng pt thuần nhất bậc 3 đối vs x và y:
ta có : \(x^3-3x^2+2y^3-6x=0\)
\(\Leftrightarrow x^3-3xy^2+2y^3=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=y\\x=-2y\end{matrix}\right.\)
ta sẽ có nghiệm : \(x=2;x=2-2\sqrt{3}\)
\(1.đk:\left(x+2\right)^3\ge0\Leftrightarrow x\ge-2\)
\(pt\Leftrightarrow x^3-3x\left(x+2\right)+2\sqrt{\left(x+2\right)^3}=0\)
\(\Leftrightarrow x^3-x\left(x+2\right)+2\sqrt{\left(x+3\right)^2}-2x\left(x+2\right)=0\)
\(\Leftrightarrow x\left[x^2-\left(x+2\right)\right]+2\left(x+2\right)\left(\sqrt{x+2}-x\right)=0\)
\(\Leftrightarrow x\left[\left(x-\sqrt{x+2}\right)\left(x+\sqrt{x+2}\right)\right]+2\left(x+2\right)\left(\sqrt{x+2}-x\right)=0\)
\(\Leftrightarrow\left(\sqrt{x+2}-x\right)\left[-x\left(\sqrt{x+2}+x\right)+2\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(\sqrt{x+2}-x\right)^2\left(2\sqrt{x+2}+x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+2}=x\left(2\right)\\2\sqrt{x+2}=-x\left(3\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2=x+2\end{matrix}\right.\)\(\Leftrightarrow x=2\left(tm\right)\)
\(\left(3\right)\Leftrightarrow\left\{{}\begin{matrix}-x\ge0\Leftrightarrow x\le0\\x^2=4\left(x+2\right)\end{matrix}\right.\)\(\Leftrightarrow x=2-2\sqrt{3}\left(tm\right)\)
Đúng 4
Bình luận (1)
\(2.đk:x^2;y^2\ge2018\Leftrightarrow\left[{}\begin{matrix}x;y\le-\sqrt{2018}\\x;y\ge\sqrt{2018}\end{matrix}\right.\)
\(pt\Leftrightarrow\sqrt{x^2+11}-\sqrt{y^2+11}+\sqrt{x^2-2018}-\sqrt{y^2-2018}+x^2-y^2=0\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)+\dfrac{x^2+11-y^2-11}{\sqrt{x^2+11}+\sqrt{y^2+11}}+\dfrac{x^2-2018-y^2+2018}{\sqrt{x^2-2018}+\sqrt{y^2-2018}}=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)\left[1+\dfrac{1}{\sqrt{x^2+11}+\sqrt{y^2+11}}+\dfrac{1}{\sqrt{x^2-2018}+\sqrt{y^2+2018}}>0\right]=0\Leftrightarrow\left[{}\begin{matrix}x=y\\x=-y\end{matrix}\right.\)
\(x=y\Rightarrow M=x^{11}-x^{2018}\)
\(x=-y\Rightarrow M=-y^{11}-y^{2018}=:vvv\) (đến đây chịu)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
tìm các số nguyên x,y biết : 1/x-y/11=-2/11
\(\frac{1}{x}-\frac{y}{11}=\frac{-2}{11}\)
Ta thấy cả số trừ và hiệu đều mẫu số là 11
=> mẫu số số bị trừ là 11 ; x = 11
Ta có
\(\frac{1}{11}-\frac{y}{11}=-\frac{2}{11}\)
\(\frac{y}{11}=-\frac{2}{11}-\frac{1}{11}\)
\(\frac{y}{11}=\frac{3}{11}\)
=> y = 3
Đúng 0
Bình luận (0)
\(\frac{1}{x}-\frac{y}{11}=\frac{-2}{11}\)
\(\frac{11}{11x}-\frac{y}{11}=\frac{-2}{11}\)
\(\frac{11}{11x}=\frac{-2+y}{11}\)
\(\frac{1}{x}=\frac{-2+y}{11}\)
1 . 11 = ( - 2 + y ) . x
11 = ( - 2 + y ) . x
| -2 + y | 11 | 1 | -11 | -1 |
| 3 | 1 | 11 | 1 | 11 |
=> Nếu -2 + y = 11 thì y = 13 và x = 1
=> Nếu -2 + y = 1 thì y = 3 và x = 11
=> Nếu -2 + y = -11 thì y = -9 và x = 1
=> Nếu -2 + y = -1 thì y = 1 và x = 11
Đúng 0
Bình luận (0)