Tìm giá trị nguyên của x để Px ⋮ Qx biết
Px = x3 - x2 +2
Qx = x - 1
Px= \(-2x^2+3x^4-9x^3-\dfrac{1}{4}x+2x^5\)
Qx=\(4x^2+3x^4-2x^3-2x^5-\dfrac{1}{4}\)
a. Tính Px +Qx và tính Px-Qx
b. x=0 là nghiệm của đa thức Px hay Qx? Vì sao?
c. Tính giá trị của Qx khi x= -1
giúp mk vs
a: \(P\left(x\right)+Q\left(x\right)=6x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
\(P\left(x\right)-Q\left(x\right)=4x^5-7x^3-6x^2-\dfrac{1}{4}x+\dfrac{1}{4}\)
b: \(P\left(0\right)=-2\cdot0^2+3\cdot0^4-9\cdot0^3-\dfrac{1}{4}\cdot0+2\cdot0^5=0\)
=>x=0 là nghiệm của P(x)
\(Q\left(0\right)=4\cdot0+3\cdot0-2\cdot0-2\cdot0-\dfrac{1}{4}=\dfrac{-1}{4}\)
=>x=0 không là nghiệm của Q(x)
c: \(Q\left(-1\right)=4\cdot1+3\cdot1-2\cdot\left(-1\right)-2\cdot\left(-1\right)-\dfrac{1}{4}\)
\(=7+2+2-\dfrac{1}{4}=11-\dfrac{1}{4}=\dfrac{43}{4}\)
cho 2 đa thức Px và Qx. Biết P(1)=1 và P(-2)=7 và Px chia cho (x-1)(x+2) được thương là 2x và còn dư. đa thức Qx=x*4-4x*3-3x*2+8x-2.tính Px +Qx -12.biết x(x-1)=46
1.cho đa thức: Px=x⁴-2x³+x-5+/3x/-2x+2x³ Qx=(2x²-x³)-(2-x⁴-x³)-3x a) Thu gọn đa thức Px,Qx và sắp xếp các hạng tử của mỗi đa thức theo lúy thùa giảm dần của biến. b) tính Ax=Px-Qx c) chứng tỏ x=1 là một nghiệm của đa thức Ax
a) Để thu gọn đa thức Px, ta sắp xếp các hạng tử theo lũy thừa giảm dần của biến x:
Px = x⁴ - 2x³ + x - 5 + / 3x / -2x + 2x³ = x⁴ + 2x³ - 2x³ + x + / 3x / -2x = x⁴ + (2x³ - 2x³) + (x + / 3x / -2x) = x⁴ + (x + / 3x / -2x)
Tương tự, để thu gọn đa thức Qx, ta sắp xếp các hạng tử theo lũy thừa giảm dần của biến x:
Qx = (2x² - x³) - (2 - x⁴ - x³) - 3x = -x³ + 2x² - 2 + x⁴ + x³ - 3x = x⁴ + (-x³ + x³) + 2x² - 3x - 2 = x⁴ + 2x² - 3x - 2
b) Để tính Ax = Px - Qx, ta trừ từng hạng tử của Qx từ Px:
Ax = (x⁴ + (x + / 3x / -2x)) - (x⁴ + 2x² - 3x - 2) = x⁴ + x + / 3x / -2x - x⁴ - 2x² + 3x + 2 = x⁴ - x⁴ + x + / 3x / -2x - 2x² + 3x + 2 = x + / 3x / -2x - 2x² + 3x + 2
c) Để chứng tỏ x = 1 là một nghiệm của đa thức Ax, ta thay x = 1 vào Ax và kiểm tra xem kết quả có bằng 0 hay không:
Ax = 1 + / 3(1) / -2(1) - 2(1)² + 3(1) + 2 = 1 + 3/2 - 2 + 3 + 2 = 6.5
Vì Ax không bằng 0 khi thay x = 1, nên x = 1 không phải là một nghiệm của đa thức Ax.
a: P(x)=x^4-2x^3+x+2x^3-2x-5+3x
=x^4-x+3x-5
=x^4+2x-5
Q(x)=2x^2-x^3-2+x^4+x^3-3x
=x^4+2x^2-3x-2
b: A(x)=P(x)-Q(x)
=x^4+2x-5-x^4-2x^2+3x+2
=-2x^2+5x-3
c: A(1)=-2+5-3=0
=>x=1 là nghiệm của A(x)
Cho đa thức : Px = \(48x^4-28x^3-24x^2+mx+1\) và Qx= \(2x^2+nx+1\)
a, Tìm m , n (dưới dạng phân số hoặc số nguyên ) để đa thức Px chia hết cho đa thức Qx
b, Với m vừa tìm được ở câu a, hãy tìm các nghiệm của Px(lấy 4 chữ số thập phân)
biết rằng phương trình \(x^2+px+1=0\) có nghiệm là a,b và phương trình \(x^2+qx+2=0\) có nghiêm là b,c . Khi đó giá trị của biểu thức \(A=pq-\left(b-a\right)\left(b-c\right)\)bằng ?
Áp dụng viet vào pt \(x^2+px+1=0\) ta được:\(\left\{{}\begin{matrix}a+b=-p\\ab=1\end{matrix}\right.\)
Áp dụng viet vào pt \(x^2+qx+2=0\) ta được:\(\left\{{}\begin{matrix}b+c=-q\\bc=2\end{matrix}\right.\)
\(A=pq-\left(b-a\right)\left(b-c\right)=-\left(a+b\right).-\left(b+c\right)-\left(b^2-bc-ab+ac\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
\(=2ab+2bc=6\)
Phương trình: \(x^2+px+1=0\)
Có 2 nghiệm:a,b
\(\Rightarrow\left\{{}\begin{matrix}a+b=-p\\a.b=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}p=-\left(a+b\right)\\1=a.b\end{matrix}\right.\)
Phương trình \(x^2+px+2=0\)
Có 2 nghiệm:b,c
\(\Rightarrow\left\{{}\begin{matrix}b+c=-q\\b.c=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}q=-\left(b+c\right)\\2=b.c\end{matrix}\right.\)
Ta có: \(p.q-\left(b-a\right)\left(b-c\right)\)
\(=-\left(a+b\right).\left[-\left(b+c\right)\right]-\left(b-a\right)\left(b-c\right)\)
\(=\left(a+b\right)\left(b+c\right)-\left(b-a\right)\left(b-c\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
=\(\left(ab+ab\right)+\left(ac-ac\right)+\left(b^2-b^2\right)+\left(bc+bc\right)\)
\(=2ab+2bc\)
\(=2.1+2.2\)
=6
-Chúc bạn học tốt-
Cho hai đa thức:
P x = x 5 - 3 x 2 + 7 x 4 - 9 x 3 + x 2 - 1 4 x
Q x = 5 x 4 - x 5 + x 2 - 2 x 3 + 3 x 2 - 1 4
Tính P(x) + Q(x) và P(x) – Q(x).
Ta đặt và thực hiện các phép tính P(x) + Q(x) và P(x) – Q(x).

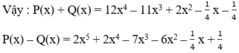
Tìm x ∈ N, biết:
a, x ∈ B(5), x < 20
b, x ⋮ 24; x ⋮ 45; 200 < x < 500
c, 452 = px+32; 321 = qx+21 (p,q ∈ N*)
a, Ta có: x ∈ B(5) = {0;5;10;15;20;25;...}
Mà x < 20 => x ∈ {0;5;10;15}
b, Ta có: x ⋮ 24; x ⋮ 45 => x ∈ BC{24;45}
24 = 2 3 . 3 ; 45 = 3 2 . 5 => BCNN(24;45) = 2 3 . 3 2 . 5 = 360
=> BC(24;45) = B(360) = {0;360;720;...}
Mà 200 < x < 500 => x = 360
c, Ta có:
452 = px+32 => 420 ⋮ x
321 = qx+21 => 320 ⋮ x
=> x ∈ ƯC(420;320)
420 = 2 2 . 3 . 5 . 7
320 = 2 6 . 5
=> ƯCLN(420;320) = 20 = 2 2 . 5
=> ƯC(420;320) = Ư(20) = {1;2;4;5;10;20}
Vậy x ∈ {1;2;4;5;10;20}
Biết rằng phương trình \(x^2+px+1\) có 2 nghiệm là a,b và phương trình \(x^2+qx+2\) có 2 nghiệm là b,c. Tính giá trị của biểu thức A = pq - (b-a) (b-c)
Cho hai đa thức:
P x = x 5 - 3 x 2 + 7 x 4 - 9 x 3 + x 2 - 1 4 x
Q x = 5 x 4 - x 5 + x 2 - 2 x 3 + 3 x 2 - 1 4
Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x)