\(a,\) Pt hoành độ giao điểm 

\(x=0\\ \Leftrightarrow y=-2\cdot0+3=3\\ \Leftrightarrow A\left(0;3\right)\)

Pt tung độ giao điểm

\(y=0\\ \Leftrightarrow0=-2x+3\Leftrightarrow x=\dfrac{3}{2}\\ \Leftrightarrow B\left(\dfrac{3}{2};0\right)\)

Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=\sqrt{5}\)

Điểm M thuộc (C) thỏa mãn khoảng cách từ M tới \(\Delta\) lớn nhất khi M là giao điểm của (C) và đường thẳng d qua I và vuông góc \(\Delta\)

Phương trình d có dạng:

\(2\left(x-1\right)-1\left(y+2\right)=0\Leftrightarrow2x-y-4=0\)

Hệ pt tọa độ giao điểm (C) và d:

\(\left\{{}\begin{matrix}x^2+y^2-2x+4y=0\\y=2x-4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+\left(2x-4\right)^2-2x+4\left(2x-4\right)=0\\y=2x-4\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x=0\\y=2x-4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(0;-4\right)\\M\left(2;0\right)\end{matrix}\right.\)

Với \(M\left(0;-4\right)\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|-2.4+7\right|}{\sqrt{1^2+2^2}}=\dfrac{1}{\sqrt{5}}\)

Với \(M\left(2;0\right)\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|2+0+7\right|}{\sqrt{1^2+2^2}}=\dfrac{9}{\sqrt{5}}\)

Do \(\dfrac{9}{\sqrt{5}}>\dfrac{1}{\sqrt{5}}\) nên \(M\left(2;0\right)\) là điểm cần tìm

\(1/\)

\(M\left(3;5\right);d:x+y+1=0\)

\(\)Gọi khoảng cách từ M đến d là \(l\)

\(l\left(M;d\right)=\dfrac{\left|x_M+y_M+1\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|3+5+1\right|}{\sqrt{1^2+1^2}}=\dfrac{9\sqrt{2}}{2}\)

\(M\left(2;3\right);d:\left\{{}\begin{matrix}x-2t\\y=2+3t\end{matrix}\right.\)

d qua \(M\left(2;3\right)\) có \(VTCP\overrightarrow{u}=\left(-2;3\right)\Rightarrow VTPT\overrightarrow{n}=\left(3;2\right)\)

\(PTTQ\) của \(\Delta:3\left(x-2\right)+2\left(y-3\right)=0\)

\(\Rightarrow3x-6+2y-6=0\)

\(\Rightarrow3x+2y-12=0\)

Gọi khoảng cách từ M đến d là \(l\)

\(l\left(M;d\right)=\dfrac{\left|3.x_M+2.y_M-12\right|}{\sqrt{3^2+2^2}}=\dfrac{\left|3.2+2.3-12\right|}{\sqrt{3^2+2^2}}=0\)

* Giao điểm với trục Ox:

Ta có: -2x + 3 = 0

⇔ 2x = 3

⇔ x = 3/2

⇒ A(3/2; 0) là giao điểm với trục Ox

* Giao điểm với trục Oy:

x = 0 ⇔ y = 3

⇒ B(0; 3) là giao điểm với trục Oy

* Khoảng cách từ O(0; 0) tới (d):

Xét đồ thị:

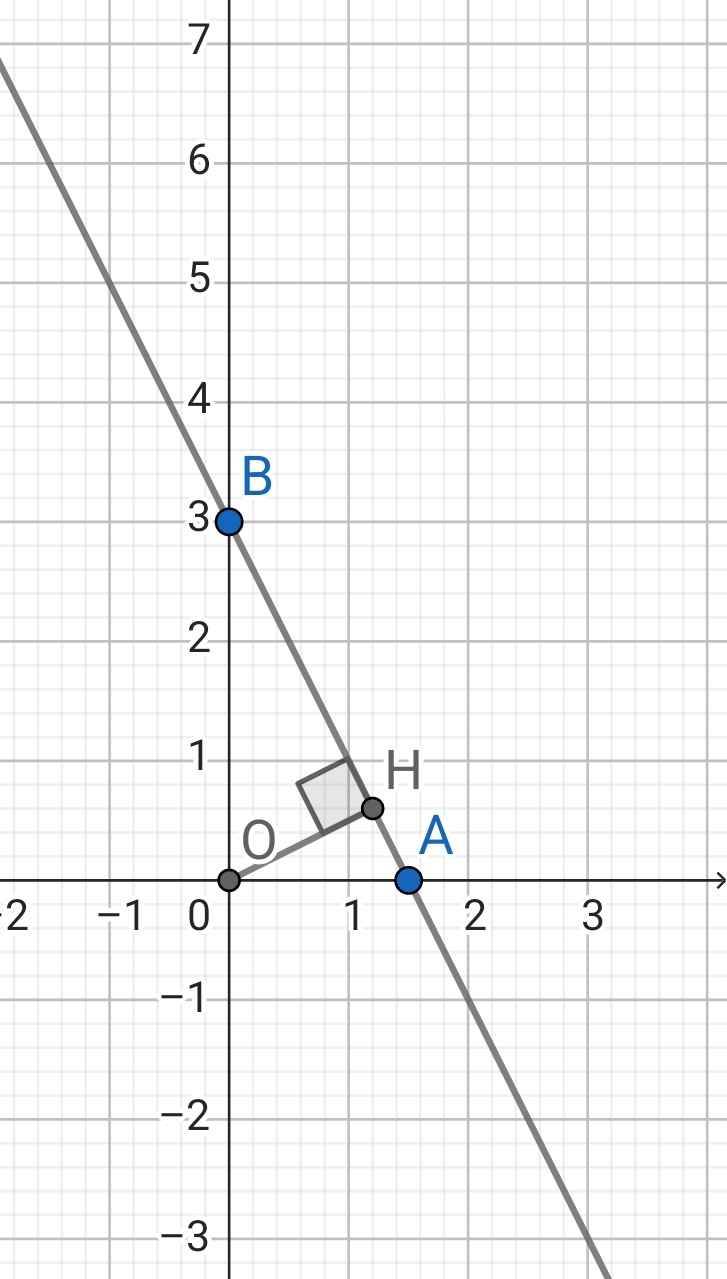 Ta có:

AB² = OA² + OB² (Pytago)

= (3/2)² + 3²

= 45/4

⇒ AB = 3√5/2

Khoảng cách từ O đến (d) là đoạn thẳng OH

Ta có:

OH.AB = OA.OB

⇒ OH = OA.OB : AB

= 3/2 . 3 : (3√5/2)

= 3/√5

khoảng cách là \(\dfrac{3}{\sqrt{5}}\) 

a/ Tọa độ A là nghiệm của hệ

\(\hept{\begin{cases}y=-2x+3\\y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1,5\\y=0\end{cases}}\)

=> A(1,5; 0)

Tọa độ B là nghiệm của hệ

\(\hept{\begin{cases}x=0\\y=-2x+3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=3\end{cases}}\)

=> B(0; 3)

Khoản cách từ O(0; 0) đến d

\(=\frac{\left|0-2×0-3\right|}{\sqrt{1^2+2^2}}=\frac{3}{\sqrt{5}}\)

b/ Khoản cách từ C(0; - 2) đến d là

\(d\left(C,d\right)=\frac{\left|-2+2×0-3\right|}{\sqrt{1^2+2^2}}=\frac{5}{\sqrt{5}}=\sqrt{5}\)

A/ TỌA ĐỘ A THỎA \(\hept{\begin{cases}Y=0\\Y=-2X+3\end{cases}}\)\(\Rightarrow\Rightarrow A\left(\frac{3}{2},O\right)\)

TỌA ĐỘ B THỎA,\(\hept{\begin{cases}Y=-2X+3\\X=0\end{cases}}\)\(\Rightarrow B\left(0,3\right)\)

GOI H LA HINH CHIEU CUA O LEN (d) ap dung he thuc luong trong tam giac vuongOAB cho

\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\Leftrightarrow\frac{1}{OH^2}=\frac{1}{\left(\frac{3}{2}\right)^2}+\frac{1}{3^2}\Rightarrow AH=\frac{3}{\sqrt{5}}\)

B/GỌI K LÀ HÌNH CHIẾU CỦA C LÊN (d) ta co\(\frac{OH}{CK}=\frac{OB}{OC}=\frac{3}{5}\Rightarrow CK=\frac{5}{3}OH=\sqrt{5}\)

(....20 NHA)

Cảm ơn bạn alibaba nguyễn ! Mk có án 20 sao nó lại chỉ đc 1 nhỉ ?  @@

A là giao điểm AB và AC nên tọa độ thỏa mãn:

\(\left\{{}\begin{matrix}2x+y-5=0\\x-3y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\) \(\Rightarrow A\left(2;1\right)\)

\(d\left(A;...\right)=\dfrac{\left|7.2-8.1+26\right|}{\sqrt{7^2+\left(-8\right)^2}}=\dfrac{32}{\sqrt{113}}\)

Do \(M\in d_3\) \(\Rightarrow M\left(2a;a\right)\)

\(\frac{\left|2a+a+3\right|}{\sqrt{1^2+1^2}}=2\frac{\left|2a-a-4\right|}{\sqrt{1^2+\left(-1\right)^2}}\Leftrightarrow\left|3a+3\right|=2\left|a-4\right|\)

\(\Leftrightarrow\left(3a+3\right)^2=4\left(a-4\right)^2\Leftrightarrow9a^2+18a+9=4a^2-32a+64\)

\(\Leftrightarrow5a^2+50a-55=0\Rightarrow\left[{}\begin{matrix}a=1\\a=-11\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(2;1\right)\\M\left(-22;-11\right)\end{matrix}\right.\)