hãy vẽ trục đối xứng và tâm đối xứng của tam giác đều,hình vuông (tứ giác đều), hình lục giác đều , ngũ giác đều

Những câu hỏi liên quan
Cho các mệnh đề sau:
1. Tam giác đều có 3 trục đối xứng và 1 tâm đối xứng
2. Hình vuông có 4 trục đối xứng và 1 tâm đối xứng
3. Ngũ giác đều có 5 trục đối xứng và 1 tâm đối xứng
4. Lục giác đều có 6 trục đối xứng và 1 tâm đối xứng
Số mệnh đềđúng là:
A.1
B.2
C.3
D.4
Các phát biểu nào sai?
A. Hình tròn có vô số trục đối xứng và 1 tâm đối xứng
B. Hình vuông có 4 trục đối xứng
C. Hình tam giác đều có 3 trục đối xứng 1 tâm đối xứng
D. Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng
Các phát biểu về đối xứng hình học như sau:
A. Hình tròn: Hình tròn có vô số trục đối xứng và 1 tâm đối xứng. Điều này đúng.
B. Hình vuông: Hình vuông có 4 trục đối xứng, tương ứng với 4 đường đối xứng qua các đỉnh của hình vuông. Điều này cũng đúng.
C. Hình tam giác đều: Hình tam giác đều có 3 trục đối xứng và 1 tâm đối xứng. Điều này cũng đúng.
D. Hình lục giác đều: Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng, tương ứng với 6 đường đối xứng qua các đỉnh của hình lục giác đều. Điều này cũng đúng.
Vậy tất cả các phát biểu đều đúng. 😊
Đúng 0
Bình luận (0)
Trong các hình tam giác đều, hình bình hành, ngũ giác đều, lục giác đều, hình nào có tâm, đối xứng?
Tam giác đều và ngũ giác dều không có tâm đối xứng.
* Hình bình hành có một tâm đối xứng là giao điểm của hai đường chéo.
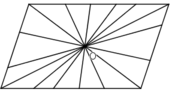
* Hình lục giác đều có một tâm đối xứng, đó là tâm đường tròn ngoại tiếp hình lục giác đều.
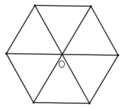
Đúng 0
Bình luận (0)
Trong các hình tam giác đều, hình bình hành, ngũ giác đều, lục giác đều, hình nào có tâm đối xứng ?
Hình bình hành và lục giác đều là những hình có tâm đối xứng.
Đúng 0
Bình luận (0)
Hình bình hành và lục giác đều là những hình có tâm đối xứng.
Đúng 0
Bình luận (0)
Hình nào dưới đây vừa có tâm đối xứng, vừa có trục đối xứng
a hình tam giác đều
b hình lục giác đều
c hình ngũ giác đều
1. Bằng cách gấp giấy, em hãy tìm một trục đối xứng của đoạn thẳng.
2. Làm tương tự như HĐ 6 với hình tam giác đều, hình vuông, hình lục giác đều. Em hãy chỉ ra một trục đối xứng của mỗi hình trên.
1. Thực hành gấp giấy: Vẽ đoạn thẳng trên tờ giấy, gấp tờ giấy theo một đường thẳng sao cho 2 đầu đoạn thẳng trùng nhau thì đường thẳng đó là một trục đối xứng.
+) Trục đối xứng của đoạn thẳng là đường thẳng thu được khi gấp giấy.
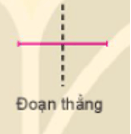
2.
+) Trục đối xứng của tam giác đều là đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện (có 3 trục đối xứng)
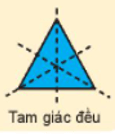
+) Trục đối xứng của hình vuông là đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông (có 4 trục đối xứng)
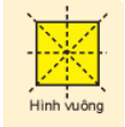
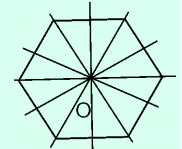
+) Trục đối xứng của lục giác đều là đường thẳng nối 1 đỉnh và tâm của lục giác đều (có 6 trục đối xứng).
Đúng 1
Bình luận (0)
a) Trục đối xứng của đoạn thẳng là đường thẳng thu được khi gấp giấy.
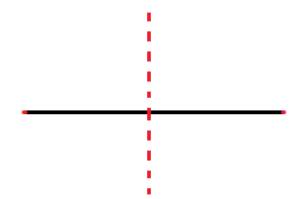
b)
+ Tam giác đều có 3 trục đối xứng là đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện
+ Hình vuông có 4 trục đối xứng là đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông
+ Hình lục giác đều có 6 trục đối xứng.
Đúng 0
Bình luận (0)
hình vuông,tròn,tam giác đều,lục giác đều có bao nhiêu trục đối xứng
hình vuông có 4 trục đối xứng
hình tròn có vô số trục đối xứng
hình tam giác đều có 3 trục đối xứng
hình lục giác đều có 6 trục đối xứng
Đúng 2
Bình luận (0)
hình vuông có : 4 trục đối xứng
hình tam giác đều có: 3 trục đối xứng
hình tròn rất nhiều trục đối xứng
hình lục giác đều có : 6 trục đối xứng
HT
Đúng 0
Bình luận (0)
Hình vuông có 4 trục
Hình tròn có vô số trục
Tam giác đều có 3 trục
Lục giác đều có 6 trục
Đúng 0
Bình luận (0)
Câu 25. Trong các hình sau, hình nào không có trục đối xứng ? A. Hình thang cân B. Hình bình hành C. Hình vuông D. Hình chữ nhật
Câu 26. Hình nào sau đây không có tâm đối xứng ? A. Hình lục giác đều B. Tam giác đều C. Hình thoi
Tính diện tích hình bình hành có độ dài đáy là 25dm và chiều cao là 18dm.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
vẽ tâm đối xứng , trục đối xứng của tam giác cân , tam giác đều ( nếu không có thì hãy chỉ rõ và giải thích )
SGK ... Tam giác cân không có tâm đối xứng đâu... Trục đối xứng của tam giác cân là ... Khó nói quá . VD nha : tam giác ABC cân tại A TH1 : kẻ AH vuông góc với BC => AH là trục đối xứng ( CM được tam giác ABH = ACH => ĐPCM) (1)
TH2 : Kẻ trung tuyến AI vì tam giác ABC cân tại A nên => AI vừa là trung tuyến vừa là đường cao => Tương tự (1)
Nhớ được các trường hợp đặc biệt của các đường trung tuyến, phân giác, đường cao ..v..v... trong tam giác cân thì cứ biện luận thôi, không cần phải giải thích nhiều vì ta công nhận điều đó là đúng ...
Đúng 0
Bình luận (0)
Em hãy cho biết trong những hình đã học như hình vuông, hình tam giác đều, hình lục giác đều, hình chữ nhật, hình bình hành, hình thoi, hình thang cân, hình nào có tâm đối xứng.
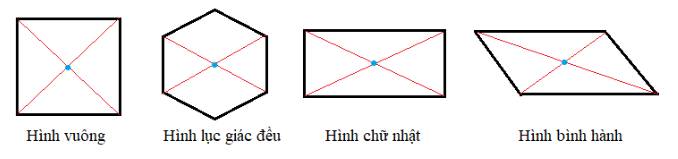
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.
Đúng 0
Bình luận (0)




























