1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)

\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}\)

\(=\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)

\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)

2) Thay \(x=4-2\sqrt{3}\) vào P, ta được:

\(P=\dfrac{2\left(\sqrt{3}-1\right)+1}{\sqrt{3}-1+1}=\dfrac{2\sqrt{3}-2+1}{\sqrt{3}}=\dfrac{2\sqrt{3}-1}{\sqrt{3}}=\dfrac{6-\sqrt{3}}{3}\)

Ký hiệu (abcd) là số tự nhiên có 4 chữ số. 
(abcd) + (abc) + (ab) + (a) = 1111.a + 111.b + 11.c + d 
Vậy 1111.a + 111.b + 11.c + d = 4321 
+ Nếu a < 3 => 111.b + 11.c + d > 2098 (vô lý vì b, c, d < 10) 
+ Nếu a > 3 => vế trái > 4321 
Vậy a = 3 => 111.b + 11.c + d = 988 
+ Nếu b < 8 => 11.c + d > 210 (vô lý vì c, d < 10) 
+ Nếu b > 8 => vế trái > 988 
Vậy b = 8 => 11.c + d = 100 
+ Nếu c < 9 => d > 11 (vô lý) 
Vậy c = 9; d = 1 
=> (abcd) = 3891

2+7+23=32

2+11+19=32

2+13+17=32

à tự mò tiếp nhé -_-

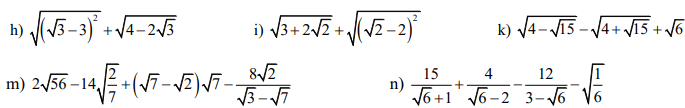
i) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}=\sqrt{\left(\sqrt{2}\right)^2+2.\sqrt{2}.1+1^2}+\left|\sqrt{2}-2\right|\)

\(=\sqrt{\left(\sqrt{2}+1\right)^2}+2-\sqrt{2}=\left|\sqrt{2}+1\right|+2-\sqrt{2}=\sqrt{2}+1+2-\sqrt{2}=3\)

k) \(\sqrt{4-\sqrt{15}}-\sqrt{4+\sqrt{15}}+\sqrt{6}=\sqrt{\dfrac{8-2\sqrt{15}}{2}}-\sqrt{\dfrac{8+2\sqrt{15}}{2}}+\sqrt{6}\)

\(=\sqrt{\dfrac{\left(\sqrt{5}\right)^2-2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}\right)^2+2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}+\sqrt{6}\)

\(=\sqrt{\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}}+\sqrt{6}\)

\(=\dfrac{\left|\sqrt{5}-\sqrt{3}\right|}{\sqrt{2}}-\dfrac{\left|\sqrt{5}+\sqrt{3}\right|}{\sqrt{2}}+\sqrt{6}\)

\(=\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}-\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{2}}+\sqrt{6}=\dfrac{-2\sqrt{3}}{\sqrt{2}}+\sqrt{6}=-\sqrt{6}+\sqrt{6}=0\)

m) \(2\sqrt{56}-14\sqrt{\dfrac{2}{7}}+\left(\sqrt{7}-\sqrt{2}\right)\sqrt{7}-\dfrac{8\sqrt{2}}{\sqrt{3}-\sqrt{7}}\)

\(=2\sqrt{4.14}-2\sqrt{49.\dfrac{2}{7}}+7-\sqrt{14}+\dfrac{8\sqrt{2}.\left(\sqrt{7}+\sqrt{3}\right)}{\left(\sqrt{7}-\sqrt{3}\right)\left(\sqrt{7}+\sqrt{3}\right)}\)

\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}+\dfrac{8.\left(\sqrt{14}+\sqrt{6}\right)}{4}\)

\(=\sqrt{14}+7+2\left(\sqrt{14}+\sqrt{6}\right)=7+3\sqrt{14}+2\sqrt{6}\)

Lời giải:
i.

\(=\sqrt{(\sqrt{2}+1)^2}+|\sqrt{2}-2|=|\sqrt{2}+1|+|\sqrt{2}-2|=\sqrt{2}+1+2-\sqrt{2}=3\)

k.

\(=\frac{1}{\sqrt{2}}(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}+\sqrt{12})\)

\(=\frac{1}{\sqrt{2}}(\sqrt{(\sqrt{3}-\sqrt{5})^2}-\sqrt{(\sqrt{3}+\sqrt{5})^2}+2\sqrt{3})\)

\(=\frac{1}{\sqrt{2}}(|\sqrt{3}-\sqrt{5}|-|\sqrt{3}+\sqrt{5}|+2\sqrt{3})=\frac{1}{\sqrt{2}}(-2\sqrt{3}+2\sqrt{3})=0\)

m.

\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}-\frac{8\sqrt{2}(\sqrt{3}+\sqrt{7})}{(\sqrt{3}-\sqrt{7})(\sqrt{3}+\sqrt{7})}\)

\(=\sqrt{14}+7-\frac{8(\sqrt{14}+\sqrt{6})}{-4}=\sqrt{14}+\sqrt{7}+2(\sqrt{14}+\sqrt{6})=3\sqrt{14}+\sqrt{7}+2\sqrt{6}\)

bạn vẽ hình được không?

Bài 1: 

a) Xét ΔMNQ và ΔENQ có 

NM=NE(gt)

\(\widehat{MNQ}=\widehat{ENQ}\)

NQ chung

Do đó: ΔMNQ=ΔENQ(c-g-c)

Suy ra: QM=QE(hai cạnh tương ứng)

Bài 1: 

b) Ta có: ΔQMN=ΔQEN(cmt)

nên \(\widehat{QMN}=\widehat{QEN}\)(hai góc tương ứng)

mà \(\widehat{QMN}=90^0\)(gt)

nên \(\widehat{QEN}=90^0\)

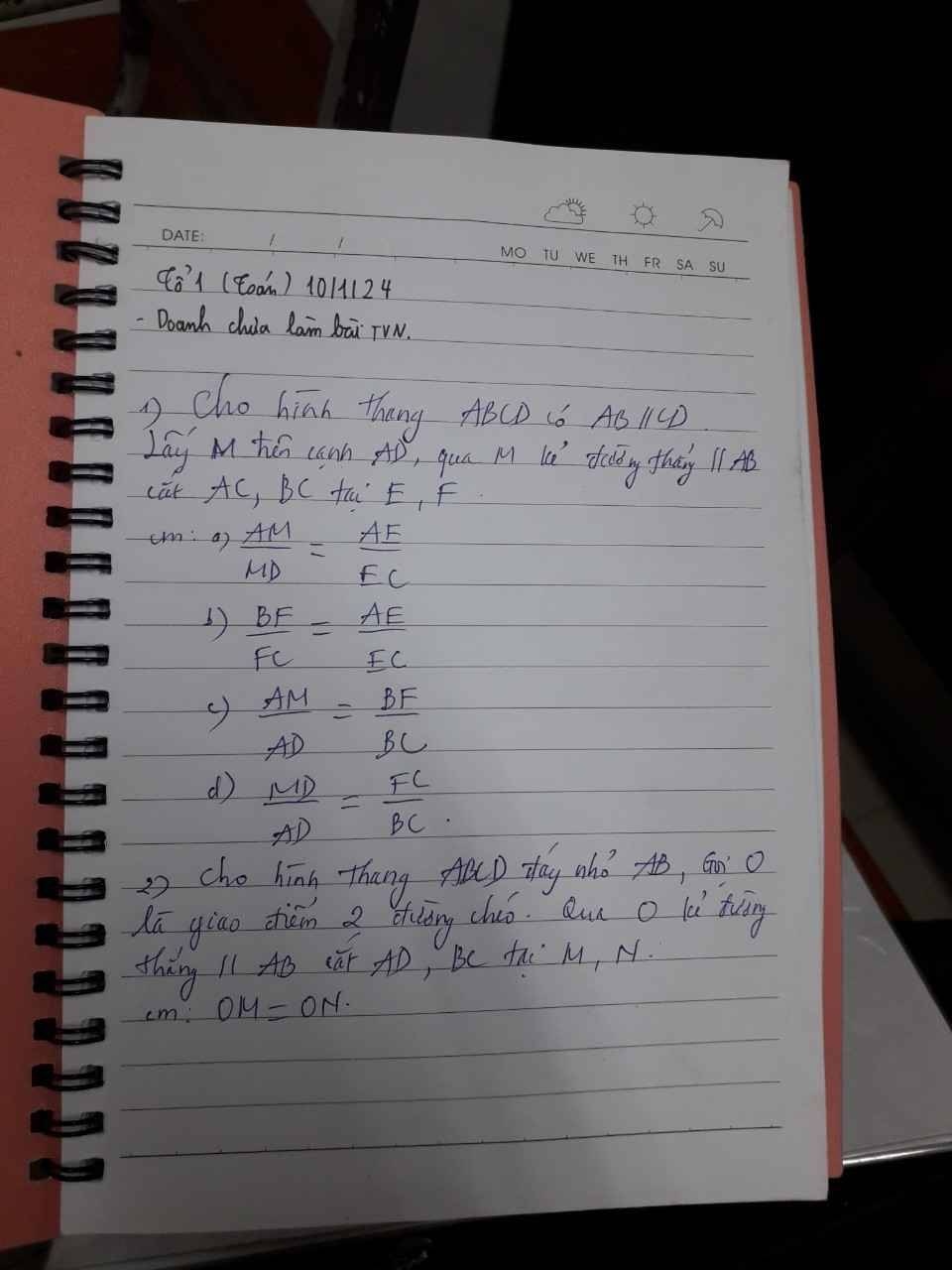
Câu 1:

a: Xét ΔADC có ME//DC

nên \(\dfrac{AM}{MD}=\dfrac{AE}{EC}\)

b: Xét ΔCAB có EF//AB

nên \(\dfrac{CE}{EA}=\dfrac{CF}{FB}\)

=>\(\dfrac{AE}{EC}=\dfrac{BF}{FC}\)

c: ta có: \(\dfrac{AM}{MD}=\dfrac{AE}{EC}\)

\(\dfrac{AE}{EC}=\dfrac{BF}{FC}\)

Do đó: \(\dfrac{AM}{MD}=\dfrac{BF}{FC}\)

d: Ta có: \(\dfrac{AM}{MD}=\dfrac{BF}{FC}\)

=>\(\dfrac{AM+MD}{MD}=\dfrac{BF+FC}{FC}\)

=>\(\dfrac{AD}{MD}=\dfrac{BC}{FC}\)

=>\(\dfrac{DM}{DA}=\dfrac{CF}{CB}\)

Bài 2:

Xét ΔADC có OM//DC

nên \(\dfrac{OM}{DC}=\dfrac{AM}{AD}\)(1)

Xét ΔBDC có ON//DC

nên \(\dfrac{ON}{DC}=\dfrac{BN}{BC}\left(2\right)\)

Xét hình thang ABCD có MN//AB//CD

nên \(\dfrac{AM}{MD}=\dfrac{BN}{NC}\)

=>\(\dfrac{MD}{AM}=\dfrac{CN}{BN}\)

=>\(\dfrac{MD+AM}{AM}=\dfrac{CN+BN}{BN}\)

=>\(\dfrac{AD}{AM}=\dfrac{BC}{BN}\)

=>\(\dfrac{AM}{AD}=\dfrac{BN}{BC}\left(3\right)\)

Từ (1),(2),(3) suy ra OM=ON