Tìm các số x,y biết rằng chúng thỏa mãn các đẳng thức sau:
x3+y3 = 152
x2 - xy + y2
x-y=2
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy =(1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P=1√1+x2 +1√1+y2 +4xy−x2−y2
Không nhìn thấy bất cứ chữ nào của đề bài cả
Chứng minh các bất đẳng thức sau với x, y, z > 0
a) x2 + y2 ≥ (x + y)2/2
b) x3 + y3 ≥ (x + y)3/4
c) x4 + y4 ≥ (x + y)4/8
d) x2 + y2 + z2 ≥ xy + yz + zx
e) x2 + y2 + z2 ≥ (x + y + z)2/3
f) x3 + y3 + z3 ≥ 3xyz
a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)
tìm các số x y biết rằng chúng thỏa mãn các đẳng thức sau:
a> x^3 + y^3 = 152 ; x^2 - xy +y^2=19 ; x-y =2
b> x+y = 2 ; x^2+y^2=20 tính x^3+y^3
1.Cho các số thực x, y thỏa mãn x+y+4=0. Tìm GTLN của biểu thức: A= 2(x3+y3)+3(x2+y2)+10xy
Cho x, y là các số thực thỏa mãn điều kiện 3 x 2 + y 2 - 2 . log 2 x - y = 1 2 1 + log 2 1 - x y . Tìm giá trị lớn nhất của biểu thức M = 2(x3 + y3) – xy.
A. 7
B. 13 2
C. 17 2
D. 3
Cho x , y là các số thực thỏa mãn điều kiện: 3 x 2 + y 2 - 2 . log 2 x - y = 1 2 [ 1 + log 2 ( 1 - x y ) ] . Tìm giá trị lớn nhất của biểu thức M = 2 ( x 3 + y 3 ) - 3 x y .
A. 3
B. 7
C. 17 2
D. 13 2
Tìm các số nguyênc: x, y thỏa mãn đẳng thức |(x-y)2 +2(xy+y2-4y)|=xy+y2-4y
Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$
Cho x,y là hai số thực thỏa mãn điều kiện x 2 + y 2 + x y + 4 = 4 y + 3 x . Tìm giá trị lớn nhất của biểu thức P = 3 ( x 3 - y 3 ) + 20 x 2 + 2 x y + 5 y 2 + 39 x .
![]()
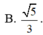
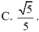
![]()
1,Viết dưới dạng bình phương của một đa thức bậc hai
A=x^4+2x^3+7x^2+6x+9
2,Tìm các số x,y biết chúng thỏa mãn các đẳng thức
x^3+y^3=152 x^2-xy+y^2=19 x-y=2
\(A=x^4+2x^3+7x^2+6x+9\)
\(=\left(x^2\right)^2+2.x^2.x+x^2+6\left(x^2+x\right)+9\)
\(=\left(x^2+x\right)^2+2.\left(x^2+x\right).3+3^2\)
\(=\left(x^2+x+3\right)^2\)
2, \(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(\Rightarrow152=\left(x+y\right).19\)
\(\Rightarrow x+y=8\)
Mà \(x-y=2\Rightarrow\hept{\begin{cases}x=\left(8+2\right):2=5\\y=x-2=3\end{cases}}\)
Vậy x = 5 và y = 3