ab=cd . Cmr a/b=ab+cd/b2 + d2

Những câu hỏi liên quan
a/b < c/d va b;d > 0 CMR : a/b < ab+cd/b2+d2 < c/d
a/b < c/d va b;d > 0 CMR : a/b < ab+cd/b2+d2 < c/d
ai nhanh mình tick
bn tham khảo câu hỏi tươg tự nhé
Đúng 0
Bình luận (0)
cho a/b<c/d(b;d>0) cmr a/b<ab+cd/b2+d2<c/d giải giúp mình mình sắp đi hoc rồi
Câu 5 (1đ): Cho a, b, c thỏa mãn a/b = c/d.Chứng minh rằng:a2 + b2/ c2+d2= ab/cd
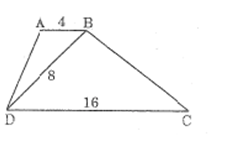
Hình thang ABCD (AB//CD) có : AB = 4cm , CD = 16cm , BD = 8cm
a) So sánh D2 và C
b) CMR: Sabd / Sbdc = 1/4
b: Xet ΔABD và ΔBDC có
AB/BD=BD/DC
góc ABD=góc BDC
=>ΔABD đồng dạng với ΔBDC
=>\(\dfrac{S_{ABD}}{S_{BDC}}=\left(\dfrac{AB}{BD}\right)^2=\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
Cho cac so duong abcd a+b+c+d =4.cm1/ab+1/cd+1/bc+1/da lon hon hoac bang a2+b2+c2+d2
Bài 3 Cho a2+b2 = c2+d2 = 1 và ac+bd = 0. Chứng minh rằng ab+cd = 0
\(ac+bd=0\)
\(=\) \(abc^2+abd^2+cda^2+cdb^2\)
\(=\) \(ac\left(bc+ad\right)+bd\left(ad+bc\right)\)
\(=\) \(\left(bc+ad\right)\left(ac+bd\right)=0\) \([\) vì ac+bd = 0 \(]\)
Đúng 2
Bình luận (0)
phân tích các đa thức sau thành nhân tử bằng phương pháp dùng hằng đẳng thức:
a) ( 4x^2 -3x -18 )^2 - ( 4x^2 +3x)^2
b) [ 4abcd +( a2+ b2) ( c2 +d2) ]2 -4[ cd (a2 + b2) +ab (c2 + d2)]2
cho a,b,c,d là các số tự nhiên thỏa mãn : đôi 1 khác nhau và a2+d2=b2+c2=t.
chứng minh ab+cd và ac+bd không thể đồng thời là số nguyên tố
Lời giải:
Ta thấy:
$(ab+cd)(ac+bd)=ad(c^2+b^2)+bc(a^2+d^2)$
$=(ad+bc)t$
Mà:
$2(t-ab-cd)=(a-b)^2+(c-d)^2>0$ nên $t> ab+cd$
Tương tự: $t> ac+bd$
Kết hợp $(ab+cd)(ac+bd)=(ad+bc)t$ nên:
$ab+cd> ad+bc, ac+bd> ad+bc$
Nếu $ab+cd, ac+bd$ đều thuộc $P$. Do $ad+bc$ là ước của $ab+cd$ hoặc $ac+bd$. Điều này vô lý
Do đó ta có đpcm.
Đúng 1
Bình luận (0)
Chứng minh rằng x2 - 12x + 37 > 0
Cho a2 + b2 = 1 , c2+ d2 = 1
, ab + bc = 0
CMR : ab + cd = 0
heo miiiiii ~~~
Lớp 6 nên chưa pít nhìu :v
\(x^2-12x+37\)
\(=x^2-6x-6x+36+1\)
\(=x\left(x-6\right)-6\left(x-6\right)+1\)
\(=\left(x-6\right)\left(x-6\right)+1\)
\(=\left(x-6\right)^2+1\)
\(\left(x-6\right)^2\ge0\)
\(\Rightarrow\left(x-6\right)^2+1>0\rightarrowđpcm\)
Đúng 0
Bình luận (0)