b: Xet ΔABD và ΔBDC có
AB/BD=BD/DC
góc ABD=góc BDC
=>ΔABD đồng dạng với ΔBDC
=>\(\dfrac{S_{ABD}}{S_{BDC}}=\left(\dfrac{AB}{BD}\right)^2=\dfrac{1}{4}\)
cho hình thang ABCD (AB//CD) có: AB=4cm;BD=6cm;CD=9cm.Gọi I là giao điểm của AC và BD hỏi:
Tính SABCD biết SABD= 16cm vuông
Hình thang ABCD (AB // CD) có AB= 4cm, CD = 16cm và BD = 8cm. Chứng minh: ∠ (BAD) = ∠ (DBC) và BC =2AD.
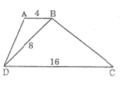
Hình thang ABCD (AB//CD) có AB = 4cm; CD = 16cm và BD = 8cm, góc ADB bằng 40 độ . Tính số đo góc C của hình thang.
Cho hình thang ABCD có AB//CD,AB=4cm,CD=16cm,BD=8cm. Cm góc BAD= góc DBC và BC=2 lần AD
Cho hình thang ABCD (AB // CD) có: AB=4cm , CD=16cm ,BD=8cm ,\(\widehat{ADB}\)= 40độ.Tính góc C trong hình thang
a. Cho Tam giác ABC vuông tại A, từ điểm H trên cạnh AC kẻ HK ^ BC tại K. Chứng minh: AB. KC = KH. AC.
b. Cho hình thang ABCD (AB//CD, AB < CD) có AB = 4cm, CD = 16cm, BD = 8cm. Chứng minh: góc DAB và góc DBC.
c. Cho ∆ABC nhọn , hai đường cao AH và BK cắt nhau tại I. Chứng minh: CA.BK = AH.BC.
Cho hìn thang ABCD ( AB // CD ) có: AB =4cm, CD= 16cm, BD=8cm. C/m \(\widehat{BAD}=\widehat{DBC}\); BC=2AD
Cho hình thang ABCD (AB//CD) có AB =2cm; BD = 4cm; CD = 8cm. Chứng minh rằng A ˆ = DB ˆ C
Cho hình thang cân ABCD (AB//CD) có AC vuông góc với BD tại O. Biết AB=4cm, CD=8cm. Tính diện tích hình thang ABCD.
