Trên hệ trục tọa độ Oxy cho 2 điểm A(0; 1) và B(1; -2). Tìm H\(\in\)Ox sao cho |HA-HD| đạt giá trị lớn nhất.

Những câu hỏi liên quan
trong hệ tọa độ Oxy , cho 2 điểm A( 2;2 ) và B( 1;5 ) . tìm tọa độ điểm M trên trục tung sao cho độ dài MA + MB nhỏ nhất
vẽ hệ trục tọa độ Oxy và đánh dấu các điểm A(3;\(\frac{-1}{2}\)), B(-2;1), C(0;-3), D(2;0) trên hệ trục
Biết rằng cả ba số a,b,c đều khác 0. Trong hệ trục tọa độ (Oxyz), tọa độ điểm M nằm trên mặt phẳng (Oxy) nhưng không nằm trên trục Ox và Oy có thể là
Đọc tiếp
Biết rằng cả ba số a,b,c đều khác 0. Trong hệ trục tọa độ (Oxyz), tọa độ điểm M nằm trên mặt phẳng (Oxy) nhưng không nằm trên trục Ox và Oy có thể là
![]()
![]()
![]()
![]()
Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 điểm A91;2) và B(4;3). Tìm tọa độ điểm M trên trục hoành sao cho góc AMB bằng 45 độ.
Giả sử tọa độ M(x;0). Khi đó \(\overrightarrow{MA}=\left(1-x;2\right);\overrightarrow{MB}=\left(4-x;3\right)\)
Theo giả thiết ta có \(\overrightarrow{MA}.\overrightarrow{MB}=MA.MB.\cos45^0\)
\(\Leftrightarrow\left(1-x\right)\left(4-x\right)+6=\sqrt{\left(1-x\right)^2+4}.\sqrt{\left(4-x\right)^2+9}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow x^2-5x+10=\sqrt{x^2-2x+5}.\sqrt{x^2-8x+25}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow2\left(x^2-5x+10\right)^2=\left(x^2-5x+10\right)\left(x^2-8x+25\right)\) (do \(x^2-5x+10>0\))
\(\Leftrightarrow x^4-10x^3+44x^2-110x+75=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)\left(x^2-4x+15\right)=0\)
\(\Leftrightarrow x=1;x=5\)
Vậy ta có 2 điểm cần tìm là M(1;0) hoặc M(5;0)
Đúng 2
Bình luận (0)
Trong mp với hệ tọa đô Oxy cho hai điểm A(1;-2), B(-4;5). Tìm tọa độ điểm M trên trục Oy sao cho 3 điểm M,A,B thẳng hàng
Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
Đúng 2
Bình luận (0)
Trên hệ trục tọa độ Oxy với đơn vị trên 2 trục bằng nhau cho các điểm A(1;5), B(3;1), C(-3;-3).
1) vẽ hệ trục tọa độ Oxy và các điểm A, B,C
2) viết phương trình đường thẳng OA
3) tính diện tích tam giác ABC nếu biết đơn vị trên các trục là 1cm.
mọi người giúp mik với, mik đang cần gấp.........
trong mp tọa độ oxy cho 2 điểm A(-1;4),B(0;-2) tìm tọa độ điểm D trên trục ox sao cho tam giác ABD cân tại D
Xem chi tiết
D thuộc trục Ox nên D(x;0)
\(DA=\sqrt{\left(-1-x\right)^2+\left(4-0\right)^2}=\sqrt{\left(x+1\right)^2+16}\)
\(DB=\sqrt{\left(0-x\right)^2+\left(-2-0\right)^2}=\sqrt{x^2+4}\)
Để ΔDAB cân tại D thì DA=DB
=>\(\left(x+1\right)^2+16=x^2+4\)
=>\(x^2+2x+1+16=x^2+4\)
=>2x+17=4
=>2x=4-17=-13
=>\(x=-\dfrac{13}{2}\)
Vậy: \(D\left(-\dfrac{13}{2};0\right)\)
Đúng 1
Bình luận (0)
Bài 1: Cho (d1): y = 3x + 2 (d2): y = x – 2 a) Tìm tọa độ giao điểm của (d1) và (d2) với trục hoành b) Tìm tọa độ giao điểm của (d1) và (d2) với trục tung c) Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy d) Tìm tọa độ giao điểm của (d1) và (d2)
\(b,\) PT hoành độ giao điểm: \(3x+2=x-2\Leftrightarrow x=-2\Leftrightarrow y=-4\Leftrightarrow A\left(-2;-4\right)\)
Vậy \(A\left(-2;-4\right)\) là tọa độ giao điểm
Đúng 1
Bình luận (0)
Vẽ một hệ trục tọa độ Oxy với đơn vị trên hai trục bằng nhau và biểu diễn các điểm trên hệ trục tọa độ đó.
Xem chi tiết
A(-3;2); B(4;-1); C(3;2); D(-2;-1)
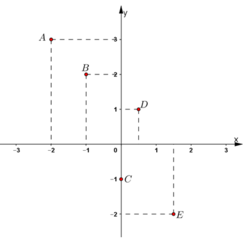
Hàm số y f(x) được cho bằng bảng sau :
x
-2
-1
0
0,5
1,5
y
3
2
-1
1
-2
Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm có tọa độ là các cặp số trên
Đọc tiếp
Hàm số y = f(x) được cho bằng bảng sau :
| x | -2 | -1 | 0 | 0,5 | 1,5 |
| y | 3 | 2 | -1 | 1 | -2 |
Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm có tọa độ là các cặp số trên