Giúp mik mấy bài này vs mik cần gấp
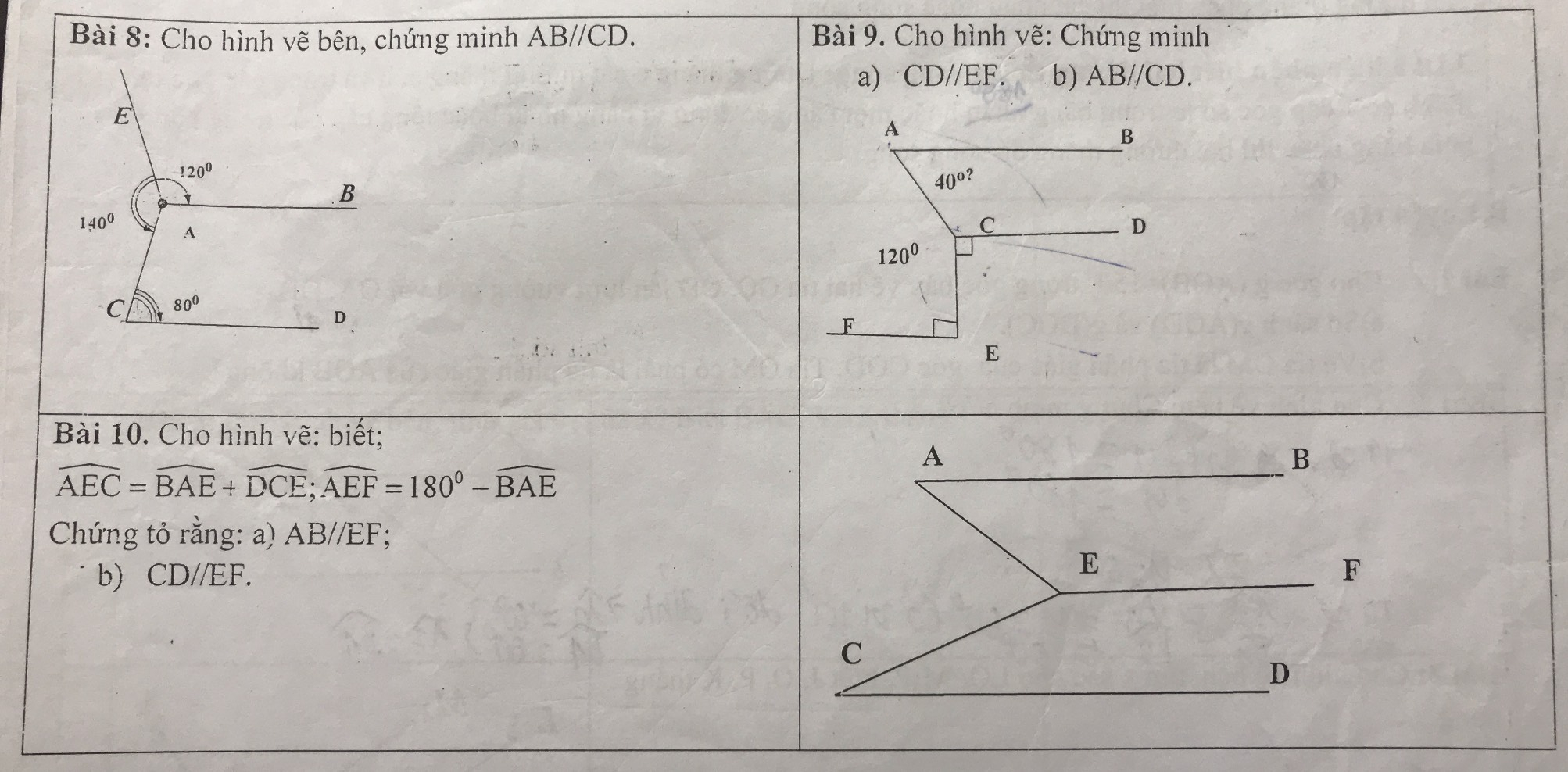
Giúp mấy bài này vs mik cần gấp .
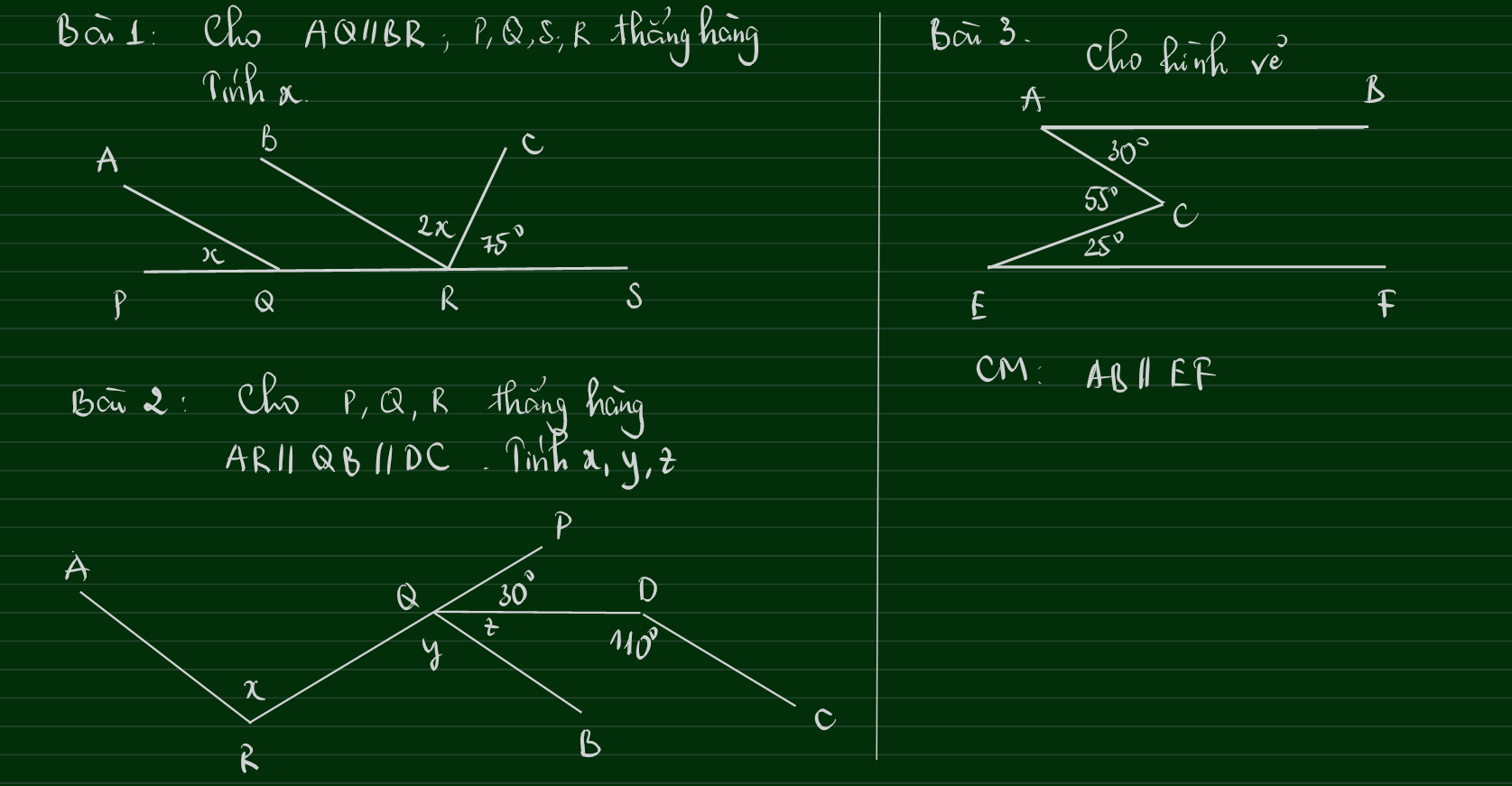
Bài 1:
Vì $AQ\parallel BR$ nên $\widehat{PQA}=\widehat{QRB}$ (hai góc đồng vị )
$\Rightarrow \widehat{QRB}=x$
Lại có:
$Q,R,S$ thẳng hàng nên
$\widehat{QRS}=180^0$
$\widehat{QRB}+\widehat{BRC}+\widehat{CRS}=180^0$
$x+2x+75^0=180^0$
$3x+75^0=180^0$
$x=35^0$
Bài 2:
Vì $QB\parallel DC$ nên: $\widehat{BQD}+\widehat{QDC}=180^0$ (hai góc trong cùng phía)
$z+110^0=180^0$
$z=70^0$
$P,Q,R$ thẳng hàng
$\Rightarrow \widehat{PQR}=180^0$
$\widehat{RQB}+\widehat{BQD}+\widehat{DQP}=180^0$
$y+z+30^0=180^0$
$y+70^0+30^0=180^0$
$y=80^0$
$AR\parallel QB$
$\Rightarrow x=y=80^0$ (hai góc so le trong)
Mấy bn ơi ,Mấy bn giải giup mik bài này vs càng nhanh càng tốt nha mai mik nộp cho cô r
DTXQ hình lập phương:9,6dm vuông
DTTP:?dm vuông các bn giúp cho mik vs mik cần gấp
đề bài cs sai ko bn ơi sao mink ko tách đc
Giúp mik bài này vs ạ mik đang cần gấp
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)

giúp mik giải bài này vs![]()
![]() mik đag cần gấp
mik đag cần gấp
1: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
2: Xét ΔFBH vuông tại F và ΔFAC vuông tại F có
\(\widehat{FBH}=\widehat{FAC}\left(=90^0-\widehat{ACF}\right)\)
Do đó: ΔFBH~ΔFAC
=>\(\dfrac{FB}{FA}=\dfrac{FH}{FC}\)
=>\(FB\cdot FC=FA\cdot FH\)
3: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
nên AEHD là tứ giác nội tiếp đường tròn đường kính AH
Tâm I là trung điểm của AH

giúp mik giải bài này vs![]() mik đag cần gấp
mik đag cần gấp
a.
Do MA là tiếp tuyến tại A \(\Rightarrow MA\perp OA\Rightarrow\widehat{MAO}=90^0\)
Xét hai tam giác OMA và OMB có:
\(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\\OM\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OMA=\Delta OMB\left(c.c.c\right)\)
\(\Rightarrow\widehat{MBO}=\widehat{MAO}=90^0\)
\(\Rightarrow MB\perp OB\Rightarrow MB\) là tiếp tuyến
b.
Gọi H là giao điểm AB và OM
Ta có: \(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow OM\) là trung trực AB
\(\Rightarrow OM\perp AB\) tại H đồng thời \(HA=HB=\dfrac{AB}{2}\)
Trong tam giác vuông OMA: \(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AMO}=90^0-\widehat{AOM}=30^0\)
\(\Rightarrow\widehat{AMB}=2\widehat{AMO}=60^0\)
\(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
Trong tam giác vuông OAH:
\(AH=OA.sin\widehat{AOM}=R.sin60^0=\dfrac{R\sqrt{3}}{3}\)
\(\Rightarrow AB=2AH=R\sqrt{3}\)
\(OH=OA.cos\widehat{AOM}=R.cos30^0=\dfrac{R}{2}\)
\(\Rightarrow HM=OM-OH=\dfrac{3R}{2}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}HM.AB=\dfrac{3R^2\sqrt{3}}{4}\)
c.
BE là đường kính \(\Rightarrow\widehat{BAE}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAE}=90^0\Rightarrow AB\perp AE\)
Mà \(AB\perp OM\) (theo cm câu b)
\(\Rightarrow AE||OM\) (cùng vuông góc AB)
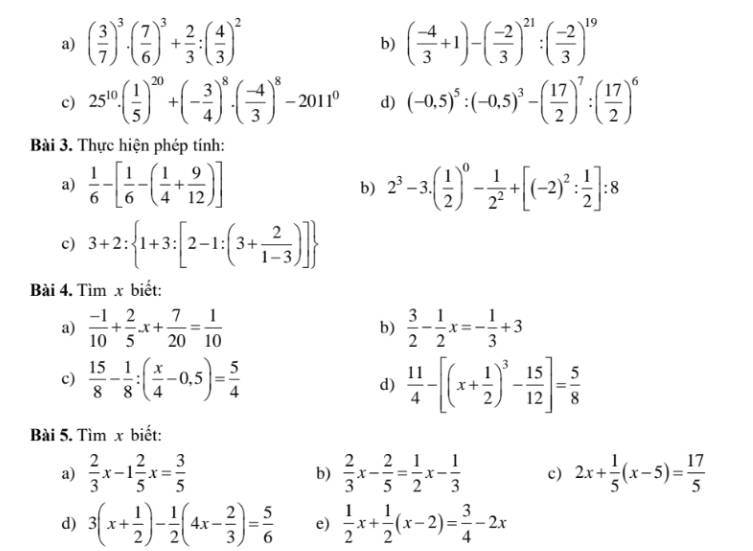
giúp mik mấy bài này với ạ mik đg cần gấp ạ
4:
a: =>2/5x+7/20-2/20=1/10
=>2/5x+5/20=1/10
=>2/5x=1/10-1/4=4/40-10/40=-6/40=-3/20
=>x=-3/20:2/5=-3/20*5/2=-15/40=-3/8
b: 3/2-1/2x=-1/3+3=8/3
=>1/2x=3/2-8/3=9/6-16/6=-7/6
=>x=-7/6*2=-7/3
c: 15/8-1/8:(1/4x-0,5)=5/4
=>1/8:(1/4x-1/2)=15/8-5/4=15/8-10/8=5/8
=>1/4x-1/2=1/8:5/8=1/5
=>1/4x=1/5+1/2=7/10
=>x=7/10*4=28/10=2,8
d: \(\Leftrightarrow\left[\left(x+\dfrac{1}{2}\right)^3-\dfrac{5}{4}\right]=\dfrac{11}{4}-\dfrac{5}{8}=\dfrac{22-5}{8}=\dfrac{17}{8}\)
=>\(\left(x+\dfrac{1}{2}\right)^3=\dfrac{17}{8}+\dfrac{5}{4}=\dfrac{27}{8}\)
=>x+1/2=3/2
=>x=1
Mn ơi giúp mik giải bài này vs mik cần gấp ạ >
Giúp mik giả bài này vs, mik đang cần gấp. Giải chi tiếc giùm mik nha.





giúp mik mấy bài này với mik cần rất gấp trước 3h nha