tìm số tự nhiên n để phép chia thực hiện được
a) x5 : xn
b) x2n : x5
c) 3x5yn : 2ny3
d) xn+2y3 : x5y3
e) x3n+1 : x7
f) xnyn+3 : x6y10
Thực hiện phép tính
(x2n+xnyn+y2n)(xn-yn)(x3n+y3n)
\(\left(x^{2n}+x^ny^n+y^{2n}\right)\left(x^n-y^n\right)\left(x^{3n}+y^{3n}\right)\\ =\left[\left(x^n\right)^2+x^ny^n+\left(y^n\right)^2\right]\left(x^n-y^n\right)\left(x^{3n}+y^{3n}\right)\\ =\left(x^{3n}-y^{3n}\right)\left(x^{3n}+y^{3n}\right)=x^{6n}-y^{6n}\)
Giá trị số tự nhiên n để phép chia x n : x 6 thực hiện được là:
A. n Є N, n < 6
B. n Є N, n ≥ 6
C. n Є N, n > 6
D. n Є N, n ≤ 6
Để phép chia x n : x 6 thực hiện được thì n Є N, n – 6 ≥ 0 ó n ≥ 6, n Є N
Đáp án cần chọn là: B
Tìm số tự nhiên n để đa thức:
A(x)=x2n+xn+1 chia hết cho đa thức x2+x+1.
Vì \(A\left(x\right)=x^{2n}+x^n+1\) chỉ có một hằng số là1
đa thức \(x^2+x+1\) cũng chỉ có một hằng số là 1
Để \(A\left(x\right)⋮x^2+x+1\) thì thì \(A\left(x\right)\) phải có số mũ tương ứng với các bậc như đa thức : => n=1
-Đáp án cuối cùng: \(n=3k+1\) hay \(n=3k+2\)



Tìm số tự nhiên n để đa thức:
A(x)=x2n+xn+1 chia hết cho đa thức x2+x+1.
Giá trị số tự nhiên n để phép chia x 2 n : x 4 thực hiện được là:
A. n Є N, n > 2
B. n Є N, n ≥ 4
C. n Є N, n ≥ 2
D. n Є N, n ≤ 2
Để phép chia x 2 n : x 4 thực hiện được thì n Є N, 2n – 4 ≥ 0 ó n ≥ 2, n Є N
Đáp án cần chọn là: C
F(x)=x5+ax4+bx3+cx2+dx+e .Biết f(1)=1 ;f(2)=4 ;f(3)=9 ;f(4)=16 ;f(5)=25 ; a)Tính f(6)? b)Tìm số tự nhiên n. Biết f(x) chia cho (x-n) dư 448767600049
Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết: x 4 : x n
x 4 : x n = x 4 - n là phép chia hết nên 4 – n ≥ 0 ⇒ 0 ≤ n ≤ 4
suy ra: n ∈ {0; 1; 2; 3; 4}
Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết: x n y n + 1 : x 2 y 5
x n y n + 1 : x 2 y 5 = x n : x 2 y n + 1 : y 5 = x n - 2 . y n - 4 là phép chia hết
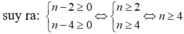
. Đơn thức -8x3 y2z3t3 chia hết cho đơn thức nào?
A. -2x3 y3z3t4.
B. -9x3 yz2t 2.
C. 4x4 y2zt2.
D. 2x3 y2z2t4.
Câu 132. Giá trị của số tự nhiên n để phép chia xn+3 y6 : x9 yn là phép chia hết?
A. n < 6.
B. n = 5.
C. n > 6.
D. n = 6.
Cho đa thức A(x) = 1 + x2 + x4 + .... + x2n - 2; B= 1 + x + x2 + ... + xn-1. Tìm số nguyên dương n để đa thức A(x) chia hết cho đa thức B(x).
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1