Bài 5: 

a: Xét tứ giác ABDC có 

M là trung điểm của BC

M là trung điểm của AD

Do đó: ABDC là hình bình hành

Suy ra: CD//AB và CD=AB

b: Ta có: ΔABC vuông tại A

mà AM là đường trung tuyến

nên AM=BC/2

my parents are enjoying their summer vacation in Miami

they are drinking coffee with friends

Look! it's starting to rain!

They are buying some cakes for the kids at home

What is your brother doing?

\(\left|2x-3\right|=3-2x\)

\(ĐK:x\le\dfrac{3}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)

Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)

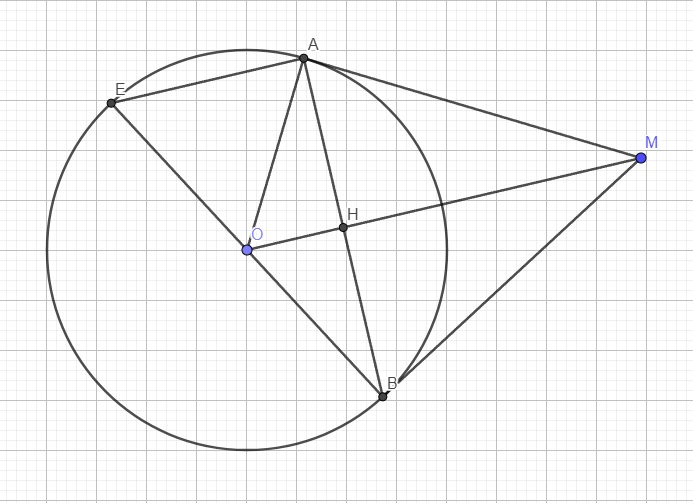
1: Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>CE\(\perp\)AB tại E

Xét (O) có

ΔBDC nội tiếp

BC là đường kính

Do đó: ΔBDC vuông tại D

=>BD\(\perp\)AC tại D

Xét ΔABC có

BD,CE là các đường cao

BD cắt CE tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC tại F

2: Xét ΔFBH vuông tại F và ΔFAC vuông tại F có

\(\widehat{FBH}=\widehat{FAC}\left(=90^0-\widehat{ACF}\right)\)

Do đó: ΔFBH~ΔFAC

=>\(\dfrac{FB}{FA}=\dfrac{FH}{FC}\)

=>\(FB\cdot FC=FA\cdot FH\)

3: Xét tứ giác AEHD có

\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)

nên AEHD là tứ giác nội tiếp đường tròn đường kính AH

Tâm I là trung điểm của AH

a.

Do MA là tiếp tuyến tại A \(\Rightarrow MA\perp OA\Rightarrow\widehat{MAO}=90^0\)

Xét hai tam giác OMA và OMB có:

\(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\\OM\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OMA=\Delta OMB\left(c.c.c\right)\)

\(\Rightarrow\widehat{MBO}=\widehat{MAO}=90^0\)

\(\Rightarrow MB\perp OB\Rightarrow MB\) là tiếp tuyến

b.

Gọi H là giao điểm AB và OM

Ta có: \(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow OM\) là trung trực AB

\(\Rightarrow OM\perp AB\) tại H  đồng thời \(HA=HB=\dfrac{AB}{2}\)

Trong tam giác vuông OMA: \(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)

\(\Rightarrow\widehat{AMO}=90^0-\widehat{AOM}=30^0\)

\(\Rightarrow\widehat{AMB}=2\widehat{AMO}=60^0\)

\(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)

Trong tam giác vuông OAH:

\(AH=OA.sin\widehat{AOM}=R.sin60^0=\dfrac{R\sqrt{3}}{3}\)

\(\Rightarrow AB=2AH=R\sqrt{3}\)

\(OH=OA.cos\widehat{AOM}=R.cos30^0=\dfrac{R}{2}\)

\(\Rightarrow HM=OM-OH=\dfrac{3R}{2}\)

\(\Rightarrow S_{ABM}=\dfrac{1}{2}HM.AB=\dfrac{3R^2\sqrt{3}}{4}\)

c.

BE là đường kính \(\Rightarrow\widehat{BAE}\) là góc nt chắn nửa đường tròn

\(\Rightarrow\widehat{BAE}=90^0\Rightarrow AB\perp AE\)

Mà \(AB\perp OM\) (theo cm câu b)

\(\Rightarrow AE||OM\) (cùng vuông góc AB)

\(0,5x-\frac{2}{3}x=\frac{5}{12}\)

\(\frac{1}{2}x-\frac{2}{3}x=\frac{5}{12}\)

\(x.\left(\frac{1}{2}-\frac{2}{3}\right)=\frac{5}{12}\)

\(\Rightarrow x=-\frac{5}{2}\)

đúng chứ bn 

-Ta nhận biết được ánh sáng khi có ánh sáng truyền vào mắt

 ta. Ta nhìn thấy một vật khi có ánh sáng từ vật đó truyền vào mắt ta

Câu 2

-Định luật truyền thẳng ánh sáng: trong môi trường trong suốt và đồng tính ánh sáng truyền đi theo đường thẳng

-Định luật phản xạ ánh sáng:

+Tia phản xạ nằm trong mặt phẳng chứa tia tới và pháp tuyến của gương ở điểm tới

+Góc phản xạ bằng góc tới

-Có thể ứng dụng để trồng cây, học sinh xếp hàng, giải thích hiện tượng nhật thực nguyệt thực,...

bạn có thể tìm trong sách giáo khoa Vật Lý nha 

Câu nào bạn

C

a: Xét ΔABE vuông tại B và ΔADE vuông tại D có 

AE chung

\(\widehat{BAE}=\widehat{DAE}\)

Do đó: ΔABE=ΔADE

b: Ta có: ΔABE=ΔADE

nên AB=AD và EB=ED

Ta có: AB=AD

nên A nằm trên đường trung trực của BD\(\left(1\right)\)

Ta có: EB=ED

nên E nằm trên đường trung trực của BD\(\left(2\right)\)

Từ \(\left(1\right),\left(2\right)\) suy ra AE là đường trung trực của BD