Cho tam giác ABC có AB=1,\(\widehat{A}=105o;\widehat{B}=60o\)BE=1(E thuộc BC).Qua E kẻ ED//BC(D thuộc AC)
CMR:\(\dfrac{1}{AC^2}+\dfrac{1}{AD^2}=\dfrac{4}{3}\)
Cho tam giác ABC có BC = 2 cm, góc A=105o , góc C=30o. Tính diện tích tam giác ABC.
Ta có :
góc C = 180o - 105o - 30o = 45o
Kẻ đường cao AH
Gọi BH = x(cm) $\to$ CH = 2 - x(cm)
Trong tam giác AHB vuông tại H và tam giác AHC vuông tại H, ta có :
\(AH=BH.tanB=x.tan45^o=x\\ AH=CH.tanC=\left(2-x\right).tan30^o=\dfrac{\sqrt{3}}{3}\left(2-x\right)\)
Suy ra :
\(x=\dfrac{\sqrt{3}}{3}\left(2-x\right)\Leftrightarrow x=\dfrac{2\sqrt{3}}{3+\sqrt{3}}\)
Suy ra:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2\sqrt{3}}{3+\sqrt{3}}.2\simeq0,732\left(cm^2\right)\)
Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
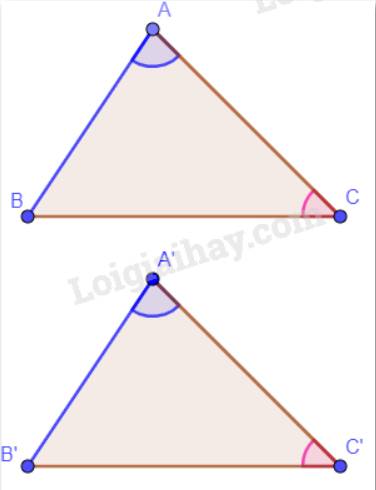
Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).
Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Cho tam giác ABC có \(\widehat{C}=2\widehat{B}=4\widehat{A}\). CMR: \(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{1}{BC}\)
Cho tam giác ABC có Aˆ=60o,Bˆ=105o. So sánh độ dài ba cạnh của △ABC
1.Cho tam giác ABC có AB = 6cm; BC = 9cm. So sánh \(\widehat{A}\)và\(\widehat{C}\).
2.Cho tam giác ABC có tia phân giác AD. So sánh AC và DC.
1 . Xét tam giác \(ABC\):
Ta thấy cạnh \(AB\)đối với góc \(C\), cạnh \(BC\)đối với góc \(A\).
Do \(BC>AB\)mà \(9>6\)nên ta kết luận rằng \(A>C\)
2 .
Xét tam giác \(ABC\), ta thấy \(AD\)đối nhau với cạnh \(AC\)
Mà \(DC\)thuộc đường thẳng \(AD\)nên ta kết luận \(AC>DC\)
TL
1.Cho tam giác ABC có AB = 6cm; BC = 9cm.
=>\(\widehat{A}\)> \(\widehat{C}\)(quan hệ giữa cạnh và góc trong tam giác)
TL
mình nghĩ là AC>DC
Ko bt nói sao nữa
:((
Cho tam giác ABC có góc A = 75 độ, AB = 10,6 cm, \(\widehat{B}\) : \(\widehat{C}\) = 4:3. Tính CA, CB và diện tích tam giác ABC
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
Cho tam giác \(DEF\) và tam giác \(ABC\) có \(DE = \frac{1}{3}AB,DF = \frac{1}{3}AC,\widehat D = \widehat A\) (Hình 5). Trên tia \(AB\), lấy điểm \(M\) sao cho \(AM = DE\). Qua \(M\) kẻ \(MN//BC\left( {N \in AC} \right)\).
a) So sánh \(\frac{{AM}}{{AB}}\) và \(\frac{{AN}}{{AC}}\)
b) So sánh \(AN\) với \(DF\).
c) Tam giác \(AMN\) có đồng dạng với tam giác \(ABC\) không?
d) Dự đoán sự đồng dạng của hai tam giác \(DEF\) và \(ABC\).
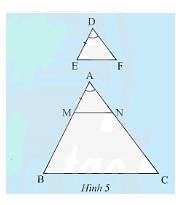
a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).
b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).
Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
d) Dự đoán hai tam giác \(DEF\) và \(ABC\) đồng dạng.
Bài 1.Tam giác ABC vuông tại A, có AB = 21cm, \(\widehat{C}\) = 40°, phân giác BD của góc ABC, D ∈ AC. Tính
a) độ dài đoạn thẳng AC, BC
b) độ dài đoạn thẳng BD
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính \(\widehat{B},\) \(\widehat{C}\)
Bài 3. Cho tam giác ABC vuông tại A có \(\widehat{B}\) = 30 °, AB = 6cm
a) Giải tam giác vuông ABC
b) Vẽ đường cao AH và trung tuyến Am của tam giác ABC. Tính diện tích tam giác AHM
Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)
Cho hai tam giác ABC và A’B’C’ (Hình 57) có: \(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
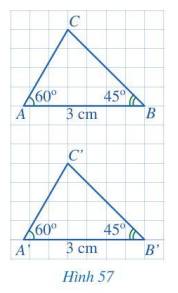
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)