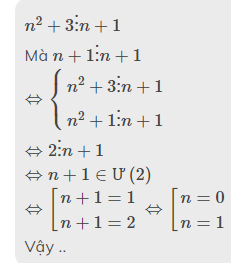tìm số nguyên n sao cho n2+2n-4 chia hết cho 11

Những câu hỏi liên quan
tìm số nguyên n sao cho :
1,n^2+2n-4 chia hết cho 11
2,2n^3+n^2+7n+1 chia hết cho 2n -1
3,n^4-2n^3+2n^2-2n+1 chia hết cho n^4-1
: Tìm n є N sao cho:
a/ n + 6 chia hết cho n + 2
b/ 2n + 3 chia hết cho n – 2
c/ 3n + 1 chia hết cho 11 – 2n
d/ n2 + 4 chia hết cho n + 1
cách khác : a/ n + 6 = (n + 2) + 4 chia het cho n + 2 => 4 chia het cho n + 2 => n + 2 la uoc cua 4
=>ma n + 2 >=2 nen ta co hai truong hop
n + 2 = 4 => n = 2;
n + 2 = 2 => n = 0,
Vay n = 2 ; 0.
b/ Tuong tu cau a
c/ (3n + 1) Chia het cho 11 - 2n => [2(3n + 1) + 3(11 - 2n)] chia het cho 11 - 2n
=> 35 chia het cho 11 - 2n =>
+)11 - 2n = 1 => n = 5
+)11 - 2n = 5 => n = 3
+)11 - 2n = 7 => n = 2
+)11 - 2n = 35 => n < 0 (loai)
+)11 - 2n = -1 => n = 6
+)11 - 2n = - 5 => n = 8
+)11 - 2n = -7 => n = 9
+)11 - 2n = -35 => n=23
Vay : n = 2;3;5;6;8;9;23
d/ B = (n2 + 4):(n + 1) = [(n +1)(n - 1) + 5]:(n + 1) = n - 1 + 5/(n +1)
Do n2 + 4 chia het cho n + 1 => 5 chia het cho n +1 => n = 0;4.
Đúng 0
Bình luận (0)
a) n+6 chia hết cho n+2=> n+2 là ước của n+6=>n+2 là Ư(4)={-4,-2,-1,1,2,4}
n+2=-4=>n=-6
n+2=-2=>n=-4
n+2=-1=>n=-3
n+2=1=>n=-1
n+2=2=>n=0
n+2=4=>n=2
vậy x thuộc {-6,-4,-3,-1,0,2}
b) tương tự
Đúng 0
Bình luận (0)
a) n + 4 chia hết cho n
vì n chia hết cho n =>để n + 4 chia hết cho n thì 4 phải chia hết cho n
=>n Є {1;2;4}
b/ 3n + 7 chia hết cho n
vì 3n chia hết cho n => để 3n + 7 chia hết cho n thì 7 phải chia hết cho n
=>n Є {1;7}
c) 27 - 5n chia hết cho n
vì 5n chia hêt cho n => để 27 - 5n chia hết cho n thì 27 phải chia hết cho n
=>n Є {1;3; 9;27}
d) n+6 chia hết cho n + 2
ta có n+6= (n+2) +4
vì n+2 chia hết cho n+2 =>để (n+2) +4 chia hết cho n + 2 thì 4 phải chia hết cho n+2
=>(n+2) Є {2;4} (vì n+2 >=2)
=>n Є {0;2}
e) 2n + 3 chia hết cho n + 2 - 2 hay 2n + 3 chia hết cho n
vì 2n chia hết cho n =>để 2n + 3 chia hết cho n thì 3 phải chia hêt cho n
=>n Є {1;3}
f) 3n + 1 chia hết cho 11 - 2n
để 11 -2n >=0 => n Є {0;1;2;3;4;5}
mặt khác để 3n + 1 chia hết cho 11 - 2n thì
3n+1 >= 11-2n =>5n - 2n+1 >=10-2n +1
=>5n >= 10 =>n>=2 => n Є {2;3;4;5}
* với n=2 => 3n+1=7 ; 11-2n=7 =>3n+1 chia hết cho 11-2n vậy n=2 thỏa mãn
*với n=3 => 3n+1=10; 11-2n=5 =>3n+1 chia hết cho 11-2n vậy n=3 thỏa mãn
* với n=4 =>3n+1=13; 11-2n=3 =>3n+1 không chia hết cho 11-2n vậy n=4 không thỏa mãn
*với n=5 =>3n+1=16; 11-2n=1 =>3n+1 chia hết cho 11-2n vậy n=5 thỏa mãn
vậy n Є {2;3;5}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm n є N sao cho:
a/ n + 6 chia hết cho n + 2
b/ 2n + 3 chia hết cho n – 2
c/ 3n + 1 chia hết cho 11 – 2n
d/ n2 + 4 chia hết cho n + 1
a. n + 6 chia hết cho n + 2
=> n + 2 + 4 chia hết cho n + 2
Mà n + 2 chia hết cho n + 2
=> 4 chia hết cho n + 2
=> n + 2 thuộc Ư(4) = {-4; -2; -1; 1; 2; 4}
Mà n thuộc N
=> n thuộc {0; 2}.
b. 2n + 3 chia hết cho n - 2
=> 2n - 4 + 7 chia hết cho n - 2
=> 2.(n - 2) + 7 chia hết cho n - 2
Mà 2.(n - 2) chia hết cho n - 2
=> 7 chia hết cho n - 2
=> n - 2 thuộc Ư(7) = {-7; -1; 1; 7}
Mà n thuộc N
=> n thuộc {1; 3; 9}.
c. 3n + 1 chia hết cho 11 - 2n
=> 3n + 1 chia hết cho -(11 - 2n)
=> 3n + 1 chia hết cho 2n - 11
=> 2.(3n + 1) chia hết cho 2n - 11
=> 6n + 2 chia hết cho 2n - 11
=> 6n - 33 + 35 chia hết cho 2n - 11
=> 3.(2n - 11) + 35 chia hết cho 2n - 11
=> 35 chia hết cho 2n - 11
=> 2n - 11 thuộc Ư(35) = {-35; -7; -5; -1; 1; 5; 7; 35}
Mà n thuộc N
=> n thuộc {2; 3; 5; 6; 8; 9; 23}
d. n2 + 4 chia hết cho n + 1
=> n2 + 4 - n.(n + 1) chia hết cho n + 1
=> n2 + 4 - n2 - n chia hết cho n + 1
=> -n + 4 chia hết cho n + 1
=> -(n - 4) chia hết cho n + 1
=> n - 4 chia hết cho n + 1
=> n + 1 - 5 chia hết cho n + 1
=> 5 chia hết cho n + 1
=> n + 1 thuộc Ư(5) = {-5; -1; 1; 5}
Mà n thuộc N
=> n thuộc {0; 4}.
Đúng 0
Bình luận (0)
a)2 vì 2+6 chia hết 2+2 =8 chia hết 4
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số nguyên n sao cho n2+9n+15 chia hết cho n+11
\(\Leftrightarrow n+11\in\left\{1;-1;37;-37\right\}\)
hay \(n\in\left\{-10;-12;26;-48\right\}\)
Đúng 1
Bình luận (0)
\(\Rightarrow n^2+11n-2n-22+37⋮n+11\\ \Rightarrow n\left(n+11\right)-2\left(n+11\right)+37⋮n+11\\ \Rightarrow n+11\inƯ\left(37\right)=\left\{-37;-1;1;37\right\}\\ \Rightarrow n\in\left\{-48;-12;-10;26\right\}\)
Đúng 0
Bình luận (0)
Bài toán 11. Tìm n biết rằng: n3 - n2 + 2n + 7 chia hết cho n2 + 1.
Bài toán 12. Tìm số tự nhiên n để 1n + 2n + 3n + 4n chia hết cho 5.
11:
n^3-n^2+2n+7 chia hết cho n^2+1
=>n^3+n-n^2-1+n+8 chia hết cho n^2+1
=>n+8 chia hết cho n^2+1
=>(n+8)(n-8) chia hết cho n^2+1
=>n^2-64 chia hết cho n^2+1
=>n^2+1-65 chia hết cho n^2+1
=>n^2+1 thuộc Ư(65)
=>n^2+1 thuộc {1;5;13;65}
=>n^2 thuộc {0;4;12;64}
mà n là số tự nhiên
nên n thuộc {0;2;8}
Thử lại, ta sẽ thấy n=8 không thỏa mãn
=>\(n\in\left\{0;2\right\}\)
Đúng 1
Bình luận (1)
b1: tìm số tự nhiên n sao cho
a) (n^10) +1 chia hết cho 10
b) (n^2) + 4n+29 chia hết cho 5
b2: tìm số nguyên n sao cho: (n^2)+2n-4 chia hết cho 11
Bài 4: Tìm số tự nhiên n sao cho:
a) 4n - 5 chia hết cho 2n - 1
b) n2 + 3n + 1 chia hết cho n +1
a,
Ta có: 4n-5 chia hết cho 2n-1
=>4n-2-3 chia hết cho 2n-1
=>2.(2n-1)-3 chia hết cho 2n-1
=>3 chia hết cho 2n-1
=>2n-1=Ư(3)=(-1,-3,1,3)
=>2n=(0,-2,2,4)
=>n=(0,-1,1,2)
Vậy n=0,-1,1,2
Đúng 0
Bình luận (0)
a,Tìm số nguyên n sao cho n-6 chia hết cho n-4
b, Tìm số nguyên n sao cho 2n-5 chia hết cho n-4
a/ theo đề bài ta có
n-4-2chia hết cho n-4
để n-6 chia hết cho n-4 thì 2 chia hết cho n-4
suy ra n-4 thuộc Ư2=[1;-1;2;-2] bạn tự tìm tiếp nhé
b;ui lười ứa ko làm tiếp
Đúng 0
Bình luận (0)
a) \(n-6⋮n-4\)
\(\Rightarrow n-4-2⋮n-4\)
\(\Rightarrow2⋮n-4\) ( vì \(n-4⋮n-4\) )
\(\Rightarrow n-4\in\text{Ư}_{\left(2\right)}=\text{ }\left\{1;-1;2;-2\right\}\)
lập bảng giá trị
| \(n-4\) | \(1\) | \(-1\) | \(2\) | \(-2\) |
| \(n\) | \(5\) | \(3\) | \(6\) | \(2\) |
vậy..................
b) \(2n-5⋮n-4\)
ta có \(n-4⋮n-4\)
\(\Rightarrow2\left(n-4\right)⋮n-4\)
\(\Rightarrow2n-8⋮n-4\)
mà \(2n-5⋮n-4\)
\(\Rightarrow2n-5-2n+8⋮n-4\)
\(\Rightarrow3⋮n-4\)
\(\Rightarrow n-4\in\text{Ư}_{\left(3\right)}=\text{ }\left\{1;-1;3;-3\right\}\)
lập bảng giá trị
| \(n-4\) | \(1\) | \(-1\) | \(3\) | \(-3\) |
| \(n\) | \(5\) | \(3\) | \(7\) | \(1\) |
vậy...............
Đúng 1
Bình luận (0)
a) Ta có n-6=n-4-2
=> 2 chia hết cho n-4
n nguyên => n-4 nguyên => n-4\(\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\)
ta có bảng
| n-4 | -2 | -1 | 1 | 2 |
| n | 2 | 3 | 5 | 6 |
vậy n={2;3;5;6} thỏa mãn yêu cầu đề bài
Xem thêm câu trả lời
Tìm n nguyên để n2 + 2n + 6 chia hết cho n + 4.
Bg
Ta có: n2 + 2n + 6 \(⋮\)n + 4 (n thuộc \(ℤ\))
=> 4n + 6 \(⋮\)n + 4
=> 4.(n + 4) - 10 \(⋮\)n + 4
Mà 4.(n + 4) \(⋮\)n + 4
=> 10 \(⋮\)n + 4
=> n + 4 thuộc Ư(10)
Ư(10) = {1; -1; 2; -2; 5; -5; 10; -10}
Lập bảng:
| n + 4 = | 1 | -1 | 2 | -2 | 5 | -5 | 10 | -10 |
| n = | -3 | -5 | -2 | -6 | 1 | -9 | 6 | -14 |
Vậy n = {-3; -5; ; -2; -6; 1; -9; 6; -14}
Ta có n2 + 2n + 6 = n2 + 8n + 16 - 6n - 24 + 14
= (n + 4)2 - (n + 4) + 14
= (n + 4)(n + 4 - 1) + 14
Vì (n + 4)(n + 4 - 1) \(⋮\)n + 4
=> 14 \(⋮n+4\Rightarrow n+4\inƯ\left(14\right)\)(Vì n nguyên)
=> \(n+4\in\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
=> \(n\in\left\{-3;-5;-2;-6;3;-11;10;-18\right\}\)
\(⋮\)