 giúp e câu 2,3,6,9 vs ạ em đang cần gấp T-T
giúp e câu 2,3,6,9 vs ạ em đang cần gấp T-T

Những câu hỏi liên quan
Giúp e vs ạ , e đang cần gấp ,em cảm ơn ạ

giúp em câu 2b vs, em đang cần gấp ạ
b: =(m-1)^2-4(-m^2-2)
=m^2+2m+1+4m^2+8
=5m^2+2m+9
=5(m^2+2/5m+9/5)
=5(m^2+2*m*1/5+1/25+44/25)
=5(m+1/5)^2+44/5>=44/5>0 với mọi m
=>PT luôn có hai nghiệm pb
Đúng 0
Bình luận (1)
Giúp em câu 16 vs ạ em đang cần gấp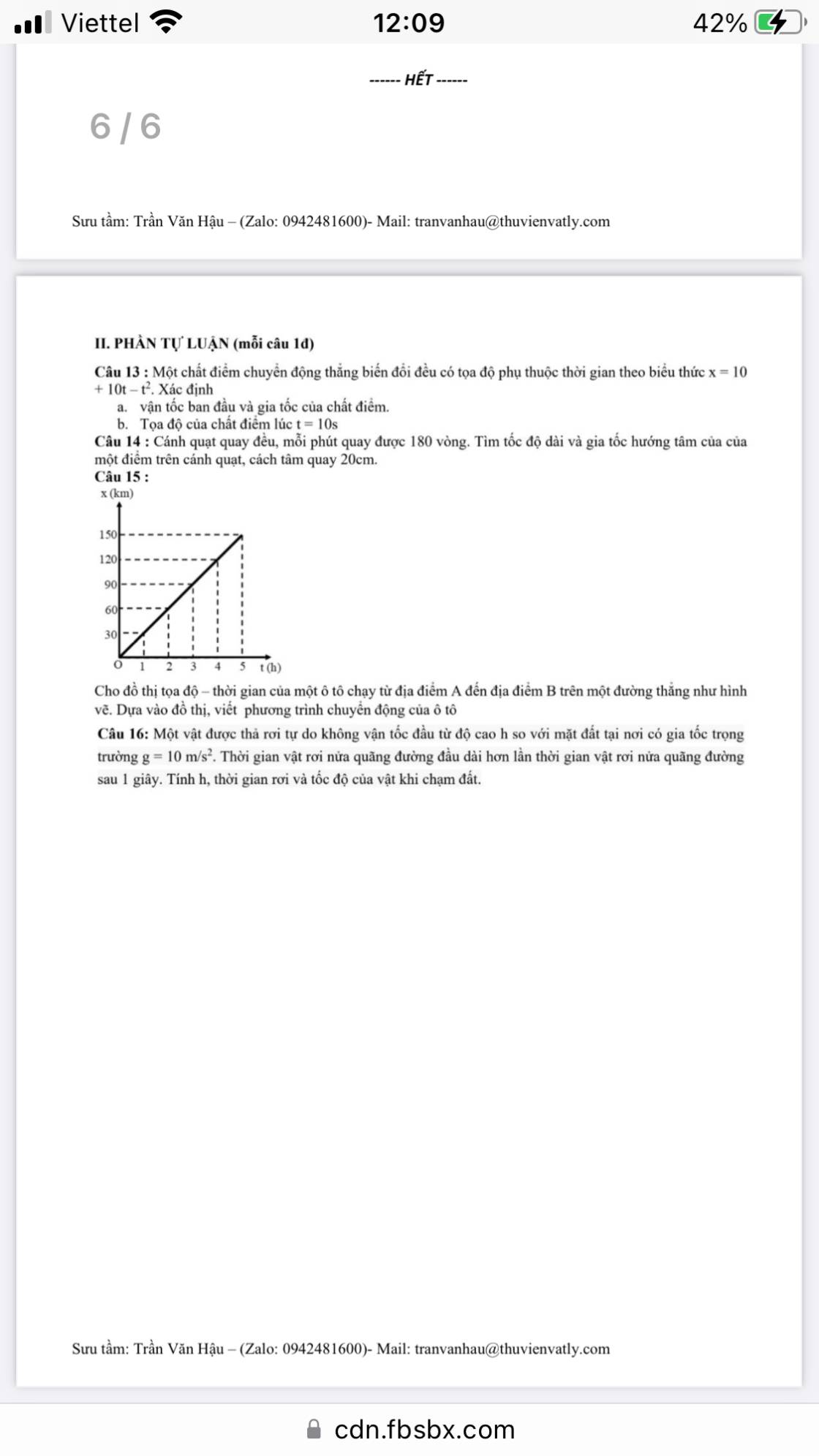
Giúp em câu này vs ạ em đang cần gấp
giải giúp em vs ạ e đang cần gấp.
Đọc tiếp
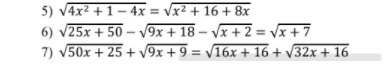
giải giúp em vs ạ e đang cần gấp.
cái thứ 2 em tải hình xuống đề phòng hình 1 mất ạ
Đúng 0
Bình luận (0)
giải giúp em vs ạ e đang cần gấp.
Đọc tiếp
giải giúp em vs ạ e đang cần gấp.
Bài 1:
1: \(\sqrt{3+2\sqrt{2}}=\sqrt{2}+1\)
2: \(\sqrt{5-2\sqrt{6}}=\sqrt{3}-\sqrt{2}\)
3: \(\sqrt{11-2\sqrt{30}}=\sqrt{6}-\sqrt{5}\)
4: \(\sqrt{7-2\sqrt{10}}=\sqrt{5}-\sqrt{2}\)
Đúng 0
Bình luận (0)
Giúp e vs ạ, em đang cần rất gấp, EM XIN CẢM ƠN ANH CHỊ Ạ!
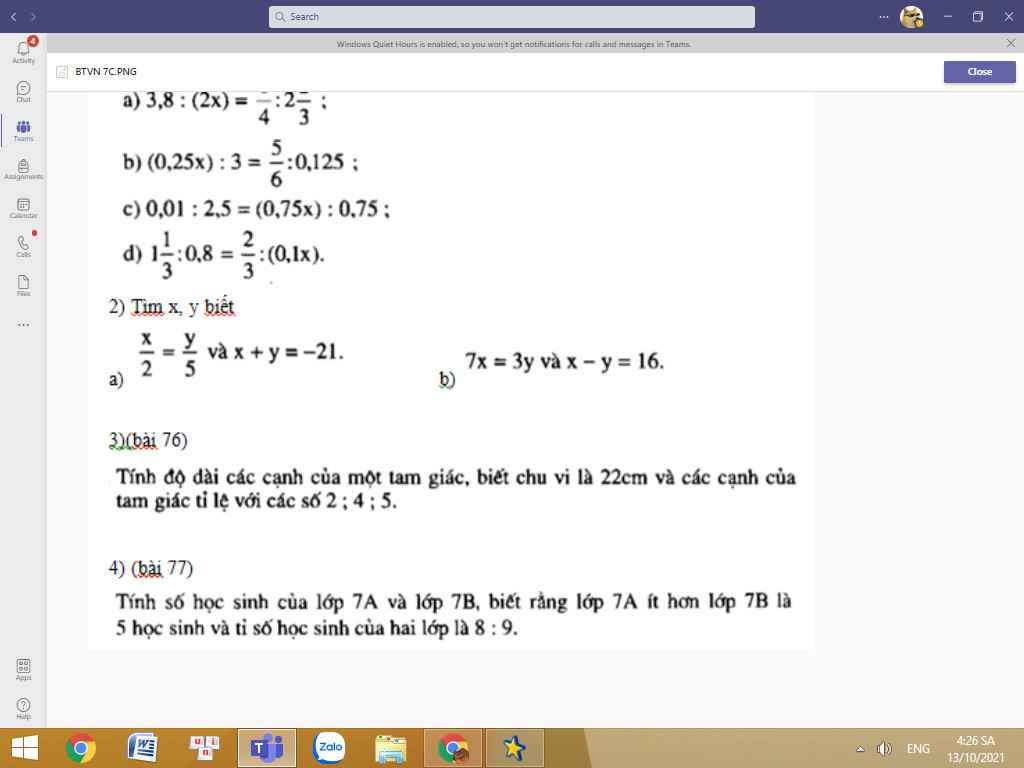 ai giúp em làm câu này vs em đang cần gấp ạ
ai giúp em làm câu này vs em đang cần gấp ạ
bài 2
x+y/2-5=-21/-3 =7
=> x=7.2 = 14
y=7.5 = 35
Đúng 0
Bình luận (0)
Bài 77:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{9}=\dfrac{y-x}{9-8}=5\)
Do đó: x=40; y=45
Đúng 0
Bình luận (0)
mn ơi giải giúp em vs ạ e đang cần gấp

1) \(\sqrt{2x-5}=7\)
\(\left(\sqrt{2x-5}\right)^2=7^2\)
\(2x-5=49\)
\(2x=54\)
\(x=27\)
2) \(3+\sqrt{x-2}=4\)
\(\sqrt{x-2}=1\)
\(\left(\sqrt{x-2}\right)^2=1^2\)
\(x-2=1\)
\(x=3\)
Đúng 0
Bình luận (0)
1) \(\sqrt{2x-5}=7\left(đk:x\ge\dfrac{5}{2}\right)\)
\(\Leftrightarrow2x-5=49\Leftrightarrow2x=54\Leftrightarrow x=27\left(tm\right)\)
2) \(3+\sqrt{x-2}=4\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{x-2}=1\Leftrightarrow x-2=1\Leftrightarrow x=3\)
3) \(\Leftrightarrow\sqrt{\left(x-1\right)^2}=1\Leftrightarrow\left|x-1\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
4) \(\Leftrightarrow\sqrt{\left(x-2\right)^2}=1\Leftrightarrow\left|x-2\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
5) \(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x+4\right)^2}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x+4\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+4\\2x-1=-x-4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
6) \(ĐK:x\ge-2\)
\(\Leftrightarrow5\sqrt{x+2}-3\sqrt{x+2}-\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow x+2=x+7\Leftrightarrow2=7\left(VLý\right)\)
Vậy \(S=\varnothing\)
7) \(ĐK:x\ge-1\)
\(\Leftrightarrow5\sqrt{2x+1}+3\sqrt{x+1}=4\sqrt{x+1}+4\sqrt{2x+1}\)
\(\Leftrightarrow\sqrt{2x+1}=\sqrt{x+1}\)
\(\Leftrightarrow2x+1=x+1\Leftrightarrow x=0\left(tm\right)\)
Đúng 1
Bình luận (1)
\(3,\sqrt{x^2-2x+1}=1\left(x\in R\right)\\ \Leftrightarrow\sqrt{\left(x-1\right)^2}=1\\ \Leftrightarrow\left|x-1\right|=1\Leftrightarrow\left[{}\begin{matrix}x-1=1\left(x\ge1\right)\\x-1=-1\left(x< 1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(tm\right)\end{matrix}\right.\)
\(4,ĐK:x\in R\\ PT\Leftrightarrow\sqrt{\left(x-2\right)^2}=1\\ \Leftrightarrow\left|x-2\right|=1\Leftrightarrow\left[{}\begin{matrix}x-2=1\left(x\ge2\right)\\x-2=-1\left(x< 2\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
\(5,ĐK:x\in R\\ PT\Leftrightarrow\left|2x-1\right|=\left|x+4\right|\\ \Leftrightarrow\left[{}\begin{matrix}2x-1=x+4\\1-2x=x+4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
\(6,ĐK:x\ge-2\\ PT\Leftrightarrow5\sqrt{x+2}-3\sqrt{x+2}-\sqrt{x+2}=\sqrt{x+7}\\ \Leftrightarrow\sqrt{x+2}=\sqrt{x+7}\Leftrightarrow x+2=x+7\Leftrightarrow0x=5\Leftrightarrow x\in\varnothing\)
\(7,ĐK:x\ge-1\\ PT\Leftrightarrow5\sqrt{x+2}+3\sqrt{x+1}=4\sqrt{x+1}+4\sqrt{x+2}\\ \Leftrightarrow\sqrt{x+2}=\sqrt{x+1}\\ \Leftrightarrow x+2=x+1\\ \Leftrightarrow0x=-1\Leftrightarrow x\in\varnothing\)
Đúng 3
Bình luận (1)