tìm số tự nhiên N để
25N^2 -97N+11 : N -4
2. Tìm n thuộc Z để
a, 2n^2 -n-7 chia hết cho n-2
b, 25n^2 - 97n +11 chia hết cho n-4
1.Tìm a,b biết x^3 + ax +b chia x+1 dư 7; chia cho x-3 dư -5
Câu 1.
Tìm a,b để \(x^3+ax+b\)chia \(x+1\)dư 7 và chia cho \(x-3\)dư -5.
Thương của phép chia đa thức bậc 3 \(x^3+ax+b\)cho \(x+1\)là 1 đa thức bậc 2 có hệ số bậc 2 bằng 1, tổng quát ở dạng: \(x^2+mx+n\).Số dư của phép chia này là 7 nên ta có:\(x^3+ax+b=\left(x+1\right)\left(x^2+mx+n\right)+7\mid\forall x\in R\)
\(\Leftrightarrow x^3+ax+b=x^3+\left(m+1\right)x^2+\left(m+n\right)x+n+7\mid\forall x\in R\)
Để 2 đa thức này bằng nhau với mọi x thuộc R thì hệ số các bậc phải bằng nhau. Đồng nhất chúng ta có:
\(\hept{\begin{cases}m+1=0\\m+n=a\\n+7=b\end{cases}\Rightarrow\hept{\begin{cases}m=-1\\n=a+1\\b=a+1+7\end{cases}\Rightarrow}b=a+8\mid\left(1\right)}\)
Tương tự với phép chia \(x^3+ax+b\)cho \(x-3\)dư -5.\(x^3+ax+b=\left(x-3\right)\left(x^2+px+q\right)-5\mid\forall x\in R\)
\(\Leftrightarrow x^3+ax+b=x^3+\left(p-3\right)x^2+\left(q-3p\right)x-\left(3q+5\right)\mid\forall x\in R\)
\(\Rightarrow\hept{\begin{cases}p-3=0\\q-3p=a\\-\left(3q+5\right)=b\end{cases}\Rightarrow\hept{\begin{cases}p=3\\q=a+9\\b=-\left(3\left(a+9\right)+5\right)\end{cases}\Rightarrow}b=-3a-32\mid\left(2\right)}\)
Từ (1) và (2) ta có:\(\hept{\begin{cases}b=a+8\\b=-3a-32\end{cases}\Rightarrow a+8=-3a-32\Rightarrow\hept{\begin{cases}a=-10\\b=-2\end{cases}}}\)
Vậy với \(a=-10;b=-2\)thì đa thức đã cho trở thành \(x^3-10x-2\)chia cho \(x+1\)dư 7 và chia cho \(x-3\)dư -5.Viết kết quả các phép chia này ta được:\(\hept{\begin{cases}x^3-10x-2=\left(x+1\right)\left(x^2-x-9\right)+7\\x^3-10x-2=\left(x-3\right)\left(x^2+3x-1\right)-5\end{cases}\mid\forall x\in R}\)
Tìm \(n\inℤđể\)
\(a,10n^2+n-10⋮n-1\)
\(b,25n^2-97n+11⋮n-4\)
\(a,10n^2+n-10⋮n-1\)
\(10n^2-10n+11n-11+1⋮n-1\)
Do \(10n\left(n-1\right)⋮n-1;11\left(n-1\right)⋮n-1\Rightarrow1⋮n-1\)
\(\Rightarrow n-1\in\left(1;-1\right)\)
\(\Rightarrow n\in\left(2;0\right)\)
\(b,25n^2-97n+11⋮n-4\)
\(25n^2-100n+3n-12+23⋮n-4\)
\(25n\left(n-4\right)+3\left(n-4\right)+23⋮n-4\)
\(\Rightarrow23⋮n-4\)
\(\Rightarrow n-4\in\left(1;-1;23;-23\right)\)
\(\Rightarrow n\in\left(5;3;27;-19\right)\)
tìm n thuộc Z sao cho
a 10n2 +n - 10 chia hết cho n-1
b 25n2 -97n +11 chi hết cho n-4
Gọi thương của phép chia này là A (A nguyên), thì ta có
\(\frac{10n^2+n-10}{n-1}=10n+11+\frac{1}{n-1}\)
Để A nguyên thì n - 1 phải là ước của 1 hay (n - 1) = (1, -1)
=> n = (2, 0)
Câu còn lại tương tự
Cho tâm giac ABC vương tại A đường trung tuyến Âm . Gọi I là trung điểm AC ,K là điểm đối xứng vs H qua AC chứng minh:
a)D đối xứng E qua A
B) tâm GIAC DHE vuông
c)tu giác BDEC là hình thang vuông
D)BC=BD+CE
Ah. Mình thật sự xin lỗi mình nhập lộn nhé. Thôi có gì thì mọi người ai pít giải hộ mình luon nha
Tìm số tự nhiên n thỏa mãn 25n = 5.125?
A. n = 2 B. n = 4 C. n = 5 D. n = 25
Câu 28: Tìm số tự nhiên n thỏa mãn 25n = 52.54?
A. n = 3 B. n = 4 C. n = 8 D. n = 16
Tìm số tự nhiên n thỏa mãn 25 n = 5 2 . 5 4 ?
A. n = 3
B. n = 16
C. n = 8
D. n = 4
Đáp án: A
25
n
=
5
2
.
5
4
5
2
n
=
5
6
2n=6
n=3
Tìm số tự nhiên n thỏa mãn 25 n : 25 3 = 25 5 ?
A. n = 3
B. n = 6
C. n = 7
D. n = 8
Đáp án là D
Ta có: 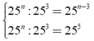 nên n - 3 = 5 suy ra n = 8
nên n - 3 = 5 suy ra n = 8
Tìm số tự nhiên n sao cho :
a/ 25n+3 chia hết cho 53
b/ 4n-5chia hết cho 13
c/ 5n+1chia hết cho 7
d/ 3n-4 chia hết cho 11
Tìm số tự nhiên n sao cho:
a/ 25n+3 chia hết cho 53
b/ 4n-5 chia hết cho 13
c/ 5n+1 chia hết cho 7
d/ 3n-4 chia hết cho 11