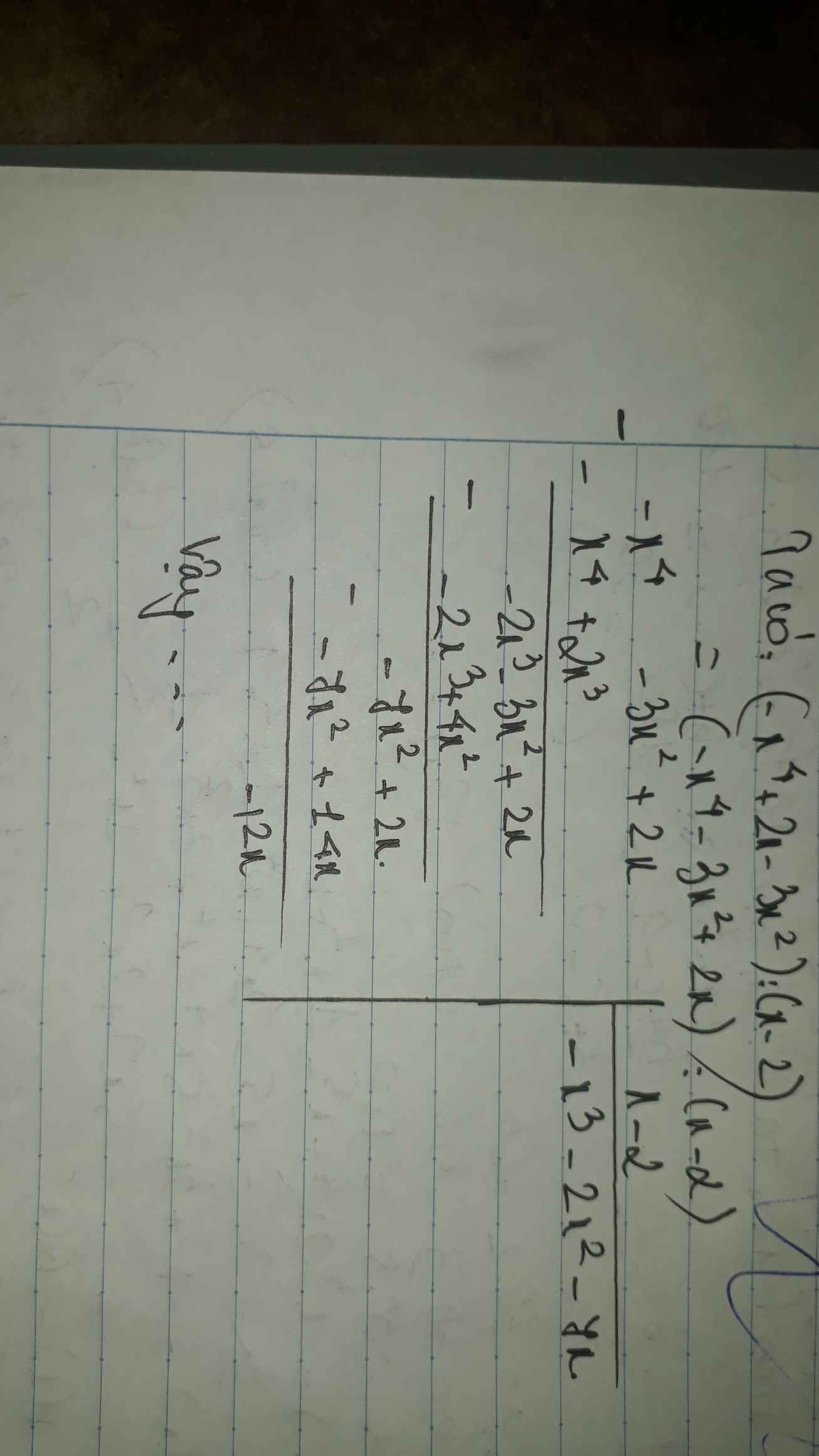Thực hiện phép chia: (đơn thức-đa thức)
(-x^4+2x-3x^2)

Những câu hỏi liên quan
Thực hiện phép chia: (đơn thức-đa thức)
(-x^4+2x-3x^2) : (x-2)
`(-x^4+2x-3x^2):(x-2)`
`=[-x(x^3+3x-2)]:(x-2)`
`=[-x(x^3-2x^2+2x^2-4x+7x-14+12)]:(x-2)`
`={-x[x^2(x-2)+2x(x-2)+7(x-2)]-12x+24-24}:(x-2)`
`=[-x(x-2)(x^2+2x+7)-12(x-2)-24]:(x-2)`
`=-x(x^2+2x+7)-12` và dư `-24`
`=-x^3-2x^2-7x-12` và dư `-24`
Đúng 2
Bình luận (0)
\(\dfrac{-x^4-3x^2+2x}{x-2}\)
\(=\dfrac{-x^4+2x^3-2x^3+4x^2-7x^2+14x-12x+24-24}{x-2}\)
\(=-x^3-2x^2-7x-12-\dfrac{24}{x-2}\)
Đúng 0
Bình luận (0)
Thực hiện phép chia: (đơn thức-đa thức)
(-x4+2x-3x2):(x-2)
\(\dfrac{-x^4-3x^2+2x}{x-2}\)
\(=\dfrac{-x^4+2x^3-2x^3+4x^2-7x^2+14x-12x+24-24}{x-2}\)
\(=-x^3-2x^2-7x-12+\dfrac{-24}{x-2}\)
Đúng 0
Bình luận (0)
Cho đa thức A(x)=x^4+2x^2-3x+a và B(x)=2x-1
a. Tìm đa thức dư khi thực hiện phép chia A(x) cho B(x)
b. Tìm a để A(x) chia hết cho B(x)
b: \(\dfrac{A\left(x\right)}{B\left(x\right)}=\dfrac{x^4-\dfrac{1}{2}x^3+\dfrac{1}{2}x^3-\dfrac{1}{4}x^2+\dfrac{9}{4}x^2-\dfrac{9}{8}x-\dfrac{15}{8}x+\dfrac{15}{16}+a-\dfrac{1}{16}}{2x-1}\)
Để A(x) chia hết cho B(x) thì a-1/16=0
hay a=1/16
Đúng 0
Bình luận (0)
ôn tập chương 1
I; nhân đơn thức với đa thức-nhân đa thức với đa thức
bt1;thực hiện phép tính
a) (x^2-1)(x^2+2x) c) (x+3)x^2+3x-5)
d) (x+1)(x^2-x+1) e) (2x^2-3x-1))5x+2)
f) (x^2-3x+3)(x-4)
Bài 1: Thực hiện phép tính(Phép chia đa thức cho đa thức có dư)
(2x^2-3x^2-3)÷(x^2-1).
Thực hiện phép chia đa thức
a) (x\(^3\) + x\(^2\) – 2x ): (x + 2)
b) (2x-3x\(^2\) + x\(^3\) + 24) : ( x+2 )
a: \(=\dfrac{x\left(x^2+x-2\right)}{x+2}=\dfrac{x\left(x+2\right)\left(x-1\right)}{x+2}=x^2-x\)
b: \(=\dfrac{x^3-3x^2+2x+24}{x+2}=\dfrac{x^3+2x^2-5x^2-10x+12x+24}{x+2}=x^2-5x+12\)
Đúng 0
Bình luận (0)
Thực hiện phép chia: (chia đa thức - đơn thức)
\(-\dfrac{1}{3}\)x5y2 : (-2xy)-(x2+2x+1) : (x+1)
`-1/3x^5y^2:(-2xy)-(x^2+2x+1):(x+1)`
`=-1/3:(-2).(x^5:x).(y^2:y)-(x+1)^2:(x+1)`
`=-1/6x^4y-(x+1)`
`=-1/6x^4y-x-1`
Đúng 0
Bình luận (0)
\(\dfrac{-1}{3}x^5y^2:\left(-2xy\right)-\left(x^2+2x+1\right):\left(x+1\right)\)
\(=\dfrac{1}{6}x^4y-x-1\)
Đúng 0
Bình luận (0)
Bài 1 (1,0 điểm).a) Phân tích đa thức sau thành nhân tử: x²(y – 1) – 4(y – 1)b) Tính nhanh giá trị biểu thức: x² + 2x +1- y? tại x 84 và y 15Bài 2 (1,5 điểm). Cho đa thức A x³ + 3x? + 3x - 2 và đa thức B x+1a) Thực hiện phép chia đa thức A cho đa thức B.b) Tìm các giá trị nguyên của x để giá trị đa thức A chia hết cho giá trị của đa thức B. Mọi người giúp em với ạ
Đọc tiếp
Bài 1 (1,0 điểm).
a) Phân tích đa thức sau thành nhân tử: x²(y – 1) – 4(y – 1)
b) Tính nhanh giá trị biểu thức: x² + 2x +1- y? tại x = 84 và y = 15
Bài 2 (1,5 điểm). Cho đa thức A =x³ + 3x? + 3x - 2 và đa thức B =x+1
a) Thực hiện phép chia đa thức A cho đa thức B.
b) Tìm các giá trị nguyên của x để giá trị đa thức A chia hết cho giá trị của đa thức B.
Mọi người giúp em với ạ
\(x^2\left(y-1\right)-4\left(y-1\right)\\ =\left(y-1\right)\left(x^2-4\right)=\left(y-1\right)\left(x-2\right)\left(x+2\right)\)
Đúng 2
Bình luận (2)
\(=\left(y-1\right)\left(x-2\right)\left(x+2\right)\)
Đúng 2
Bình luận (0)
\(x^2\left(y-1\right)-4\left(y-1\right)\\ =\left(x^2-4\right)\left(y-1\right)\\ =\left(x-2\right)\left(x+2\right)\left(y-1\right)\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Dạng 3: Chia đa thức cho đơn thức
bài 3: thực hiện phép chia
a/ (4x^3 y^2 - 8x^2y +10xy):(2xy) b/ (7x^4 y^2 -2x^2y^2 -5x^3y^4):(3x^2y)
DÚP MÌNH VỚI NHA NHANH LÊN Ạ
a: \(=\dfrac{2xy\left(2x^2y-4x+5\right)}{2xy}=2x^2y-4x+5\)
b: \(=\dfrac{x^2y\left(7x^2y-2y-5x^2y^3\right)}{3x^2y}=\dfrac{7}{3}x^2y-\dfrac{2}{3}y-\dfrac{5}{3}x^2y^3\)
Đúng 1
Bình luận (0)