Chứng minh:1/AD^2=1/AM^2+1/AM^2

Những câu hỏi liên quan
cho tam giác ABC có trung tuyến AM ,điểm I thuộc đoạn thẳng AM ,BI cắt AC ở I
a) nếu AD = 1/2 DC chứng minh I là trung điểm AM
b) nếu I là trung điểm AM chứng minh AD = 1/2 DC , ID=1/4 BD
c) nếu AD = 1/2 DC khi đó trên cạnh AD lấy điểm E sao cho AB =3AE chứng minh BD, CE,AM đồng quy
a: Gọi K là trung điểm của DC
Suy ra: AD=DK=KC
Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của CD
Do đó: MK là đường trung bình của ΔBDC
Suy ra: MK//ID
Xét ΔAMK có
D là trung điểm của AK
DI//MK
Do đó: I là trung điểm của AM
Đúng 1
Bình luận (0)
cho tam giác abc có trung tuyến am , i là một điểm thuộc đoạn thẳng am bi cắt ac ở d a, nếu ad=1/2dc khi đó hãy chứng minh i là trung điểm của am b, nếu i là trung điểm của am khi đó cm ad = 1/2 dc id = 1/4 bd c, nếu ad = 1/2 dc lhi đó trên cạnh ab ấy điểm e sao cho ab =3ae chứng minh bd, ce, am đồng quy
Hình vuông ABCD, E thuộc BC. Tia AE cắt đường thẳng CD tại N, vẽ đoạn AM vuông góc AE và AM=AE, (E và M thuộc 2 nửa mặt phẳng đối nhau bờ AD).
a) Chứng minh: C, D, M thẳng hàng.
b) Chứng minh: 1/AD² =1/AE² + 1/AN²
c) Cho AB=10cm, DM/DN=1/4. Tính tỉ số AM/AN và tích AM×AN
Bài 1:Cho tam giác ABC vuông tại A có AM là đường trung tuyến.Gọi N là trung điểm của AC
1)Chứng minh MNperp AC
2)Tam giác AMC là tam giác gì?Vì sao?
3)Chứng minh 2AMBC
Bài 2:Cho tam giác ABC nhọn có 2 đường cao BD và CE.Gọi M,N là trung điểm của BC và DE
1)Chứng minh DMdfrac{1}{2}BC
2)Chứng minh tam giác DME cân
3)Chứng minh MN perp DE
Bài 3:Cho tam giác ABC trên AC lấy theo thứ tự điểm D và E sao cho ADDEEC.Gọi M là trung điểm của BC,BD cắt AM tại I
1)Chứng minh ME//BD
2)Chứng minh I...
Đọc tiếp
Bài 1:Cho tam giác ABC vuông tại A có AM là đường trung tuyến.Gọi N là trung điểm của AC
1)Chứng minh \(MN\perp AC\)
2)Tam giác AMC là tam giác gì?Vì sao?
3)Chứng minh 2AM=BC
Bài 2:Cho tam giác ABC nhọn có 2 đường cao BD và CE.Gọi M,N là trung điểm của BC và DE
1)Chứng minh \(DM=\dfrac{1}{2}BC\)
2)Chứng minh tam giác DME cân
3)Chứng minh MN \(\perp\) DE
Bài 3:Cho tam giác ABC trên AC lấy theo thứ tự điểm D và E sao cho AD=DE=EC.Gọi M là trung điểm của BC,BD cắt AM tại I
1)Chứng minh ME//BD
2)Chứng minh I là trung điểm của AM
3)Chứng minh ID=\(\dfrac{1}{4}\) BD
Bài 4:Cho tam giác ABC có AM là trung tuyến.Lấy D thuộc AC sao cho \(AD=\dfrac{1}{2}DC\).Kẻ ME//BD (E thuộc CD), BD cắt AM tại I
1)Chứng minh AD=DE=EC
2)Chứng minh I là trung điểm AM
a)Ta có: BM=MC; AN=NC
=>MN là đường trung bình của ΔABC
=>MN//AB
Mà ∠BAC đồng vị với ∠MNC nên ∠BAC=∠MNC=90*
Hay MN ⊥AC
b) Ta có : MN⊥AC(câu a)
=> Mn là đường cao của ΔAMC
Mà AN=MC=> đường cao cũng là đường trung tuyến
Hay ΔAMC cân tại M
c) Ta có: AM là đường trung tuyến của ΔABC
=>BM=MC.
Ta lại có MC=BM=1/2BC=>BC=2MC
Mà MC=AM(do ΔAMC cân tại A)=>BC=2AM
Đúng 0
Bình luận (0)
cho hình vuông ABCD , ,AM\(\cap\) BC ở E , d⊥AM ở A , d ⊥CD ở N , O là trung điểm EN. chứng minh :
a) B,D,O thẳng hàng
b) \(\frac{1}{AB^2}=\frac{1}{AM^2}+\frac{1}{AE^2}\)
c)OA⊥NE
d)\(\frac{1}{AD^2}\)≥\(\frac{2}{AM.AE}\)
Cho tam giác ABC có trung tuyến AM, I là một điểm thuộc đoạn thẳng AM, BI cắt AC ở Đâu.
a) Nếu AD = 1/2 DC. Khi đó hãy chứng minh I là trung điểm của AM.
b) Nếu I là trung điểm của AM. Khi đó hãy chứng minh AD = 1/2 DC và ID = 1/4 BD
c) Nếu AD = 1/2 DC. Khi đó trên cạnh AB lấy điểm E sao cho AB= 3AE. Chứng minh BD, CE, AM đồng qui
Các bạn giúp mìk vs đag cần gấp
â)Gọi H là trung điểm CD
=> CH=HD=AD (gt)
Xét tam giác BDC , co :
CH =HD (cmt)
BM=MC (gt)
=> MH là đường trung bình
=> MH //BD
Xét tam giácAMH , co :
MH // BD (cmt)
AD = DH (cmt)
=> AI = IM
=> I la trung diem AM
b) Gọi H là trung điểm CD
=>CH=HD
Xet tam giac BCD , co :
CH =HD (cmt)
BM=MC (gt)
=> MH la duong trung binh
=> MH //BD va MH=\(\dfrac{BD}{2}\)
Xét tam giác AMH , cờ :MH // BD (cmt )
AI =IM (gt) (1)
=> AD =HD ( => AD=\(\dfrac{1}{2}\)DC ) (2)
Tu (1) va (2) => ID la duong trung binh
=> ID =\(\dfrac{MH}{2}\) =\(\dfrac{BD}{2}\) : 2=\(\dfrac{BD}{4}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A ; M là trung điểm của BC . trên tia AM lấy D sao cho AD = 2AM
a, chứng minh AB = CD
b, chứng minh BD // AC
c, chứng minh AM = \(\dfrac{1}{2}\) BC
d, chứng minh tam giác MCD là tam giác vuông cân
a) Theo giả thiết ta có : \(AD=2AM\)
=> AM = DM
Xét \(\Delta ABM;\Delta DCM\) có :
\(BM=MC\left(gt\right)\)
\(\widehat{BMA}=\widehat{DMC}\) (đối đỉnh)
=> \(\Delta ABM=\Delta DCM\left(c.g.c\right)\)
=> \(AB=CD\) ( 2 cạnh tương ứng)
b) Xét \(\Delta BMD;\Delta AMC\) có :
\(BM=MC\left(gt\right)\)
\(\widehat{BMD}=\widehat{AMC}\) (đối đỉnh)
\(AM=MD\left(cmt\right)\)
=> \(\Delta BMD=\Delta AMC\left(c.g.c\right)\)
=> \(\widehat{BDM}=\widehat{CAM}\) (2 góc tương ứng)
Mà thấy : 2 góc này ở vị trí so le trong
=> \(\text{BD // AC (đpcm)}\)
c) Xét \(\Delta ABC;\Delta ACD\) có :
\(AB=CD\) (cmt - câu a)
\(\widehat{ABC}=\widehat{ADC}\) (do \(\Delta ABM;\Delta DCM\) )
\(BD=AC\) (do \(\Delta BMD=\Delta AMC\left(c.g.c\right)\)
=> \(\Delta ABC=\Delta ACD\left(c.g.c\right)\)
=> \(AD=BC\) (2 cạnh tương ứng)
Mà có : \(AM=\dfrac{1}{2}AD\) (gt)
Cho nên : \(AM=\dfrac{1}{2}BC\left(đpcm\right)\)
Đúng 0
Bình luận (1)
1, Chứng minh đẳng thức frac{1}{left(a-bright)^2}+frac{1}{left(b-cright)^2}+frac{1}{left(c-aright)^2}left(frac{1}{a-b}+frac{1}{b-c}+frac{1}{c-a}right)^22, Cho tam giác ABC có AM và AD lần lượt là các đường trung tuyến và phân giác. Đường thẳng qua M và song song với AB cắt AD tại E. Đường thẳng qua D và song song với AC cắt AM tại F. Chứng minha. Góc AEC 90 độb. E, F, C thẳng hàng
Đọc tiếp
1, Chứng minh đẳng thức \(\frac{1}{\left(a-b\right)^2}+\frac{1}{\left(b-c\right)^2}+\frac{1}{\left(c-a\right)^2}=\left(\frac{1}{a-b}+\frac{1}{b-c}+\frac{1}{c-a}\right)^2\)
2, Cho tam giác ABC có AM và AD lần lượt là các đường trung tuyến và phân giác. Đường thẳng qua M và song song với AB cắt AD tại E. Đường thẳng qua D và song song với AC cắt AM tại F. Chứng minh
a. Góc AEC = 90 độ
b. E, F, C thẳng hàng
cho tam giác ABC vuông cân tại A có : M là trung diểm của BC . trên tia AM lấy D sao cho AD= 2 . AM. chứng minh :
a, AB =CD
b, BD // AC
c, AM = \(\dfrac{1}{2}\) BC
d, tam giác MCD là tam giác vuông cân
a) Xét \(\Delta ABM;\Delta DCM\) có :
\(BM=MC\left(gt\right)\)
\(\widehat{BMA}=\widehat{DMC}\left(đ^2\right)\)
\(AM=MC\left(AD=2AM-gt\right)\)
=> \(\Delta ABM;\Delta DCM\)(c.g.c)
=> \(AB=CD\) ( 2 cạnh tương ứng)
b) Ta dễ dàng chứng minh được : \(\Delta BMD=\Delta AMC\left(c.g.c\right)\)
=> \(\widehat{BDM}=\widehat{CAM}\) (2 góc tương ứng)
Mà thấy : 2 góc này ở vị trí so le trong
=> BD // AC (đpcm)
c) Ta dễ dàng chứng minh được \(\Delta ABC=\Delta CAD\left(c.g.c\right)\)
Từ đó có : \(AD=BC\) ( 2 cạnh tương ứng)
Mà có : \(AD=2AM\Rightarrow AM=\dfrac{1}{2}AD\)
Hay : \(AM=\dfrac{1}{2}BC\) (đpcm)
d) Ta có : \(\left\{{}\begin{matrix}AM=\dfrac{1}{2}AD\Rightarrow AM=MD\\AM=\dfrac{1}{2}BC\Rightarrow AM=MC\end{matrix}\right.\)
Suy ra : \(MC=MD\left(=AM\right)\)
Xét \(\Delta MCD\) có :
MC = MD (cmt)
=> \(\Delta MCD\) cân tại M
Đúng 0
Bình luận (1)
a/ Vì \(AD=2AM\Rightarrow AM=DM=\dfrac{AD}{2}\)
Xét \(\Delta BAM\) và \(\Delta CDM\) có:
\(AM=DM\left(cmt\right)\)
\(\widehat{M_1}=\widehat{M_2}\) ( đối đỉnh )
\(BM=CM\) ( M là trung điểm của BC )
Do đó \(\Delta BAM=\Delta CDM\left(c.g.c\right)\)
\(\Rightarrow AB=CD\) ( cạnh tương ứng )
b/ Xét \(\Delta BMD\) và \(\Delta CMA\) có:
\(BM=CM\) ( M là trung điểm BC )
\(\widehat{M_3}=\widehat{M_4}\) ( đối đỉnh )
\(AM=DM\left(cmt\right)\)
Do đó \(\Delta BMD=\Delta CMA\left(c.g.c\right)\Rightarrow\widehat{B_1}=\widehat{C_1}\) ( góc tương ứng )
Xét hai vị trí này thuộc 2 vị trí so le trong, suy ra \(BD\text{//}AC\)
Đúng 0
Bình luận (0)
AD=2.AM nên AM+MD=AD nên AM=MD
a) Xét \(\Delta\)AMB và MDC có
MB=MC(M là trung điểm BC)
\(\widehat{M}1=\widehat{M}2\)(đối đỉnh)
MA=MD
\(\Rightarrow\)\(\Delta\)AMB=\(\Delta\)MDC(c.g.c)
nên AB=CD và \(\widehat{B2}=\widehat{C2}\Rightarrow AB//CD\)
b) Xét \(\Delta\)BMD và \(\Delta\)CMA có
MA=MD
\(\widehat{M}3=\widehat{M}4\)(đối đỉnh)
MB=MC(M là trung điểm BC)
\(\Rightarrow\)\(\Delta\)BMD=\(\Delta\)CMA(c.g.c)
nên \(\widehat{B}1=\widehat{C1}\)
MÀ 2 góc này ở vị trí so le trong
\(\Rightarrow BD//AC\)
c) \(\Delta\)ABC vuông cân tại A nên \(\widehat{ABC}=\widehat{ACB}=45^0\)
MÀ \(\widehat{B}1=\widehat{C1}\)và \(\widehat{B2}=\widehat{C2}\)nên
\(\widehat{C1}+\widehat{C2}=\widehat{ACD}=\widehat{BAC}=90^0\)
Xét \(\Delta\)ACB và \(\Delta\)ACD có
Ac chung
\(\widehat{ACD}=\widehat{BAC}\)(cmt)
AB=CD
\(\Rightarrow\)\(\Delta\)ACB=\(\Delta\)ACD(c.g.c)
nên BC=AD
Mà AM=\(\dfrac{1}{2}\)AD
nên AM=\(\dfrac{1}{2}\)BC
d) MB=MC=AM=\(\dfrac{1}{2}\)BC
mà AM=MD
nên MD=MC
\(\Rightarrow\Delta MCD\) cân tại M (1)
TRong \(\Delta\)ABC có AM là đường trung tuyến nên Am là phân giác \(\widehat{BAC}\Rightarrow\widehat{A1}=\widehat{A2}=45^0\);\(\widehat{B2}=\widehat{C2}\)
nên \(\widehat{D1}+\widehat{C2}=90^0\Rightarrow\widehat{M2}=90^0\)(2)
(1)(2) \(\Rightarrow\Delta MCD\)vuông cân tại M
Mà \(\widehat{A}1\)=\(\widehat{D1}\);
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
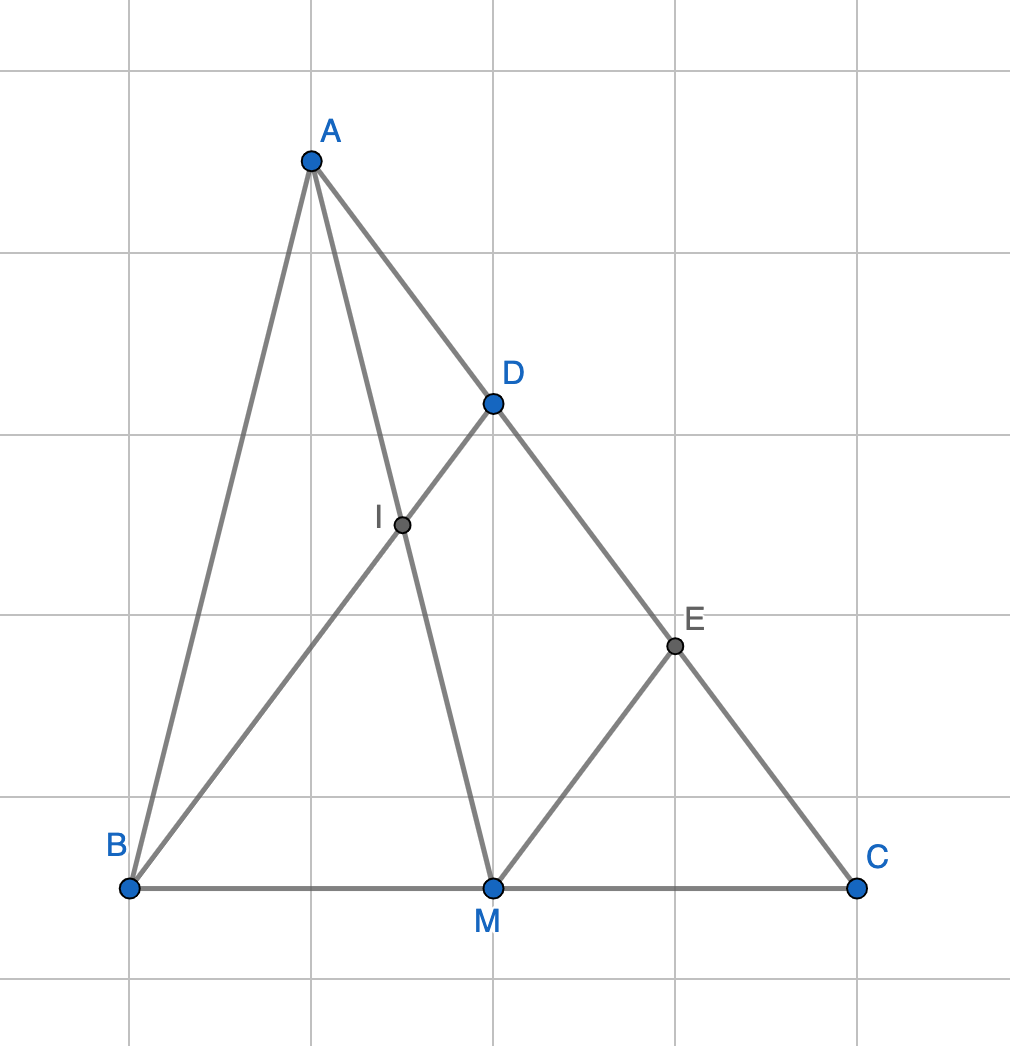
Cho tam giác ABC, trung tuyến AM . Lấy D trên AC sao cho DA= \(\dfrac{1}{2}\)DC .Gọi I là giao điểm của AM và DB , gọi E là trung điểm DC
a, chứng minh AD=DE=EC
b, Chứng minh DEMB là hình thang
C, Chứng minh IA=IM
a) Ta có: \(AD=\dfrac{1}{2}DC\)(gt)
mà \(EC=ED=\dfrac{DC}{2}\)(E là trung điểm của DC)
nên AD=EC=ED
b) Xét ΔCDB có
M là trung điểm của BC(gt)
E là trung điểm của CD(gt)
Do đó: ME là đường trung bình của ΔCDB(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//BD và \(ME=\dfrac{1}{2}BD\)(Định lí 2 về đường trung bình của tam giác)
hay ME//ID
Xét tứ giác MEDB có ME//BD(cmt)
nên MEDB là hình thang có hai đáy là ME và BD(Định nghĩa hình thang)
c) Xét ΔAME có
D là trung điểm của AE(AD=DE, D nằm giữa A và E)
DI//ME(cmt)
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
hay IA=IM(Đpcm)
Đúng 2
Bình luận (0)
\(a.\) Ta có: DA=\(^{\dfrac{1}{2}DC=DE=EC}\) (đpcm)
\(b.\) Xét tam giác DBC có:
\(\left\{{}\begin{matrix}DE=CE\\BM=CM\end{matrix}\right.\) \(\Rightarrow\) ME là đường trung bình tam giacs DBC
\(\Rightarrow ME\)//\(BD\) \(\Rightarrow\) DEMB là hình thang
\(c.\)Vì \(\Rightarrow ME\)//\(BD\) nên ME // ID
Xét tam giác AMD có: \(\left\{{}\begin{matrix}ME\backslash\backslash ID\\AD=DC\end{matrix}\right.\)
=> ME là đường trung bình tam giác AMD hay I là trung điểm MA
\(\Rightarrow IA=IM\) (đpcm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời






















