Tìm a,b,c biết:\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)và a2-b2+2c2=108

Những câu hỏi liên quan
Tìm 2 số a, b biết :
a) \(\dfrac{a}{5}\) = \(\dfrac{b}{4}\) và a2 – b2 = 1
b) \(\dfrac{a}{2}\) = \(\dfrac{b}{3}\) = \(\dfrac{c}{4}\) và a2 - b2 + 2c2 = 108
a) \(\dfrac{a}{5}=\dfrac{b}{4}\Rightarrow\dfrac{a^2}{25}=\dfrac{b^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{25}=\dfrac{b^2}{16}=\dfrac{a^2-b^2}{25-16}=\dfrac{1}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{1}{9}\cdot25=\dfrac{25}{9}\\b^2=\dfrac{1}{9}\cdot16=\dfrac{16}{9}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3};b=\dfrac{4}{3}\\a=\dfrac{-5}{3};b=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(\left(a;b\right)\in\left\{\left(\dfrac{5}{3};\dfrac{4}{3}\right);\left(-\dfrac{5}{3};-\dfrac{4}{3}\right)\right\}\)
b) \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=4.4=16\\b^2=4.9=36\\c^2=4,16=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=4;=6;c=8\\a=-4;b=-6;c=-8\end{matrix}\right.\)
Vậy (a;b;c) \(\in\left\{\left(4;6;8\right);\left(-4;-6;-8\right)\right\}\)
Đúng 2
Bình luận (0)
Tìm a,b,c biết: \(\dfrac{a}{2}\), \(\dfrac{b}{3}\), \(\dfrac{c}{4}\) biết a2-b2+2c2=108
Sửa \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\Rightarrow a=2k;b=3k;c=4k\)
\(a^2-b^2+2c^2=108\\ \Rightarrow4k^2-9k^2+32k^2=108\\ \Rightarrow27k^2=108\Rightarrow k^2=4\\ \Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4;y=6;z=8\\x=-4;y=-6;z=-8\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a^2}{2^2}=\dfrac{b^2}{3^2}=\dfrac{2c^2}{2.4^2}=\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}\)
Áp dụng tcdtsbn , ta có:
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a=8\\b=12\\c=16\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Tìm các số a,b,c biết rằng: a 2 = b 3 = c 4 và a2 – b2 + 2c2 = 108
Ta có:
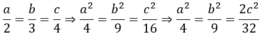
Theo tính chất dãy tỉ số bằng nhau ta có:
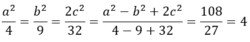
Ta có:
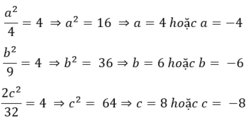
Mà 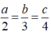 nên a, b và c cùng dấu.
nên a, b và c cùng dấu.
Vậy ta tìm được các số a1 = 4; b1 = 6; c1 = 8 hoặc a2 = -4; b2 = -6 và c2 = -8
Đúng 0
Bình luận (0)
Tìm a, b, c, biết:
a
2
=
b
3
=
c
4
và a
2 − b
2 + 2c
2 = 108
Đặt \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k\)
=>a=2k; b=3k; c=4k
\(a^2-b^2+2c^2=108\)
=>\(\left(2k\right)^2-\left(3k\right)^2+2\cdot\left(4k\right)^2=108\)
=>\(4k^2-9k^2+2\cdot16k^2=108\)
=>\(27k^2=108\)
=>\(k^2=4\)
=>\(\left[\begin{array}{l}k=2\\ k=-2\end{array}\right.\)
TH1: k=2
=>\(\begin{cases}a=2\cdot2=4\\ b=3\cdot2=6\\ c=4\cdot2=8\end{cases}\)
TH2: k=-2
=>\(\begin{cases}a=2\cdot\left(-2\right)=-4\\ b=3\cdot\left(-2\right)=-6\\ c=4\cdot\left(-2\right)=-8\end{cases}\)
Đúng 0
Bình luận (0)
Tìm ba số a, b, c biết:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\) và \(a^2-b^2+2c^2=108\)
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\Rightarrow\frac{a^2}{2^2}=\frac{b^2}{3^2}=\frac{2c^2}{2.4^2}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a^2}{2^2}=\frac{b^2}{3^2}=\frac{2c^2}{2.4^2}=\frac{a^2-b^2+2c^2}{4-9+2.4^2}=\frac{108}{27}=4=2^2\)
\(\Rightarrow\begin{cases}a^2=2^2.2^2=4^2\\b^2=2^2.3^2=6^2\\c^2=2^2.2.4^2:2=8^2\end{cases}\)\(\Rightarrow\begin{cases}a\in\left\{4;-4\right\}\\b\in\left\{6;-6\right\}\\c\in\left\{8;-8\right\}\end{cases}\)
Vậy giá trị (a;b;c) thỏa mãn đề bài là: (4;6;8) ; (-4;-6;-8)
Đúng 0
Bình luận (0)
Giải:
Đặt \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k\)
\(\Rightarrow a=2k,b=3k,c=4k\)
Ta có: \(a^2-b^2+2c^2=108\)
\(\Rightarrow\left(2k\right)^2-\left(3k\right)^2+2\left(4k\right)^2=108\)
\(\Rightarrow2^2.k^2-3^2.k^2+2.4^2.k^2=108\)
\(\Rightarrow4.k^2-9.k^2+32.k^2=108\)
\(\Rightarrow\left(4-9+32\right).k^2=108\)
\(\Rightarrow27.k^2=108\)
\(\Rightarrow k^2=4\)
\(\Rightarrow k=\pm2\)
+) \(k=2\Rightarrow a=4,b=6,d=8\)
+) \(k=-2\Rightarrow a=-4,b=-6,c=-8\)
Vậy bộ số \(\left(a;b;c\right)\) là \(\left(4;6;8\right);\left(-4;-6;-8\right)\)
Đúng 0
Bình luận (0)
ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}nên\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}\)
và a2-b2+2c2=108
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}=\frac{a^2-b^2+2c^2}{4-9+32}=\frac{108}{27}=4\)
=> a2=16; b2=36; c2=64
=> a=4; b=6; c=8
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm a,b,c biết
a) 2a=3b;5b=7c và 3a+5c-7b=30
b)\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}và\)\(a^2-b^2+2c^2=108\)
c)\(\frac{a}{3}=\frac{b+1}{4}=\frac{c+2}{5}và\)\(a-b+c=-17\)
CÁC BÀI NÀY ĐỀU GIẢI THEO TÍNH CHẤT DÃY TỈ SỐ BẮNG NHAU
a) ta có: 2a = 3b; 5b = 7c
\(\Rightarrow\frac{a}{3}=\frac{b}{2};\frac{b}{7}=\frac{c}{5}\)
\(\Rightarrow\frac{a}{21}=\frac{b}{14}\left(1\right);\frac{b}{14}=\frac{c}{10}\left(2\right)\)
VẾ (1) nhân cả 2 số với\(\frac{1}{7}\); VẾ (2) nhân cả hai số với \(\frac{1}{2}\)
\(\Rightarrow\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)
\(\Rightarrow\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}\)
ÁP DỤNG T/C DÃY TỈ SỐ BẰNG NHAU, TA CÓ:
\(\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}=\frac{3a+5c-7b}{63+50-98}=\frac{30}{15}=2\)
PHẦN SAU TỰ LÀM^-^
c) ÁP DỤNG T/C DÃY TỈ SỐ BẰNG NHAU TA CÓ:
\(\frac{a}{3}=\frac{b+1}{4}=\frac{c+2}{5}=\frac{a-b-1+c+2}{3-4+5}=\frac{a-b+c+1}{4}=\frac{-17}{4}\)
PHẦN SAU TỰ LÀM^-^
Đúng 0
Bình luận (0)
Tìm a,b,c biết:
a)\(\frac{a}{5}=\frac{b}{4}\)và\(a^2-b^2=1\)
b)\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)và \(a^2-b^2+2c^2=108\)
\(\frac{a}{5}=\frac{b}{4}\\ \Rightarrow\frac{a^2}{25}=\frac{b^2}{16}=\frac{a^2-b^2}{25-16}=\frac{1}{9}\\ \Rightarrow a^2=\frac{25}{9}\\ \Rightarrow a=\frac{5}{3}\)
tự tính b nhé
b) Câu b tương tự câu a .
Nếu ko biết hỏi mình
Đúng 0
Bình luận (2)
a)\(\frac{a}{5}=\frac{b}{4}\) và a2-b2=1
\(\Rightarrow\left(\frac{a}{5}\right)^2=\left(\frac{b}{4}\right)^2\Rightarrow\frac{a^2}{25}=\frac{b^2}{16}\Rightarrow\frac{a^2}{25}=\frac{b^2}{16}=\frac{a^2-b^2}{25-16}=\frac{1}{9}\)(T/C...)
\(\Rightarrow a^2=\frac{25}{9}\Rightarrow a=\pm\frac{5}{3}\)
\(\Rightarrow b^2=\frac{16}{9}\Rightarrow b=\pm\frac{4}{3}\)
Vậy cặp số (a;b) là \(\left(\frac{5}{3};\frac{4}{3}\right),\left(-\frac{5}{3},-\frac{4}{3}\right)\)
Đúng 0
Bình luận (0)
a) tìm a,b,c biết \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\) và a + 2b - 3c = -20
b) tìm m,n,p biết \(\frac{m}{2}=\frac{n}{3}=\frac{p}{4}\) và m2 - n2 +2p2 = 108
\(a,\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\Rightarrow\frac{a}{2}=\frac{2b}{6}=\frac{3c}{12}\)
\(\Leftrightarrow\frac{a+2b-3c}{2+6-12}=\frac{-20}{-4}=5\)
Vậy: \(a=5.2=10\)
\(b=5.6:2=15\)
\(c=5.12:3=20\)
Đúng 0
Bình luận (0)
sao con gai ma de anh con trai vay cau trac nghich lam nhi
Đúng 0
Bình luận (0)
b, Ta có :
\(\frac{m}{2}=\frac{n}{3}=\frac{p}{4}=\frac{m^2}{4}=\frac{n^2}{9}=\frac{p^2}{16}\)
\(\Rightarrow\frac{m^2}{4}=\frac{n^2}{9}=\frac{2p^2}{32}=\frac{m^2-n^2+2p^2}{4-9+32}=\frac{108}{27}=4\)
Do đó :
\(\frac{m^2}{4}=4\Leftrightarrow m^2=16\Leftrightarrow m=\pm4\)
\(\frac{n^2}{9}=4\Leftrightarrow n^2=36\Leftrightarrow n=\pm6\)
\(\frac{2p^2}{32}=4\Leftrightarrow2p^2=128\Leftrightarrow p^2=64\Leftrightarrow p=\pm8\)
Vậy : ...
Đúng 0
Bình luận (0)
Tìm 2 số a,b biết:
a) \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}và,a^2-b^2+2c^2=108\)





























