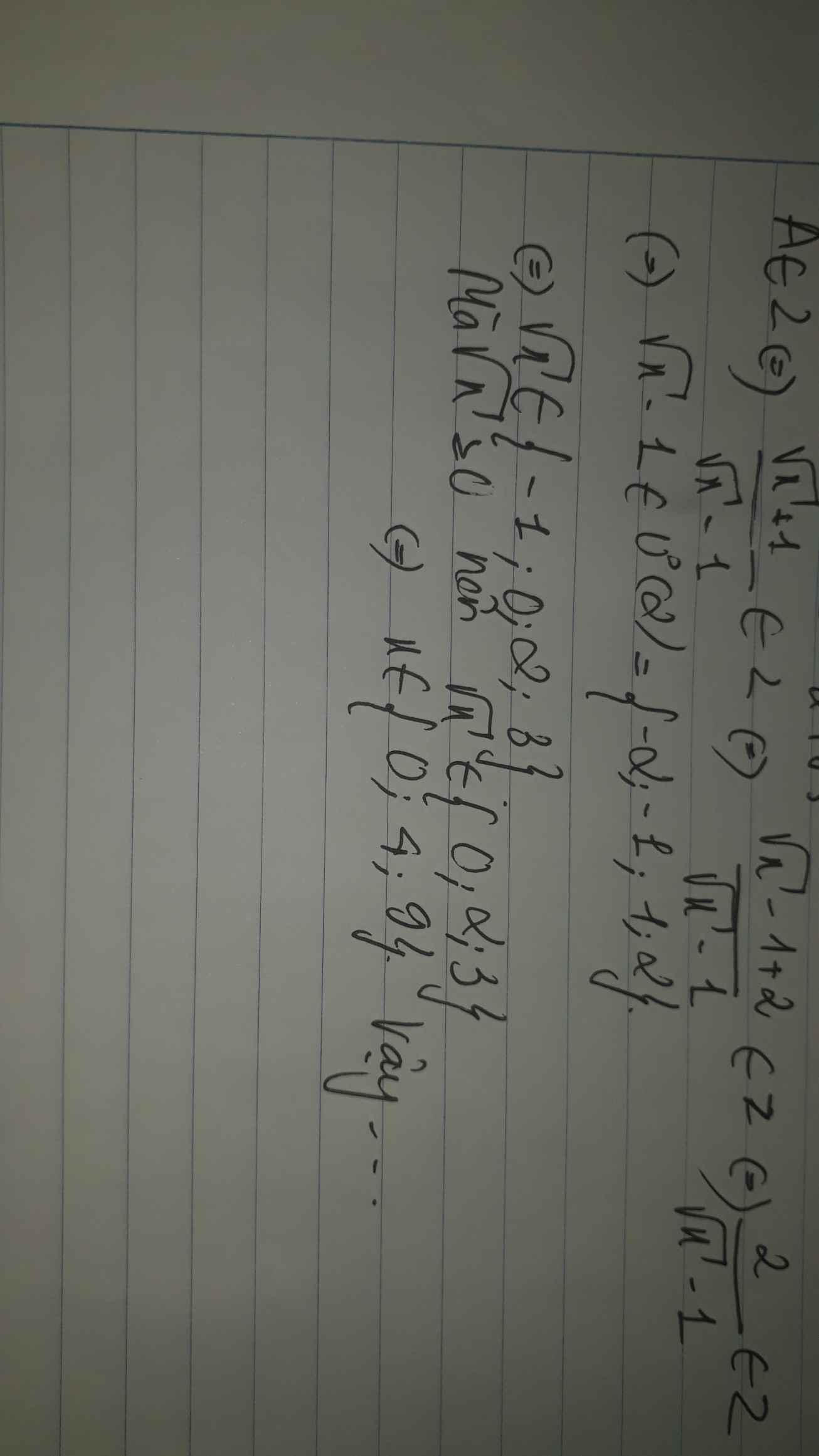Giúp em chi tiết bài này vs 

Những câu hỏi liên quan
Giúp em chi tiết bài này vs 
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{2}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)
Để \(A\in Z\) thì \(\sqrt{x}-1\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)
Mà \(x\in Z,x\ge0,x\ne1\)
\(\Rightarrow x\in\left\{4;0;9\right\}\)
Đúng 0
Bình luận (0)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow2⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
hay \(x\in\left\{0;4;9\right\}\)
Đúng 0
Bình luận (0)
Giúp em giải chi tiết bài này vs ạ
\(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)\)
Để \(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}< 0\) thì
\(\sqrt{x}-3< 0\) ( do \(\sqrt{x}+3\ge3>0\))
\(\Leftrightarrow\sqrt{x}< 3\Leftrightarrow0\le x< 9\)
Mà \(x\in Z\)
\(\Rightarrow x\in\left\{0;1;2;3;4;5;6;7;8\right\}\)
Đúng 2
Bình luận (0)
Để M là số nguyên âm thì \(\sqrt{x}-3< 0\)
\(\Leftrightarrow\sqrt{x}< 3\)
hay \(x\in\left\{0;1;4\right\}\)
Đúng 1
Bình luận (0)
 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Giúp em chi tiết câu này vs 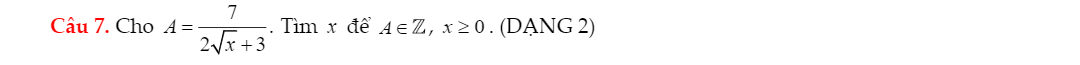
Lời giải:
Dễ thấy $2\sqrt{x}+3>0; 7>0$ nên $A>0$
Mặt khác:
$2\sqrt{x}\geq 0\Rightarrow 2\sqrt{x}+3\geq 3$
$\Rightarrow A=\frac{7}{2\sqrt{x}+3}\leq \frac{7}{3}$
Vậy $0< A< \frac{7}{3}$
$A\in\mathbb{Z}\Leftrightarrow A\in\left\{1;2\right\}$
$\Leftrightarrow \frac{7}{2\sqrt{x}+3}\in \left\{1;2\right\}$
$\Leftrightarrow x\in\left\{4; \frac{1}{16}\right\}$
Đúng 0
Bình luận (0)
Để A là số nguyên thì \(7⋮2\sqrt{x}+3\)
\(\Leftrightarrow2\sqrt{x}+3=7\)
\(\Leftrightarrow2\sqrt{x}=4\)
hay x=4
Đúng 0
Bình luận (0)

 giải chi tiết 3 bài này dùm em vs ạ
giải chi tiết 3 bài này dùm em vs ạ
em cảm ơn mọi người nhiều
Giúp em chi tiết bài này

a, Ta có : \(AB//CD\)
\(\Rightarrow\dfrac{AB}{DC}=\dfrac{IB}{ID}=\dfrac{IA}{IC}\)
\(\Rightarrow\Delta IAB\sim\Delta ICD\)
b, Ta có : \(\left\{{}\begin{matrix}IM//DC\\IN//DC\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{IM}{DC}=\dfrac{AI}{AC}\\\dfrac{IN}{DC}=\dfrac{BI}{BD}\end{matrix}\right.\)
Mà \(\dfrac{IA}{IC}=\dfrac{IB}{ID}\) \(\Rightarrow\dfrac{AI}{AC}=\dfrac{BI}{BD}\)
\(\Rightarrow\dfrac{IM}{DC}=\dfrac{IN}{DC}\)
\(\Rightarrow IM=IN\)
c, CMTT câu b ta được KI đi qua chung điểm của AB và CD .
Đúng 1
Bình luận (0)
Giúp mình chi tiết bài này vs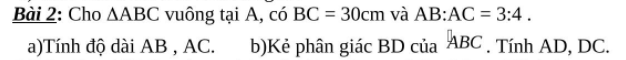
đừng chép mạng nha , tự làm giùm mình vs
a): ta có AB^2 + AC^2 = 30^2 = 900 <=> AB = √(900 - AC^2)
AB:AC = 3:4 <=> AB = 3 * AC / 4
=> √(900 - AC^2) = 3 * AC / 4
<=> 900 - AC^2 = 9 * AC^2 / 16
<=> 14400 - 16 * AC^2 = 9 * AC^2
<=> 14400 = 25 * AC^2
<=> 576 = AC^2
<=> AC = 24
=> AB = 24 / 4 * 3 = 18
Đúng 0
Bình luận (1)
b): Áp dụng định lý tia phân giác trong tam giác ta có BA / BC = DA / DC
=> DA / DC = 3 / 4 <=> DA = 3 * DC / 4
mà DA + DC = AC = 24 <=> DA = 24 - DC
=> 3 * DC / 4 = 24 - DC
<=> 96 - 4 * DC = 3 * DC
<=> 96 = 7 * DC
<=> DC = 96 / 7
=> DA = 24 - 96/7 = 72 / 7
Đúng 0
Bình luận (0)
Giúp em chi tiết bài này với

Bài 4:
a) Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+BH^2=AB^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2=15^2-12^2=81\)
hay BH=9(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{AH^2}{HB}=\dfrac{12^2}{9}=16\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AC^2}=\dfrac{1}{12^2}-\dfrac{1}{15^2}=\dfrac{1}{400}\)
hay AC=20(cm)
Vậy: BH=9cm; CH=16cm; AC=20cm
Đúng 0
Bình luận (1)
b) Xét ΔCFE và ΔCAB có
\(\dfrac{CF}{CA}=\dfrac{CE}{CB}\left(\dfrac{4}{20}=\dfrac{5}{25}\right)\)
\(\widehat{C}\) chung
Do đó: ΔCFE∼ΔCAB(c-g-c)
Suy ra: \(\widehat{CFE}=\widehat{CAB}\)(hai góc tương ứng)
mà \(\widehat{CAB}=90^0\)(ΔABC cân tại A)
nên \(\widehat{CFE}=90^0\)
hay ΔCFE vuông tại F
c) Ta có: \(\dfrac{CF}{CA}=\dfrac{CE}{CB}\left(\dfrac{4}{20}=\dfrac{5}{25}\right)\)
nên \(CE\cdot CA=CF\cdot CB\)(đpcm)
Đúng 0
Bình luận (0)
Giúp em chi tiết bài này với 
a: Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=180^0\)
Do đó: AFHE là tứ giác nội tiếp
Xét tứ giác BFHD có
\(\widehat{BFH}+\widehat{BDH}=180^0\)
Do đó: BFHD là tứ giác nội tiếp
Xét tứ giác ECDH có
\(\widehat{HEC}+\widehat{HDC}=180^0\)
Do đó: ECDH là tứ giác nội tiếp
b: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Xét tứ giác CDFA có
\(\widehat{CDA}=\widehat{CFA}=90^0\)
Do đó: CDFA là tứ giác nội tiếp
Đúng 0
Bình luận (0)