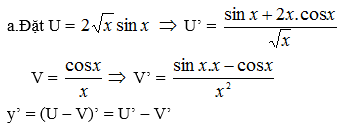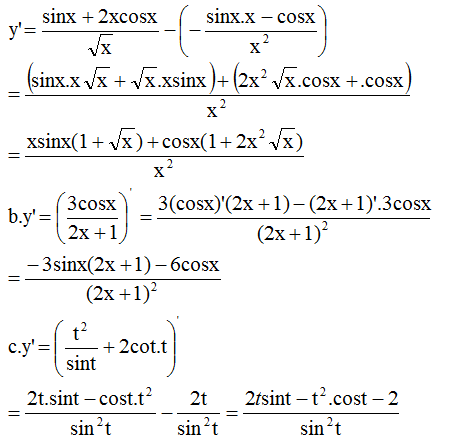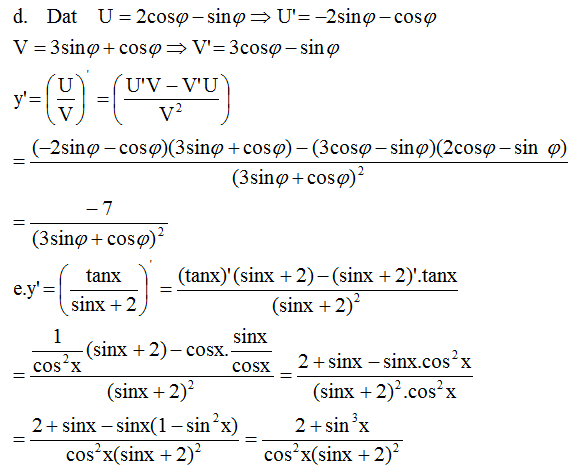a.

\(y=\dfrac{3}{2}sin2x-2\left(cos^2x-sin^2x\right)+5=\dfrac{3}{2}sin2x-2cos2x+5\)

\(=\dfrac{5}{2}\left(\dfrac{3}{5}sin2x-\dfrac{4}{5}cos2x\right)+5=\dfrac{5}{2}sin\left(2x-a\right)+5\) (với \(cosa=\dfrac{3}{5}\))

\(\Rightarrow-\dfrac{5}{2}+5\le y\le\dfrac{5}{2}+5\)

b.

\(\Leftrightarrow y.sinx-2y.cosx+4y=3sinx-cosx+1\)

\(\Leftrightarrow\left(y-3\right)sinx+\left(1-2y\right)cosx=1-4y\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất:

\(\left(y-3\right)^2+\left(1-2y\right)^2\ge\left(1-4y\right)^2\)

\(\Leftrightarrow11y^2+2y-9\le0\)

\(\Leftrightarrow-1\le y\le\dfrac{9}{11}\)

c.

Do \(x^2+y^2=1\Rightarrow\) đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)

\(\Rightarrow y=\dfrac{2\left(sin^2a+6sina.cosa\right)}{1+2sina.cosa+cos^2a}=\dfrac{1-cos2a+6sin2a}{1+sin2a+\dfrac{1+cos2a}{2}}=\dfrac{2-2cos2a+12sin2a}{3+2sin2a+cos2a}\)

\(\Leftrightarrow3y+2y.sin2a+y.cos2a=2-2cos2a+12sin2a\)

\(\Leftrightarrow\left(2y-12\right)sin2a+\left(y+2\right)cos2a=2-3y\)

Theo điều kiện có nghiệm của pt bậc nhất theo sin2a, cos2a:

\(\left(2y-12\right)^2+\left(y+2\right)^2\ge\left(2-3y\right)^2\)

\(\Leftrightarrow y^2+8y-36\le0\)

\(\Rightarrow-4-2\sqrt{13}\le y\le-4+2\sqrt{13}\)

a: \(y=\sqrt{2}sin\left(x+\dfrac{pi}{4}\right)\)

\(-1< =sin\left(x+\dfrac{pi}{4}\right)< =1\)

=>\(-\sqrt{2}< =y< =\sqrt{2}\)

\(y_{min}=-\sqrt{2}\) khi sin(x+pi/4)=-1

=>x+pi/4=-pi/2+k2pi

=>x=-3/4pi+k2pi

\(y_{max}=\sqrt{2}\) khi sin(x+pi/4)=1

=>x+pi/4=pi/2+k2pi

=>x=pi/4+k2pi

b: \(y=sinx\cdot cos\left(\dfrac{pi}{3}\right)+cosx\cdot sin\left(\dfrac{pi}{3}\right)+3\)

\(=sin\left(x+\dfrac{pi}{3}\right)+3\)

-1<=sin(x+pi/3)<=1

=>-1+3<=sin(x+pi/3)+3<=4

=>2<=y<=4

y min=2 khi sin(x+pi/3)=-1

=>x+pi/3=-pi/2+k2pi

=>x=-5/6pi+k2pi

y max=4 khi sin(x+pi/3)=1

=>x+pi/3=pi/2+k2pi

=>x=pi/6+k2pi

c: \(y=2\cdot\left(sin2x\cdot\dfrac{\sqrt{3}}{2}-cos2x\cdot\dfrac{1}{2}\right)\)

\(=2sin\left(2x-\dfrac{pi}{6}\right)\)

-1<=sin(2x-pi/6)<=1

=>-2<=y<=2

y min=-2 khi sin(2x-pi/6)=-1

=>2x-pi/6=-pi/2+k2pi

=>2x=-1/3pi+k2pi

=>x=-1/6pi+kpi

y max=2 khi sin(2x-pi/6)=1

=>2x-pi/6=pi/2+k2pi

=>2x=2/3pi+k2pi

=>x=1/3pi+kpi

a) Cách 1: Ta có:

y' = 6sin⁵x.cosx - 6cos⁵x.sinx + 6sinx.cos³x - 6sin³x.cosx = 6sin³x.cosx(sin²x - 1) + 6sinx.cos³x(1 - cos²x) = - 6sin³x.cos³x + 6sin³x.cos³x = 0.

Vậy y' = 0 với mọi x, tức là y' không phụ thuộc vào x.

Cách 2:

y = sin⁶x + cos⁶x + 3sin²x.cos²x(sin²x + cos²x) = sin⁶x + 3sin⁴x.cos²x + 3sin²x.cos⁴x + cos⁶x = (sin²x + cos²x)³ = 1

Do đó, y' = 0.

b) Cách 1:

Áp dụng công thức tính đạo hàm của hàm số hợp

(cos²u)' = 2cosu(-sinu).u' = -u'.sin2u

Ta được

y' =[sin - sin] + [sin - sin] - 2sin2x = 2cos.sin(-2x) + 2cos.sin(-2x) - 2sin2x = sin2x + sin2x - 2sin2x = 0,

vì cos = cos = .

Vậy y' = 0 với mọi x, do đó y' không phụ thuộc vào x.

Cách 2: vì côsin của hai cung bù nhau thì đối nhau cho nên

cos² = cos² '

cos² = cos² .

Do đó

y = 2 cos² + 2cos² - 2sin²x = 1 +cos + 1 +cos - (1 - cos2x) = 1 +cos + cos + cos2x = 1 + 2cos.cos(-2x) + cos2x = 1 + 2cos2x + cos2x = 1.

Do đó y' = 0.

Câu 1:

\(y=S\left(\frac{3-S^2}{2}\right)=\frac{3}{2}S-\frac{1}{2}S^3\)

Khi \(S\rightarrow+\infty\) thì \(y\rightarrow-\infty\)

Khi \(S\rightarrow-\infty\) thì \(y\rightarrow+\infty\)

Hàm số không có GTLN và GTNN

Câu 2:

\(y=sin^4x+cos^4x+2sin^2x.cos^2x-2sin^2x.cos^2x\)

\(y=\left(sin^2x+cos^2x\right)^2-\frac{1}{2}\left(2sinx.cosx\right)^2\)

\(y=1-\frac{1}{2}sin^22x\)

Do \(0\le sin^22x\le1\)

\(\Rightarrow y_{max}=1\) khi \(sin2x=0\)

\(y_{min}=\frac{1}{2}\) khi \(sin2x=\pm1\)

Câu 3:

\(y=sin^6x+cos^6x+3sin^2x.cos^2x\left(sin^2x+cos^2x\right)-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\)

\(y=\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\)

\(y=1-\frac{3}{4}sin^22x\)

Do \(0\le sin^22x\le1\)

\(\Rightarrow y_{max}=1\) khi \(sin2x=0\)

\(y_{min}=\frac{1}{4}\) khi \(sin2x=\pm1\)

Câu 4:

\(y=\frac{cosx+2sinx+3}{2cosx-sinx+4}\)

\(\Leftrightarrow2y.cosx-y.sinx+4y=cosx+2sinx+3\)

\(\Leftrightarrow\left(y+2\right)sinx+\left(1-2y\right)cosx=4y-3\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất:

\(\left(y+2\right)^2+\left(1-2y\right)^2\ge\left(4y-3\right)^2\)

\(\Leftrightarrow11y^2-24y+4\le0\)

\(\Leftrightarrow\frac{2}{11}\le y\le2\)

Yêu cầu đề bài là gì vậy bạn?

a.

Tìm min:

$y=(4\sin ^2x-4\sin x+1)+2=(2\sin x-1)^2+2$
Vì $(2\sin x-1)^2\geq 0$ với mọi $x$ nên $y=(2\sin x-1)^2+2\geq 0+2=2$

Vậy $y_{\min}=2$

----------------

Mặt khác: 

$y=4\sin x(\sin x+1)-8(\sin x+1)+11$

$=(\sin x+1)(4\sin x-8)+11$

$=4(\sin x+1)(\sin x-2)+11$

Vì $\sin x\in [-1;1]\Rightarrow \sin x+1\geq 0; \sin x-2<0$

$\Rightarrow 4(\sin x+1)(\sin x-2)\leq 0$

$\Rightarrow y=4(\sin x+1)(\sin x-2)+11\leq 11$

Vậy $y_{\max}=11$

b.

$y=\cos ^2x+2\sin x+2=1-\sin ^2x+2\sin x+2$

$=3-\sin ^2x+2\sin x$
$=4-(\sin ^2x-2\sin x+1)=4-(\sin x-1)^2\leq 4-0=4$

Vậy $y_{\max}=4$.

---------------------------

Mặt khác:

$y=3-\sin ^2x+2\sin x = (1-\sin ^2x)+(2+2\sin x)$

$=(1-\sin x)(1+\sin x)+2(1+\sin x)=(1+\sin x)(1-\sin x+2)$

$=(1+\sin x)(3-\sin x)$

Vì $\sin x\in [-1;1]$ nên $1+\sin x\geq 0; 3-\sin x>0$

$\Rightarrow y=(1+\sin x)(3-\sin x)\geq 0$

Vậy $y_{\min}=0$

c.

$y=\sin ^4x-2\cos ^2x+1=\sin ^4x-2(1-\sin ^2x)+1$

$=\sin ^4x+2\sin ^2x-1$

$=(\sin ^4x-1)+(2\sin ^2x-2)+2$

$=(\sin ^2x-1)(\sin ^2x+1)+2(\sin ^2x-1)+2$

$=(\sin ^2x-1)(\sin ^2x+3)+2$

Vì $\sin x\in [-1;1]$ nên $\sin ^2x\leq 1$

$\Rightarrow (\sin ^2x-1)(\sin ^2x+3)\leq 0$

$\Rightarrow y=(\sin ^2x-1)(\sin ^2x+3)+2\leq 2$

Vậy $y_{\max}=2$

------------------------------------------

$y=\sin ^4x+2\sin ^2x-1=\sin ^2x(\sin ^2x+2)-1$

Vì $\sin ^2x\geq 0$ nên $\sin ^2x(\sin ^2x+2)\geq 0$

$\Rightarrow y=\sin ^2x(\sin ^2x+2)-1\geq 0-1=-1$
Vậy $y_{\min}=-1$