Xác định dạng của tam giác ABC và tính S:
A(3;1) B(-1;-3) C(2;-4)
xác định dạng của tam giác ABC biết a,AB=15cm; AC=20cm; BC=25cm b, AB=4cm; BC=4√(2); AC=4cm
a, Vì AB2+AC2=152+202=625 cm
BC2=252=625 cm
=> AB2+AC2=BC2 => tg ABC vuông tại A
b, Ta có AB2+AC2=32 cm
BC2=32 cm
=> AB2+AC2=BC2 => tg ABC vuông tại A
Mà AB=AC=4cm
=> tg ABC vuông cân tại A
Cho tam giác ABC. Xét mệnh đề dạng \(P \Rightarrow Q\) như sau:
“Nếu tam giác ABC vuông tại A thì tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)”.
Phát biểu mệnh đề \(Q \Rightarrow P\) và xác định tính đúng sai của hai mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\).
P: “tam giác ABC vuông tại A”
Q: “tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)”
+) Mệnh đề \(Q \Rightarrow P\) là “Nếu tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)thì tam giác ABC vuông tại A”
+) Từ định lí Pytago, ta có:
Tam giác ABC vuông tại A thì \(A{B^2} + A{C^2} = B{C^2}\)
Và: Tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\) thì vuông tại A.
Do vậy, hai mệnh đề “\(P \Rightarrow Q\)” và “\(Q \Rightarrow P\)” đều đúng.
Bài 3: Xác định dạng của tam giác ABC trong mỗi trường hợp sau:
a) AB=AC
b) AC=BC và góc A bằng 60 độ.
a: ΔABC cân tại A
b: ΔABC đều
\(1. Cho tam giác ABC cân tại A,gọi D và E là Trung điểm của AB và AC. a, Xác định dạng của tứ giác DBEC b, Cho biết BD=8 cm. Tính DE\)
Xét tam giác ABC có:
D là trung điểm của AB
E là trung điểm của AC
=>DE là đường trung bình của tam giác ABC
=>DE//BC
=>tứ giác DBEC là hình thang
Vì tam giác ABC cân tại A
=>AB=AC
=>AD=BD=AE=AC ( D là trung điểm AB,E là trung điểm AC )
mà BD=8cm =>AE=8cm
a, Xét tam giác ABC có :
D là trung điểm của AB
E là trung điểm của AC
Nên : DE // BC (*)
Suy ra : DE là đường trung bình của tam giác ABC
Do đó : Tứ giác DBEC là hình thang
Từ (*) ⇒ Góc ADE = Góc ABC ( sole trong )
⇒ Góc AED = Góc ACB ( sole trong )
Lại có : Góc ABC = Góc ACB ( △ ABC cân tại A )
Nên : Góc ADE = Góc AED
Suy ra : △ ADE cân tại A
Do đó : AD = AE ( 2 cạnh bên )
Mà : AD = BD ( D là trung điểm của AB )
AE = CE ( E là trung điểm của AC )
Nên : BD = CE
Vậy hình thang DBEC là hình thang cân.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M trên tia đối của tia CB lấy điểm N sao cho BM = CN
Khi góc BAC = 60o và BM = CN = BC hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC
Khi góc BAC = 60º và BM = CN = BC
Tam giác cân ABC có góc BAC = 60º nên là tam giác đều
⇒ AB = BC và góc B1 = 60º
Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒ 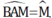
Mà theo tính chất góc ngoài trong ΔBAM thì
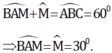
Tương tự ta có
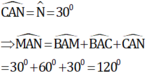
* Ta chứng minh tam giác OBC là tam giác đều.
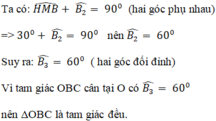
Cho tam giác ABC có góc A bàng 60độ góc B bằng 70độ D va E lần lượt là trung điểm của AB, AC . Xác định dạng tứ giác BDCE và tính các góc của nó
cho tam giác ABC , phân giác góc B cắt phân giác góc ngoài của góc A tại D hãy xác định dạng của tam giác ABC biết tam giác ABD cân tại A
Vi goc BAE =goc EAD
suy ra AE la tia phan giac cua goc BAD
vi tam giac BAD la tam giac can tai A
suy ra goc ABD= goc ADB ,AEcuungla duong trung tuyen suy ra BE=ED
MA ABD=DBC
Suy ra ADB=BDC
Xet hai tam giac EBC va tam giac EDA co
AED=BEC(DOI DINH)
BE=ED(cmt)
DBC=ADE(cmt)
suy ra Hai tam giac tren bang nhau (g.c.g)
Suy ra BC=AD9hai cnh tuong ung)
Vay tam giac ABC la tam giac can
Bai nay con nhieu cach chung minh khac nhung ma thoi gian khong ch phep minh chi lam mot cach nay thoi
Cho tam giác ABC ,ở phái ngoài tam giác vẽ các tam giác vuông cân tại A là ABD,ACE .Hãy xác định định dạng của tam giác ABC . Biết rằng BD = CE
giúp mk vs bn nào lm nhanh và đúng mk tick cho :))
Tam giác ABC có Â=60, B=70. D và E theo thứ tự là trung điểm của AB và AC. Xác định dạng tứ giác BDEC và tính các góc của nó ?
:D
quá dễ chỉ tai vì mày nghiện magan thôi