Gieo 5 lần một con xúc xắc. Tính xác suất để trong 5 lần gieo đó có 3 lần xuất hiện mặt 6 chấm.

Những câu hỏi liên quan
a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng bao nhiêu?
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng bao nhiêu?
a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng: \(\dfrac{5}{11}\)
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng: \(\dfrac{3}{14}\)
Đúng 2
Bình luận (0)
Gieo một con xúc xắc 2 lần liên tiếp, có 7 lần xuất hiện mặt 5 chấm. Tính xác suất thực nghiệm xuất hiện 5 chấm
Xem chi tiết
a)nếu gieo 1 xúc xắc 21 lần liên tiếp, có 5 lần xuất hiện mặt 5 chấm thì xác suất thực nghiệm mặt 5 chấm là bao nhiêu???
b)nếu gieo 1 xúc xắc 17 lần liên tiếp, có 4 lần liên tiếp xuất hiện mặt 1 chấm thì xác suất thực nghiệm xuất hiện mặt 1 chấm là bao nhiêu???
chệu lun á khó quấ
Gieo một con xúc xắc 2 lần. Xác suất để mặt 6 chấm không xuất hiện là A.
25
36
.
B.
11
36
.
C.
1
6
.
D.
2
9
.
Đọc tiếp
Gieo một con xúc xắc 2 lần. Xác suất để mặt 6 chấm không xuất hiện là
A. 25 36 .
B. 11 36 .
C. 1 6 .
D. 2 9 .
Đáp án A
Số phần tử của không gian mẫu: n Ω = 6 .6 = 36 .
Gọi A là biến cố mặt 6 chấm không xuất hiện.
Khi đó n A = 5 .5 = 25 ⇒ P A = n A n Ω = 25 36 .
Đúng 0
Bình luận (0)
Gieo một con xúc xắc 2 lần. Xác suất để mặt 6 chấm không xuất hiện là A. B. C. D.
Đọc tiếp
Gieo một con xúc xắc 2 lần. Xác suất để mặt 6 chấm không xuất hiện là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố mặt 6 chấm không xuất hiện.
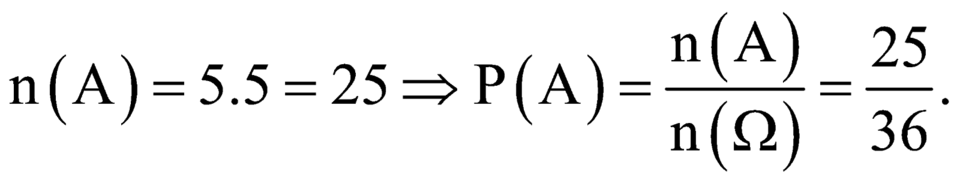
Đúng 0
Bình luận (0)
gieo một con xúc xắc hai lần liên tiếp. tính xác suất trong các trường hợp a. lần gieo thứ nhất xuất hiện mặt một chấm b. tổng số chấm hai lần gieo bằng 5 c. hiệu số chấm hai lần gieo bằng 2 d. tích số chấm hai lần gieo là một số lẻ e. tổng số chấm hai lần gieo là một số chia hết cho 3
a: A={(1;1); (1;2); ...; (1;6)}
=>n(A)=6
P(A)=6/36=1/6
b: B={(1;4); (2;3); (3;2); (4;1)}
=>P(B)=4/36=1/9
c: C={(3;1); (4;2); (5;3); (6;4)}
=>P(C)=4/36=1/9
d: D={(1;3); (1;5); (1;1); (3;5); (3;1); (3;3); (5;3); (5;1); (5;5)}
=>P(D)=9/36=1/4
Đúng 1
Bình luận (0)
Gieo một con xúc xắc 3 lần. Tính xác suất để tổng số chấm xuất hiện ở 3 lần gieo là một số chẵn
Nếu gieo một con xúc xắc 10 lần liên tiếp có 4 lần xuất hiện mặt 5 chấm thì xác suất thực nghiệm xuất hiện mặt 5 chấm là: Nêu cách trình bày
cách trình bày là
Tổng số lần gieo xúc sắc là:
n=10(lần)
Tổng số lần gieo được 5 chấm là:
K=4(lần)
XSTH của sự kiện xuất hiện mặt 5 chấm là:
\(\dfrac{K}{n}\)=\(\dfrac{4}{10}\)=\(\dfrac{2}{5}\)
Đúng 0
Bình luận (1)
Gieo một xúc xắc hai lần liên tiếp. Tính xác suất của mỗi biến cố sau:a) A : Lần thứ hai xuất hiện mặt 5 chấm;b) B : Tổng số chấm xuất hiện trong hai lần gieo bằng 7 ;c) C: Tổng số chấm xuất hiện trong hai lần gieo chia hết cho 3;d) D : Số chấm xuất hiện lần thứ nhất là số nguyên tố;e) E: Số chấm xuất hiện lần thứ nhất nhỏ hơn số chấm xuất hiện lần thứ hai.
Đọc tiếp
Gieo một xúc xắc hai lần liên tiếp. Tính xác suất của mỗi biến cố sau:
a) A : "Lần thứ hai xuất hiện mặt 5 chấm";
b) B : "Tổng số chấm xuất hiện trong hai lần gieo bằng 7 ";
c) C: "Tổng số chấm xuất hiện trong hai lần gieo chia hết cho 3";
d) D : "Số chấm xuất hiện lần thứ nhất là số nguyên tố";
e) E: "Số chấm xuất hiện lần thứ nhất nhỏ hơn số chấm xuất hiện lần thứ hai".
a: n(omega)=36
A={(1;5); (2;5); (3;5); (4;5); (5;5); (6;5)}
=>n(A)=6
=>P(A)=6/36=1/6
b: B={(1;6); (2;5); (3;4); (4;3); (5;2); (6;1)}
=>n(B)=6
=>P(B)=1/6
d: D={(2;1); (2;2); ...; (2;6); (3;1); (3;2); ...;(3;6);(5;1); (5;2);...;(5;6)}
=>P(D)=18/36=1/2
Đúng 1
Bình luận (0)
















