Chứng minh rằng :
\(\sqrt{\dfrac{3}{\sqrt[3]{32}+\sqrt[3]{16}+3}}=\sqrt[3]{4}-1\)
Cho \(x=\dfrac{\sqrt{2}-1}{1+2}+\dfrac{\sqrt{3}-\sqrt{2}}{2+3}+\dfrac{\sqrt{4}-\sqrt{3}}{3+4}+...+\dfrac{\sqrt{225}-\sqrt{224}}{224+225}\) . Chứng minh rằng \(x< \dfrac{7}{15}\) .
Chứng minh rằng số x0=\(\sqrt{2+\sqrt{2+\sqrt{3}}}-\sqrt{6-3\sqrt{2+\sqrt{3}}}\)là 1 nghiệm của pt x\(x^4+16^2+32=0\)
chứng minh rằng:\(\dfrac{1}{3\left(\sqrt{1}+\sqrt{2}\right)}+\dfrac{1}{5\left(\sqrt{2}+\sqrt{3}\right)}+\dfrac{1}{7\left(\sqrt{3}+\sqrt{4}\right)}+...+\dfrac{1}{97\left(\sqrt{48}+\sqrt{49}\right)}< \dfrac{3}{7}\)
Bạn tham khảo câu số 9:
chứng minh rằng với số tự nhiên n,n lớn hơn 4 ta có:
\(\dfrac{1}{2\sqrt{1}+1\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+\dfrac{1}{4\sqrt{3}+3\sqrt{4}}+...+\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}< 1\)
\(\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\dfrac{\left(n+1\right)\sqrt{n}-n\sqrt{n+1}}{\left(n+1\right)^2n-n^2\left(n+1\right)}\)
\(=\dfrac{\left(n+1\right)\sqrt{n}-n\sqrt{n+1}}{n\left(n+1\right)}=\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\)
Do đó:
\(VT=\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\)
\(VT=1-\dfrac{1}{\sqrt{n+1}}< 1\) (đpcm)
Bài 1 : \(a)\) Chứng minh : \(cos15^o=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
\(b)\) Trục căn thức của biểu thức : \(A=\dfrac{1}{2+\sqrt[3]{2}+\sqrt[3]{32.cos^415^o-10-8\sqrt{3}}}\)
Bài 1 :
a) \(Cos30^o=Cos\left(2.15^o\right)=2cos^215^o-1\)
\(\Rightarrow cos^215^o=\dfrac{cos30^o+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\dfrac{\sqrt[]{3}}{2}+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\sqrt[]{3}+2}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\sqrt[]{3}+2}}{2}\)
\(\Rightarrow cos15^o=\dfrac{2\sqrt[]{\sqrt[]{3}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{4\sqrt[]{3}+8}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6+2.2\sqrt[]{2}\sqrt[]{6}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\left(\sqrt[]{6}+\sqrt[]{2}\right)^2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6}+\sqrt[]{2}^{ }}{4}\left(dpcm\right)\)
a)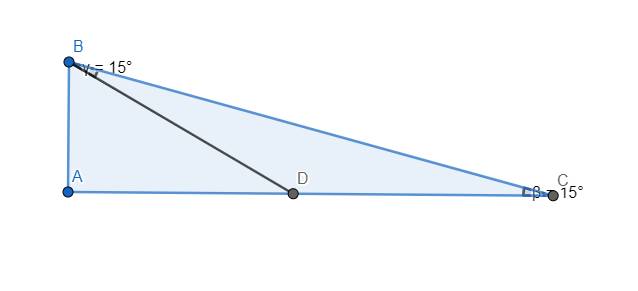
Dựng tam giác ABC vuông tại A với \(\widehat{C}=15^o\). Trên đoạn thẳng AC lấy điểm D sao cho \(\widehat{CBD}=15^o\). Không mất tính tổng quát, ta chuẩn hóa \(AB=1\). \(\Rightarrow\left\{{}\begin{matrix}BD=\dfrac{AB}{cos60^o}=2\\AD=AB.tan60^o=\sqrt{3}\end{matrix}\right.\)
Dễ thấy tam giác DBC cân tại D \(\Rightarrow BD=CD=2\) \(\Rightarrow AC=AD+DC=2+\sqrt{3}\)
\(\Rightarrow tanC=\dfrac{AB}{AC}=\dfrac{1}{2+\sqrt{3}}=2-\sqrt{3}\)
\(\Rightarrow\dfrac{sinC}{cosC}=2-\sqrt{3}\)
\(\Rightarrow sinC=\left(2-\sqrt{3}\right)cosC\)
Mà \(sin^2C+cos^2C=1\)
\(\Rightarrow\left(7-4\sqrt{3}\right)cos^2C+cos^2C=1\)
\(\Leftrightarrow\left(8-4\sqrt{3}\right)cos^2C=1\)
\(\Leftrightarrow cos^2C=\dfrac{1}{8-4\sqrt{3}}=\dfrac{2+\sqrt{3}}{4}\)
\(\Leftrightarrow cosC=\sqrt{\dfrac{2+\sqrt{3}}{4}}\) \(=\dfrac{\sqrt{2+\sqrt{3}}}{2}=\dfrac{\sqrt{8+4\sqrt{3}}}{4}\) \(=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
b) \(A=\dfrac{1}{2+\sqrt[3]{2}+\sqrt[3]{32cos^415^o-10-8\sqrt[]{3}}}\)
\(\Rightarrow A=\dfrac{1}{2+\sqrt[3]{2}+\sqrt[3]{32.\dfrac{1}{4^4}\left(\sqrt[]{6}+\sqrt[]{2}\right)^4-10-8\sqrt[]{3}}}\) \(\left(Cos15^o=\dfrac{\sqrt[]{6}-\sqrt[]{2}}{4}\right)\)
\(\Rightarrow A=\dfrac{1}{2+\sqrt[3]{2}+\sqrt[3]{\dfrac{1}{8}\left(8+2\sqrt[]{12}\right)^2-10-8\sqrt[]{3}}}\)
\(\Rightarrow A=\dfrac{1}{2+\sqrt[3]{2}+\sqrt[3]{\dfrac{1}{8}\left[64+32\sqrt[]{12}+48-80-64\sqrt[]{3}\right]}}\)
\(\Rightarrow A=\dfrac{1}{2+\sqrt[3]{2}+\dfrac{1}{2}\sqrt[3]{32}}\)
\(\Rightarrow A=\dfrac{1}{2+\sqrt[3]{2}+\dfrac{1}{2}.2\sqrt[3]{4}}=\dfrac{1}{2+\sqrt[3]{2}+\sqrt[3]{4}}\)
1) Chứng minh rằng : \(\dfrac{1}{\sqrt{1}+\sqrt{2}}\) +\(\dfrac{1}{\sqrt{3}+\sqrt{4}}\)+....+\(\dfrac{1}{\sqrt{79}+\sqrt{80}}\) >4
\(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}...+\dfrac{1}{\sqrt{79}+\sqrt{80}}\)
\(=\left(\sqrt{2}-\sqrt{1}\right)+\left(\sqrt{3}-\sqrt{2}\right)+...+\left(\sqrt{80}-\sqrt{79}\right)\)
\(=\sqrt{80}-\sqrt{2}\)
Đến đây bấm máy rồi đối chiếu kết quả cho nhanh, hoặc nếu em thik "màu mè" hơn thì giả sử lớn hơn rồi biến đổi tương đương thôi :)
1) Chứng minh rằng: \(1+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{3\sqrt{3}}+...+\dfrac{1}{n\sqrt{n}}< 2\sqrt{2}\left(n\in N\right)\)
2) Chứng minh rằng: \(\dfrac{2}{3}+\sqrt{n+1}< 1+\sqrt{2}+\sqrt{3}+...+\sqrt{n}< \dfrac{2}{3}\left(n+1\right)\sqrt{n}\)
3) \(2\sqrt{n}-3< \dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{n}}< 2\sqrt{n}-2\)
4) \(\dfrac{\sqrt{2}-\sqrt{1}}{2+1}+\dfrac{\sqrt{3}-\sqrt{2}}{3+2}+...+\dfrac{\sqrt{n+1}-\sqrt{n}}{n+1+n}< \dfrac{1}{2}\left(1-\dfrac{1}{\sqrt{n+1}}\right)\)
Bài 40: Chứng minh rằng:
a) \(A=\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+...+\dfrac{1}{\sqrt{99}+\sqrt{100}}=9\)
b) \(B=\dfrac{1}{2\sqrt{1}+1\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+\dfrac{1}{4\sqrt{3}+3\sqrt{4}}+...+\dfrac{1}{100\sqrt{99}+99\sqrt{100}}=\dfrac{9}{10}\)
Cho biểu thức : P= \(\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2}{x-4}\right).\left(\sqrt{x}-1+\dfrac{\sqrt{x}-4}{\sqrt{x}}\right)\) (với x>0; x\(\ne\)4)
1) Chứng minh rằng P=\(\sqrt{x}\)+3
2) Tìm các giá trị của x sao cho P=x+3
`1)P((\sqrtx+1)/(\sqrtx-2)-2/(x-4)).(\sqrtx-1+(\sqrtx-4)/\sqrtx)(x>0,x ne 4)`
`=((x+3\sqrtx+2-2)/(x-4)).((x-\sqrtx+\sqrtx-4)/\sqrtx)`
`=((x+3\sqrtx-4)/(x-4)).((x-4)/\sqrtx))`
`=(x+3\sqrtx)/\sqrtx`
`=(\sqrtx(\sqrtx+3))/\sqrtx`
`=\sqrtx+3(đpcm)`
`2)P=x+3
`<=>\sqrtx+3=x+3`
`<=>x-\sqrtx=0`
`<=>\sqrtx(\sqrtx-1)=0`
Vì `x>0=>\sqrtx>0`
`=>\sqrtx-1=0<=>x=1(tm)`
Vậy `x=1=>\sqrtx+3=x+3`
`1)P((\sqrtx+1)/(\sqrtx-2)-2/(x-4)).(\sqrtx-1+(\sqrtx-4)/\sqrtx)(x>0,x ne 4)`
`=((x+3\sqrtx+2-2)/(x-4)).((x-\sqrtx+\sqrtx-4)/\sqrtx)`
`=((x+3\sqrtx)/(x-4)).((x-4)/\sqrtx))`
`=(x+3\sqrtx)/\sqrtx`
`=(\sqrtx(\sqrtx+3))/\sqrtx`
`=\sqrtx+3(đpcm)`
`2)P=x+3
`<=>\sqrtx+3=x+3`
`<=>x-\sqrtx=0`
`<=>\sqrtx(\sqrtx-1)=0`
Vì `x>0=>\sqrtx>0`
`=>\sqrtx-1=0<=>x=1(tm)`
Vậy `x=1=>\sqrtx+3=x+3`