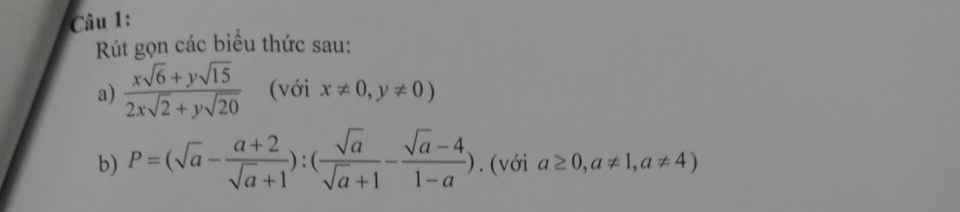Bài 7:
Ta có: \(C=\dfrac{4+\sqrt{7}}{3\sqrt{2}+\sqrt{4+\sqrt{7}}}+\dfrac{4-\sqrt{7}}{3\sqrt{2}-\sqrt{4-\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{6+\sqrt{8+2\sqrt{7}}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{6-\sqrt{8-2\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{7+\sqrt{7}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{7-\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{7}-1\right)\left(4+\sqrt{7}\right)}{6\sqrt{7}}+\dfrac{\sqrt{2}\left(\sqrt{7}+1\right)\left(4-\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(-3+3\sqrt{7}+3+3\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\sqrt{2}\)
6.
Ta có:
\(A=\sqrt{20+\sqrt{20+...+\sqrt{20}}}>\sqrt{20+\sqrt{\dfrac{1}{16}}}=\dfrac{9}{2}\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}>\sqrt[3]{24}=\sqrt[3]{\dfrac{192}{8}}>\sqrt[3]{\dfrac{125}{8}}=\dfrac{5}{2}\)
\(\Rightarrow A+B>\dfrac{9}{2}+\dfrac{5}{2}=7\)
\(A=\sqrt[]{20+\sqrt[]{20+...+\sqrt[]{20}}}< \sqrt[]{20+\sqrt[]{20+...+\sqrt[]{25}}}=5\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}< \sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{27}}}=3\)
\(\Rightarrow A+B< 5+3=8\)
8.
Ta có:
\(a=\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}-\dfrac{\sqrt{2}}{8}\Rightarrow\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}=a+\dfrac{\sqrt{2}}{8}\)
\(a^2=\dfrac{1}{4}\left(\sqrt{2}+\dfrac{1}{8}\right)+\dfrac{1}{32}-\dfrac{\sqrt{2}}{4}.\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}\)
\(=\dfrac{\sqrt{2}}{4}+\dfrac{1}{32}+\dfrac{1}{32}-\dfrac{\sqrt{2}}{4}\left(a+\dfrac{\sqrt{2}}{8}\right)\)
\(=\dfrac{\sqrt{2}}{4}+\dfrac{1}{16}-\dfrac{\sqrt{2}}{4}a-\dfrac{1}{16}\)
\(=\dfrac{\sqrt{2}}{4}\left(1-a\right)\)
\(\Rightarrow a^4=\dfrac{1}{8}\left(a^2-2a+1\right)\)
\(\Rightarrow a^4+a+1=\dfrac{1}{8}\left(a^2-2a+1\right)+a+1=\dfrac{1}{8}\left(a+3\right)^2\)
\(\Rightarrow R=a^2+\dfrac{\sqrt{2}}{4}\left(a+3\right)=\dfrac{\sqrt{2}}{4}\left(1-a\right)+\dfrac{\sqrt{2}}{4}\left(a+3\right)=\sqrt{2}\)
9.
Xét \(a_n=\dfrac{1}{\left(2a+1\right)\left(\sqrt{a}+\sqrt{a+1}\right)}=\dfrac{\sqrt{a+1}-\sqrt{a}}{2a+1}< \dfrac{1}{2}\left(\dfrac{1}{\sqrt{a}}-\dfrac{1}{\sqrt{a+1}}\right)\)
\(\Rightarrow S< \dfrac{1}{2}\left(\dfrac{1}{1}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{48}}-\dfrac{1}{\sqrt{49}}\right)\)
\(\Rightarrow S< \dfrac{1}{2}\left(1-\dfrac{1}{7}\right)=\dfrac{3}{7}\)
Vậy \(S< \dfrac{3}{7}\)


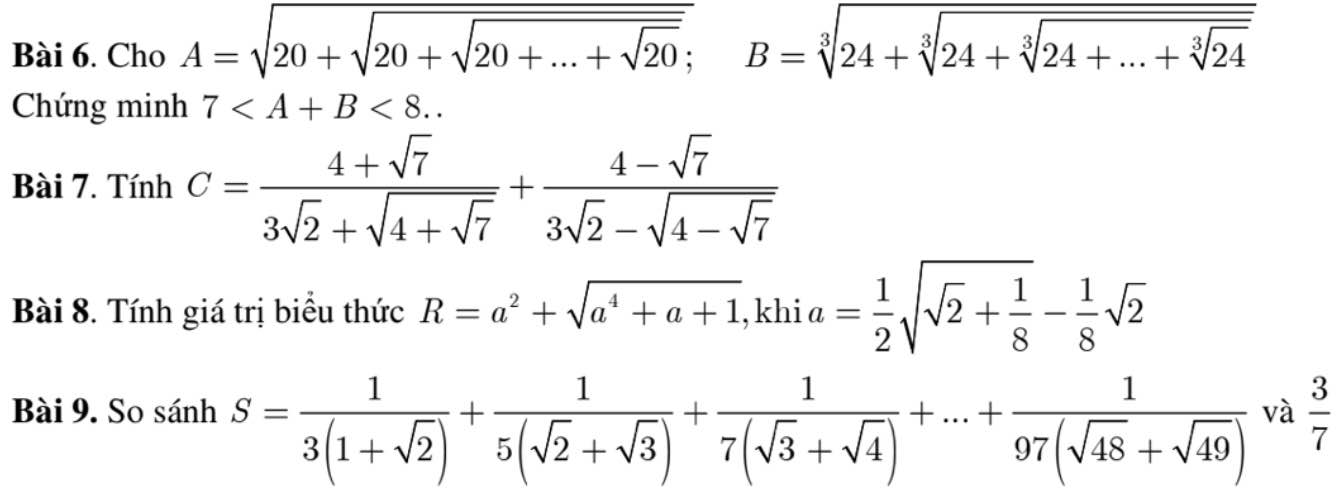











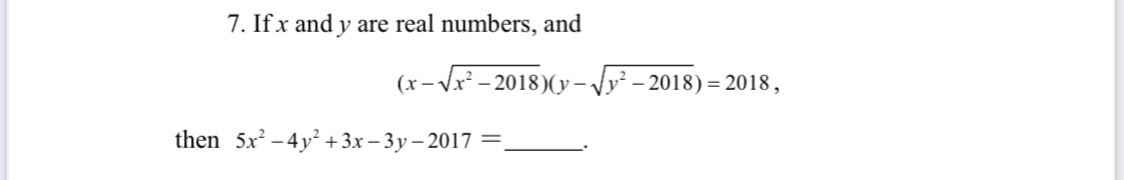

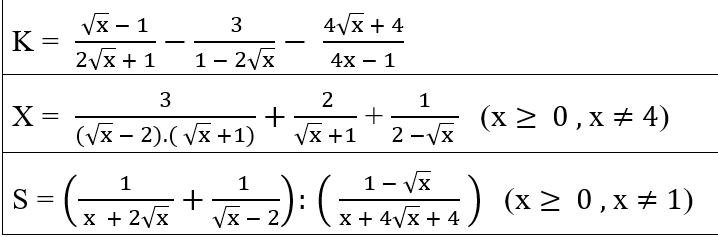

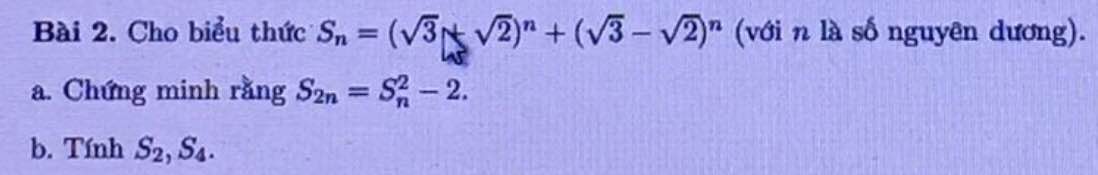 mọi người giải giúp em bài này với ạ 🥺
mọi người giải giúp em bài này với ạ 🥺